人教版七年级下册7.2.2 用坐标表示平移 课件(共29张)
文档属性
| 名称 | 人教版七年级下册7.2.2 用坐标表示平移 课件(共29张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 09:06:45 | ||
图片预览








文档简介
(共29张PPT)
用坐标表示平移
复习旧知 引入新课
问题:还记得什么叫做平移吗?平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动叫做平移.
平移后图形的位置改变,形状、大小不变.
复习旧知 引入新课
想一想
图形平移,图形的形状、大小不变,但位置发生了变化,图形上点的坐标也随着发生了怎样的变化呢?
探究发现
()
()
问题
()如图,将点()向右平移个单位长度,得到点.
探究发现 归纳总结
()
()
问题
()如图,将点()向右平移个单位长度,得到点,在图上标出它的坐标,观察坐标的变化,你能从中发现什么规律吗?
问题
()如图,将点()向右平移个单位长度,得到点,在图上标出它的坐标,观察坐标的变化,你能从中发现什么规律吗?把点向上平移个单位长度呢
()
探究发现 归纳总结
()
()
探究发现 归纳总结
点()向右平移个单位长度,得到点,它的坐标是___________.
观察点、点的坐标可以发现:点的横坐标等于点的横坐标___________.
点的纵坐标________点A的纵坐标.
点()向上平移个单位长度,得到点,它的坐标是___________.
观察点、点的坐标可以发现:点的横坐标_______点的横坐标.
点的纵坐标等于点的纵坐标___________.
()
加
等于
等于
()
加
问题
()把点()向左或向下平移个单位长度,观察坐标的变化,你能从中发现什么规律吗?
()
()
把点向左平移个单位长度,横坐标________,纵坐标__________.
把点向下平移个单位长度,横坐标________,纵坐标__________.
减
不变
不变
减
探究发现 归纳总结
()
()
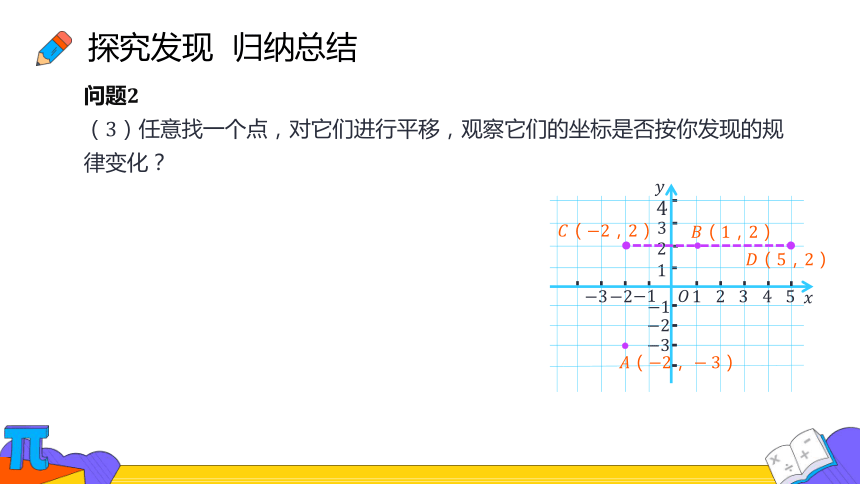
问题
()任意找一个点,对它们进行平移,观察它们的坐标是否按你发现的规律变化?
()
()
探究发现 归纳总结
()
()
()
问题
()任意找一个点,对它们进行平移,观察它们的坐标是否按你发现的规律变化?
()
左右平移,_____坐标不变, ______坐标右_____左______.
纵
横
加
减
探究发现 归纳总结
()
()
上下平移,_____坐标不变, ______坐标右_____左______.
横
纵
加
减
()
说说点或图形的平移能引起坐标怎样的变化规律?
探究发现 归纳总结
在平面直角坐标系中,
()将点(,)向右(或向左)平移个单位长度,可以得到对应的的坐标是____________或____________.
()将点(,)向上(或向下)平移个单位长度,可以得到对应的的坐标是____________或____________.
(,)
(,)
(,)
(,)
问题
问题:如图,正方形四个顶点的坐标分别是(),(),(),().
问题
问题:如图,正方形四个顶点的坐标分别是(),(),(),(),将正方形向下平移个单位长度,再向右平移个单位长度,两次平移后四个顶点相应变化为.
()点坐标分别是什么?
问题
()
()
()
()
向右平移8个单位长度
向下平移7个单位长度
()
()
()
()
问题
问题:如图,正方形四个顶点的坐标分别是(),(),(),(),将正方形向下平移个单位长度,再向右平移个单位长度,两次平移后四个顶点相应变化为.
()如果直接平移正方形,使点移到点,它和我们前面得到的正方形位置相同吗?
问题
()
()
()
()
()
()
()
()
问题
解:平移正方形,使点移到点,它和我们前面得到的正方形位置相同.
问题:如图,三个顶点的坐标分别是:(),(),().
()将三个顶点的横坐标都减去,纵坐标不变,分别得到点,
点分别是什么?并画出相应的.
探究发现
()
()
()
问题:如图,三个顶点的坐标分别是:(),(),().
()与的大小、形状和位置上有什么关系,为什么?
探究发现
,与的大小、形状完全相同.
问题:如图,三个顶点的坐标分别是:(),(),().
()若顶点的横坐标都加,纵坐标不变呢?
探究发现
用类比的思想,把三个顶点的横坐标都加,纵坐标不变.
问题:如图,三个顶点的坐标分别是:(),(),().
()若顶点的横坐标都加,纵坐标不变呢?
探究发现
用类比的思想,把三个顶点的横坐标都加,纵坐标不变. 右平移了个单位长度,因此得到的三角形与△ 的大小、形状完全相同.
问题:如图,三个顶点的坐标分别是:(),(),().
()若顶点的纵坐标都减去,横坐标不变.
猜想: 2与的大小、形状和位置上有什么关系?
探究发现
用类比的思想,可得2与的大小、形状完全相同,可以看作将向下平移个单位长度.
问题: ()如图,将三个顶点的横坐标都减去,同时纵坐标减去,又能得到什么结论?其中(),(),().
探究发现
将的三个顶点的横坐标都减去,同时纵坐标减去,分别得到对应点坐标记作( ),( ),( ).
,
,
,
问题: ()如图,将三个顶点的横坐标都减去,同时纵坐标减去,又能得到什么结论?其中(),(),().
探究发现
依次连接这三点,可以发现可以由向左平移个单位长度,再向下平移个单位长度得到.
问题: ()如图,将三个顶点的横坐标都减去,同时纵坐标减去,又能得到什么结论?其中(),(),().
探究发现
依次连接这三点,可以发现可以由向左平移个单位长度,再向下平移个单位长度得到. 两三角形的大小、形状完全相同.
理解深化 归纳总结
通过前面问题的探究,你能总结图形上点的坐标的某种变化引起了图形怎样的平移吗?
在平面直角坐标系内,
如果把一个图形各个点的横坐标都加(或减去)一个正数,
相应的新图形就是把原图形_______(或_______)平移个单位长度;
如果把它各个点的纵坐标都加(或减去)一个正数,
相应的新图形就是把原图形_______(或_______)平移个单位长度;
向右
向左
向上
向下
课堂小结
课堂小结
1.点或图形的平移引起点的坐标怎样的变化规律?
左右平移,纵坐标不变,横坐标右加左减.
上下平移,横坐标不变,纵坐标上加下减.
2.图形上点的坐标的某种变化引起了图形怎样的平移?
横坐标加减,纵坐标不变,横坐标加向右,横坐标减向左.
纵坐标加减,横坐标不变,纵坐标加向上,纵坐标减向下.
再 见
用坐标表示平移
复习旧知 引入新课
问题:还记得什么叫做平移吗?平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动叫做平移.
平移后图形的位置改变,形状、大小不变.
复习旧知 引入新课
想一想
图形平移,图形的形状、大小不变,但位置发生了变化,图形上点的坐标也随着发生了怎样的变化呢?
探究发现
()
()
问题
()如图,将点()向右平移个单位长度,得到点.
探究发现 归纳总结
()
()
问题
()如图,将点()向右平移个单位长度,得到点,在图上标出它的坐标,观察坐标的变化,你能从中发现什么规律吗?
问题
()如图,将点()向右平移个单位长度,得到点,在图上标出它的坐标,观察坐标的变化,你能从中发现什么规律吗?把点向上平移个单位长度呢
()
探究发现 归纳总结
()
()
探究发现 归纳总结
点()向右平移个单位长度,得到点,它的坐标是___________.
观察点、点的坐标可以发现:点的横坐标等于点的横坐标___________.
点的纵坐标________点A的纵坐标.
点()向上平移个单位长度,得到点,它的坐标是___________.
观察点、点的坐标可以发现:点的横坐标_______点的横坐标.
点的纵坐标等于点的纵坐标___________.
()
加
等于
等于
()
加
问题
()把点()向左或向下平移个单位长度,观察坐标的变化,你能从中发现什么规律吗?
()
()
把点向左平移个单位长度,横坐标________,纵坐标__________.
把点向下平移个单位长度,横坐标________,纵坐标__________.
减
不变
不变
减
探究发现 归纳总结
()
()
问题
()任意找一个点,对它们进行平移,观察它们的坐标是否按你发现的规律变化?
()
()
探究发现 归纳总结
()
()
()
问题
()任意找一个点,对它们进行平移,观察它们的坐标是否按你发现的规律变化?
()
左右平移,_____坐标不变, ______坐标右_____左______.
纵
横
加
减
探究发现 归纳总结
()
()
上下平移,_____坐标不变, ______坐标右_____左______.
横
纵
加
减
()
说说点或图形的平移能引起坐标怎样的变化规律?
探究发现 归纳总结
在平面直角坐标系中,
()将点(,)向右(或向左)平移个单位长度,可以得到对应的的坐标是____________或____________.
()将点(,)向上(或向下)平移个单位长度,可以得到对应的的坐标是____________或____________.
(,)
(,)
(,)
(,)
问题
问题:如图,正方形四个顶点的坐标分别是(),(),(),().
问题
问题:如图,正方形四个顶点的坐标分别是(),(),(),(),将正方形向下平移个单位长度,再向右平移个单位长度,两次平移后四个顶点相应变化为.
()点坐标分别是什么?
问题
()
()
()
()
向右平移8个单位长度
向下平移7个单位长度
()
()
()
()
问题
问题:如图,正方形四个顶点的坐标分别是(),(),(),(),将正方形向下平移个单位长度,再向右平移个单位长度,两次平移后四个顶点相应变化为.
()如果直接平移正方形,使点移到点,它和我们前面得到的正方形位置相同吗?
问题
()
()
()
()
()
()
()
()
问题
解:平移正方形,使点移到点,它和我们前面得到的正方形位置相同.
问题:如图,三个顶点的坐标分别是:(),(),().
()将三个顶点的横坐标都减去,纵坐标不变,分别得到点,
点分别是什么?并画出相应的.
探究发现
()
()
()
问题:如图,三个顶点的坐标分别是:(),(),().
()与的大小、形状和位置上有什么关系,为什么?
探究发现
,与的大小、形状完全相同.
问题:如图,三个顶点的坐标分别是:(),(),().
()若顶点的横坐标都加,纵坐标不变呢?
探究发现
用类比的思想,把三个顶点的横坐标都加,纵坐标不变.
问题:如图,三个顶点的坐标分别是:(),(),().
()若顶点的横坐标都加,纵坐标不变呢?
探究发现
用类比的思想,把三个顶点的横坐标都加,纵坐标不变. 右平移了个单位长度,因此得到的三角形与△ 的大小、形状完全相同.
问题:如图,三个顶点的坐标分别是:(),(),().
()若顶点的纵坐标都减去,横坐标不变.
猜想: 2与的大小、形状和位置上有什么关系?
探究发现
用类比的思想,可得2与的大小、形状完全相同,可以看作将向下平移个单位长度.
问题: ()如图,将三个顶点的横坐标都减去,同时纵坐标减去,又能得到什么结论?其中(),(),().
探究发现
将的三个顶点的横坐标都减去,同时纵坐标减去,分别得到对应点坐标记作( ),( ),( ).
,
,
,
问题: ()如图,将三个顶点的横坐标都减去,同时纵坐标减去,又能得到什么结论?其中(),(),().
探究发现
依次连接这三点,可以发现可以由向左平移个单位长度,再向下平移个单位长度得到.
问题: ()如图,将三个顶点的横坐标都减去,同时纵坐标减去,又能得到什么结论?其中(),(),().
探究发现
依次连接这三点,可以发现可以由向左平移个单位长度,再向下平移个单位长度得到. 两三角形的大小、形状完全相同.
理解深化 归纳总结
通过前面问题的探究,你能总结图形上点的坐标的某种变化引起了图形怎样的平移吗?
在平面直角坐标系内,
如果把一个图形各个点的横坐标都加(或减去)一个正数,
相应的新图形就是把原图形_______(或_______)平移个单位长度;
如果把它各个点的纵坐标都加(或减去)一个正数,
相应的新图形就是把原图形_______(或_______)平移个单位长度;
向右
向左
向上
向下
课堂小结
课堂小结
1.点或图形的平移引起点的坐标怎样的变化规律?
左右平移,纵坐标不变,横坐标右加左减.
上下平移,横坐标不变,纵坐标上加下减.
2.图形上点的坐标的某种变化引起了图形怎样的平移?
横坐标加减,纵坐标不变,横坐标加向右,横坐标减向左.
纵坐标加减,横坐标不变,纵坐标加向上,纵坐标减向下.
再 见
