人教版七年级下册8.1 二元一次方程组 课件(共20张)
文档属性
| 名称 | 人教版七年级下册8.1 二元一次方程组 课件(共20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 09:13:16 | ||
图片预览






文档简介
(共20张PPT)
人教版数学七年级下册
8.1二元一次方程组
只含有一个未知数
未知数的次数都是1
等号两边都是整式
使方程左、右两边相等的未知数的值,叫做方程的解。
1、什么是一元一次方程?
2、什么是方程的解?
温故知新
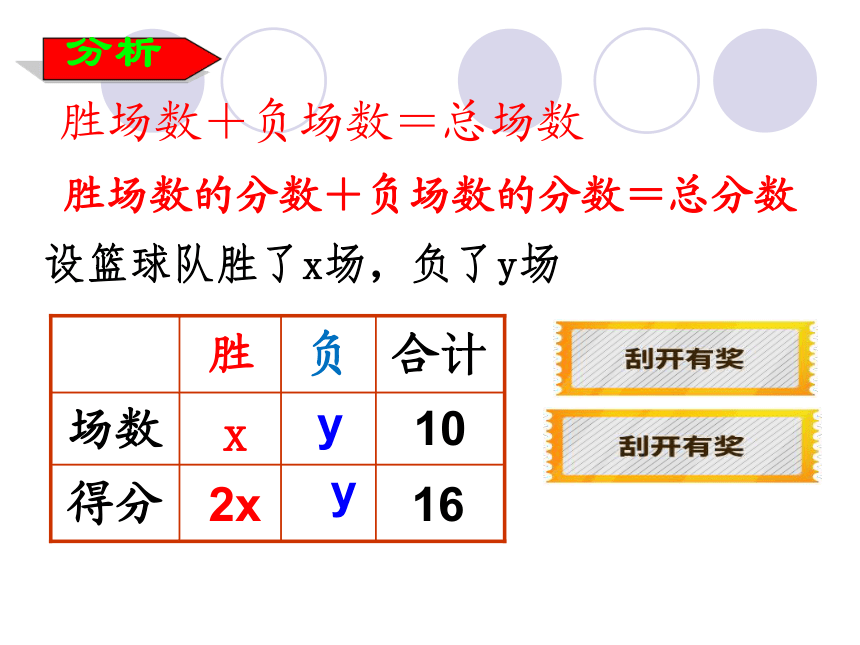
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.如果某队为了争取较好名次,想在全部10场比赛中得16分,那么这个队胜负场数分别是多少
解:设胜x场、则负(10-x)场.
问题
胜的场数+负的场数=总场数
胜场积分+负场积分=总积分
分析:
2x+(10-x)=16
分析
胜场数+负场数=总场数
胜场数的分数+负场数的分数=总分数
设篮球队胜了x场,负了y场
得分
10
场数
合计
负
胜
x
y
2x
y
16
2x+y=16
x+y=10
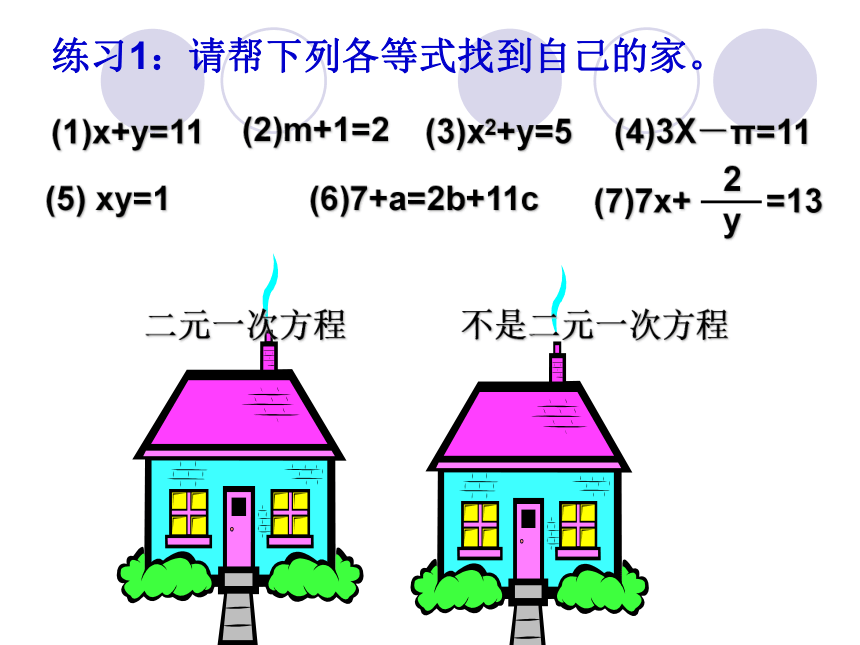
含有两个未知数,并且所含未知数的项的次数都是1次的整式方程叫做二元一次方程.
知识点1、二元一次方程
(1)上面每个方程有什么特点
(2)与一元一次方程比较有什么区别
(3)猜想一下它们是什么方程
思考:
二元一次方程
不是二元一次方程
(1)x+y=11
(3)x2+y=5
(2)m+1=2
(4)3X-π=11
(5) xy=1
(6)7+a=2b+11c
(7)7x+ =13
y
2
练习1:请帮下列各等式找到自己的家。
就组成了一个方程组.
把方程x+y=10 和2x+y=16合在一起写成
x+y=10
2x+y=16
(1)这个方程组含有几个未知数?
(2)含有未知数的项的次数是多少?
(3)共有几个整式方程?
思考:
知识点2、二元一次方程组
含有 个未知数,每个未知数的项的次数都是 ,并且一共有 个方程,像这样的方程组叫做二元一次方程组.
2
1
两
下列哪些是二元一次方程组?并说明理由。
(1) x+y= 2 (2) x+ = 1
x-y=1 x = y
(3) x=0 (4) z=x+1
y=1 2x-y=5
(5) x-3y=8 (6) 3x=5y
xy=6 2x-y=0
y
1
(是)
(是)
(不是)
(不是)
(是)
(不是)
二元一次方程组:
一共有两个方程
组中有两个未知数
含每个未知数的项的次数都是1
④整式方程
满足方程x+y=10且符合实际意义的x,y的值有哪些?
知识点3、二元一次方程的解
10
0
0
1
2
3
4
5
6
7
8
9
y
10
9
8
7
6
5
4
3
2
1
x
使二元一次方程两边的值相等的两个未知数的值叫做二元一次方程的解.
满足方程2x+y=16且符合实际意义的x,y的值有哪些?
16
0
0
2
4
6
8
10
12
14
y
8
7
6
5
4
3
2
1
x
二元一次方程的解和一元一次方程的解有什么区别?
一元一次方程的解 二元一次方程的解
一个
无数个
一个未知数的值
一对未知数的值
结论:二元一次方程有无数个解。
议一议
10
0
0
1
2
3
4
5
6
7
8
9
y
10
9
8
7
6
5
4
3
2
1
x
16
0
0
2
4
6
8
10
12
14
y
8
7
6
5
4
3
2
1
x
x+y=10与2x+y=16的公共解是哪一个
6
4
6
4
的解.
把
叫做二元一次方程组
X=6
y =4
x+y=10
2x+y=16
知识点4、二元一次方程组的解
二元一次方程组的两个方程的公共解叫做二元一次方程组的解
1.下列各组数中______是方程x-3y=2的解. _______是方程2x-y=9的解.
X=-1
y=-1
A:
B:
X=5
y =1
C:
X=3
y =2
D:
y =-5
X=2
2.方程组
x-3y=2
2x-y=9
的解是上面的( )
A、
B
B、
D
B
练一练:
二元一次方程(组)
二元一次方程概念
二元一次方程组的概念
二元一次方程的解
二元一次方程组的解
知识树
会检验二元一次方程组的解
会检验二元一次方程的解
分享你我收获
1、若x2m-1+5y3n =7是二元一次方程,则m=_ ,n=_ .
2、已知 是方程2x-4y+3a=3的一组解,则a=
1
1
X=2
X=1
巩固提升:
若(x-5)2+∣2x+3y∣=0,则求x、y的值?
解得:
X-5=0
2x+3y=0
中考链接:
1、课本89页练习。
2、已知x+2y=-5,用含y的式子表示x是 ,用含x的式子表示y是 .
作业:
如果一个长方形的周长为20cm,长为x cm,宽为y cm.
(1)请列出方程,并判断是否为二元一次方程.
(2)当x=6时,求y的值.
拓展训练:
THANK YOU!
感谢聆听
人教版数学七年级下册
8.1二元一次方程组
只含有一个未知数
未知数的次数都是1
等号两边都是整式
使方程左、右两边相等的未知数的值,叫做方程的解。
1、什么是一元一次方程?
2、什么是方程的解?
温故知新
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.如果某队为了争取较好名次,想在全部10场比赛中得16分,那么这个队胜负场数分别是多少
解:设胜x场、则负(10-x)场.
问题
胜的场数+负的场数=总场数
胜场积分+负场积分=总积分
分析:
2x+(10-x)=16
分析
胜场数+负场数=总场数
胜场数的分数+负场数的分数=总分数
设篮球队胜了x场,负了y场
得分
10
场数
合计
负
胜
x
y
2x
y
16
2x+y=16
x+y=10
含有两个未知数,并且所含未知数的项的次数都是1次的整式方程叫做二元一次方程.
知识点1、二元一次方程
(1)上面每个方程有什么特点
(2)与一元一次方程比较有什么区别
(3)猜想一下它们是什么方程
思考:
二元一次方程
不是二元一次方程
(1)x+y=11
(3)x2+y=5
(2)m+1=2
(4)3X-π=11
(5) xy=1
(6)7+a=2b+11c
(7)7x+ =13
y
2
练习1:请帮下列各等式找到自己的家。
就组成了一个方程组.
把方程x+y=10 和2x+y=16合在一起写成
x+y=10
2x+y=16
(1)这个方程组含有几个未知数?
(2)含有未知数的项的次数是多少?
(3)共有几个整式方程?
思考:
知识点2、二元一次方程组
含有 个未知数,每个未知数的项的次数都是 ,并且一共有 个方程,像这样的方程组叫做二元一次方程组.
2
1
两
下列哪些是二元一次方程组?并说明理由。
(1) x+y= 2 (2) x+ = 1
x-y=1 x = y
(3) x=0 (4) z=x+1
y=1 2x-y=5
(5) x-3y=8 (6) 3x=5y
xy=6 2x-y=0
y
1
(是)
(是)
(不是)
(不是)
(是)
(不是)
二元一次方程组:
一共有两个方程
组中有两个未知数
含每个未知数的项的次数都是1
④整式方程
满足方程x+y=10且符合实际意义的x,y的值有哪些?
知识点3、二元一次方程的解
10
0
0
1
2
3
4
5
6
7
8
9
y
10
9
8
7
6
5
4
3
2
1
x
使二元一次方程两边的值相等的两个未知数的值叫做二元一次方程的解.
满足方程2x+y=16且符合实际意义的x,y的值有哪些?
16
0
0
2
4
6
8
10
12
14
y
8
7
6
5
4
3
2
1
x
二元一次方程的解和一元一次方程的解有什么区别?
一元一次方程的解 二元一次方程的解
一个
无数个
一个未知数的值
一对未知数的值
结论:二元一次方程有无数个解。
议一议
10
0
0
1
2
3
4
5
6
7
8
9
y
10
9
8
7
6
5
4
3
2
1
x
16
0
0
2
4
6
8
10
12
14
y
8
7
6
5
4
3
2
1
x
x+y=10与2x+y=16的公共解是哪一个
6
4
6
4
的解.
把
叫做二元一次方程组
X=6
y =4
x+y=10
2x+y=16
知识点4、二元一次方程组的解
二元一次方程组的两个方程的公共解叫做二元一次方程组的解
1.下列各组数中______是方程x-3y=2的解. _______是方程2x-y=9的解.
X=-1
y=-1
A:
B:
X=5
y =1
C:
X=3
y =2
D:
y =-5
X=2
2.方程组
x-3y=2
2x-y=9
的解是上面的( )
A、
B
B、
D
B
练一练:
二元一次方程(组)
二元一次方程概念
二元一次方程组的概念
二元一次方程的解
二元一次方程组的解
知识树
会检验二元一次方程组的解
会检验二元一次方程的解
分享你我收获
1、若x2m-1+5y3n =7是二元一次方程,则m=_ ,n=_ .
2、已知 是方程2x-4y+3a=3的一组解,则a=
1
1
X=2
X=1
巩固提升:
若(x-5)2+∣2x+3y∣=0,则求x、y的值?
解得:
X-5=0
2x+3y=0
中考链接:
1、课本89页练习。
2、已知x+2y=-5,用含y的式子表示x是 ,用含x的式子表示y是 .
作业:
如果一个长方形的周长为20cm,长为x cm,宽为y cm.
(1)请列出方程,并判断是否为二元一次方程.
(2)当x=6时,求y的值.
拓展训练:
THANK YOU!
感谢聆听
