1.7 整式的除法 第2课时 多项式除以单项式 精品课件(共19张PPT)
文档属性
| 名称 | 1.7 整式的除法 第2课时 多项式除以单项式 精品课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 774.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 10:59:06 | ||
图片预览



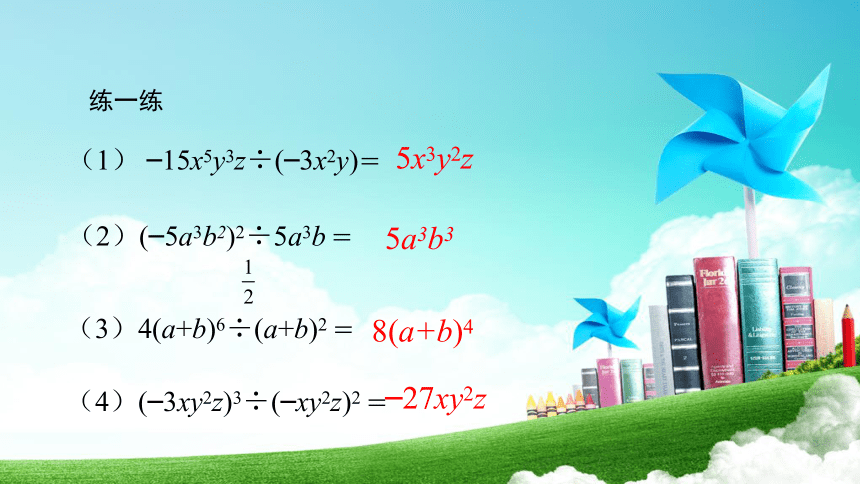
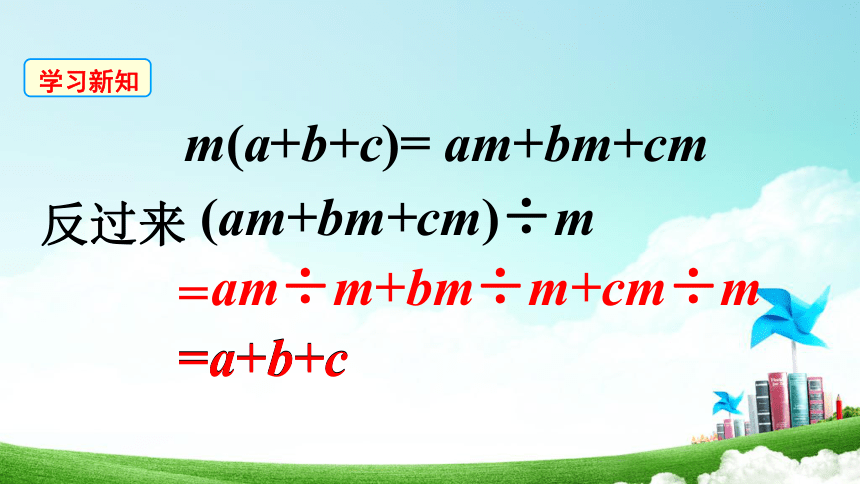


文档简介
(共19张PPT)
1.7 整式的除法
第一章 整式的乘除
第2课时 多项式除以单项式
学习目标
1.理解和掌握多项式除以单项式的运算法则;(重点)
2.会进行简单的多项式除以单项式的运算.(难点)
1.系数
2.同底数幂
3.只在被除式里的幂
相除;
相除;
不变.
知识回顾
单项式与单项式相除
(1) –15x5y3z÷(–3x2y)=
(2)(–5a3b2)2÷5a3b =
(3)4(a+b)6÷(a+b)2 =
(4)(–3xy2z)3÷(–xy2z)2 =
练一练
5x3y2z
5a3b3
8(a+b)4
–27xy2z
m(a+b+c)= am+bm+cm
=a+b+c
(am+bm+cm)÷m
am÷m+bm÷m+cm÷m
=a+b+c
=
反过来
学习新知
计算下列各题,并说说你的理由。
(1)(ac+bc)÷c=__________
(2)(x2y+3xy)÷x=_________
(3)(ab3-2ab)÷(ab)=_______
多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加。
a+b
xy+3y
b2-2
你找到了 多项式除以单项式的规律 吗?
把多项式除以单项式转化为单项式除以单项式.
法则
例1 计算:
(1)(6ab+8b)÷2b; (2)(27a3-15a2+6a)÷3a;
解:
(1)原式=6ab÷2b+8b÷2b
=3a+4;
典例精析
(2)原式=27a3÷3a-15a2÷3a+
6a÷3a
=9a2-5a+2;
(3)(9x2y-6xy2)÷3xy; (4)(3x2y-xy2+ xy)÷( xy).
解: (3)原式=9x2y÷3xy-6xy2÷3xy
=3x-2y;
(4)原式=-3x2y÷ xy+xy2÷ xy- xy÷ xy
=-6x+2y-1.
商的项数与多项式的项数相同
巩固练习1
例2 先化简,后求值:[2a(a2b-ab2)+ab(ab- a2)]÷a2b,
其中a=2022,b=2021.
解:[2a(a2b-ab2)+ab(ab-a2)]÷a2b
=(2a3b-2a2b2+a2b2-a3b)÷a2b
=(a3b-a2b2)÷a2b
=a-b
当a=2022,b=2021时,
原式=a-b=2022-2021=1.
1.判断下列计算是否正确,若不正确,指出错误的地方
(1)(4a2b-8ab)÷4ab=0.5a
(2)(5x3y-10x2y2-15xy3)÷(-5xy)=x2+2xy+3y2 ( )
(3)(2a2y-4ab2+6b3)÷ =-a2+2ab-3b2
当堂过关练
2. 4a3b2与一个多项式的积为20a5b2-16a3b4+68(a2b3)2,
则这个多项式为( )
A.5a2-4b2 B.5a2b-4ab2
C.5a2-4b2+17ab4 D.5a2-4b2+17ab3
C
3. 已知一多项式与单项式-6x5y4 的积为24x5y7-30x6y5,
则这个多项式是 .
-4y3+5xy
4.一个长方形的面积为a4-2a2b+a3,宽为a2,则长方形的长为________.
a2-2b+1
5.先化简,再求值:[(ab+3)(ab-3)-2(a2b2-3)]÷ab,
其中a=1,b=-2.
解:[(ab+3)(ab-3)-2(a2b2-3)]÷ab
=[(ab)2-32-2a2b2+9]÷ab
=(a2b2-9-2a2b2+9)÷ab
=(-a2b2)÷ab
=-ab.
当a=1,b=-2时,原式=-1×(-2)=2.
6.计算:
将(a+b)看作一个整体.
.
整体思想
小明在爬一小山时,第一阶段的平均速度为v,所用时间为 t1;第二阶段的平均速度为 v,所用时间为t2.下山时,小明的平均速度保持为4v.已知小明上山的路程和下山的路程是相同的,问小明下山用了多长时间?
拓展延伸:
( vt2+vt1)÷4v=
答:小明下山所用时间为
我学到了什么?
知识
思想 方法
数学中的转化思想
类比、归纳方法
多项式除以
单项式的法则
课堂小结
作业布置:习 题 1.14
1.必做题 第 1 题
2.挑战题 第 3题
1.7 整式的除法
第一章 整式的乘除
第2课时 多项式除以单项式
学习目标
1.理解和掌握多项式除以单项式的运算法则;(重点)
2.会进行简单的多项式除以单项式的运算.(难点)
1.系数
2.同底数幂
3.只在被除式里的幂
相除;
相除;
不变.
知识回顾
单项式与单项式相除
(1) –15x5y3z÷(–3x2y)=
(2)(–5a3b2)2÷5a3b =
(3)4(a+b)6÷(a+b)2 =
(4)(–3xy2z)3÷(–xy2z)2 =
练一练
5x3y2z
5a3b3
8(a+b)4
–27xy2z
m(a+b+c)= am+bm+cm
=a+b+c
(am+bm+cm)÷m
am÷m+bm÷m+cm÷m
=a+b+c
=
反过来
学习新知
计算下列各题,并说说你的理由。
(1)(ac+bc)÷c=__________
(2)(x2y+3xy)÷x=_________
(3)(ab3-2ab)÷(ab)=_______
多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加。
a+b
xy+3y
b2-2
你找到了 多项式除以单项式的规律 吗?
把多项式除以单项式转化为单项式除以单项式.
法则
例1 计算:
(1)(6ab+8b)÷2b; (2)(27a3-15a2+6a)÷3a;
解:
(1)原式=6ab÷2b+8b÷2b
=3a+4;
典例精析
(2)原式=27a3÷3a-15a2÷3a+
6a÷3a
=9a2-5a+2;
(3)(9x2y-6xy2)÷3xy; (4)(3x2y-xy2+ xy)÷( xy).
解: (3)原式=9x2y÷3xy-6xy2÷3xy
=3x-2y;
(4)原式=-3x2y÷ xy+xy2÷ xy- xy÷ xy
=-6x+2y-1.
商的项数与多项式的项数相同
巩固练习1
例2 先化简,后求值:[2a(a2b-ab2)+ab(ab- a2)]÷a2b,
其中a=2022,b=2021.
解:[2a(a2b-ab2)+ab(ab-a2)]÷a2b
=(2a3b-2a2b2+a2b2-a3b)÷a2b
=(a3b-a2b2)÷a2b
=a-b
当a=2022,b=2021时,
原式=a-b=2022-2021=1.
1.判断下列计算是否正确,若不正确,指出错误的地方
(1)(4a2b-8ab)÷4ab=0.5a
(2)(5x3y-10x2y2-15xy3)÷(-5xy)=x2+2xy+3y2 ( )
(3)(2a2y-4ab2+6b3)÷ =-a2+2ab-3b2
当堂过关练
2. 4a3b2与一个多项式的积为20a5b2-16a3b4+68(a2b3)2,
则这个多项式为( )
A.5a2-4b2 B.5a2b-4ab2
C.5a2-4b2+17ab4 D.5a2-4b2+17ab3
C
3. 已知一多项式与单项式-6x5y4 的积为24x5y7-30x6y5,
则这个多项式是 .
-4y3+5xy
4.一个长方形的面积为a4-2a2b+a3,宽为a2,则长方形的长为________.
a2-2b+1
5.先化简,再求值:[(ab+3)(ab-3)-2(a2b2-3)]÷ab,
其中a=1,b=-2.
解:[(ab+3)(ab-3)-2(a2b2-3)]÷ab
=[(ab)2-32-2a2b2+9]÷ab
=(a2b2-9-2a2b2+9)÷ab
=(-a2b2)÷ab
=-ab.
当a=1,b=-2时,原式=-1×(-2)=2.
6.计算:
将(a+b)看作一个整体.
.
整体思想
小明在爬一小山时,第一阶段的平均速度为v,所用时间为 t1;第二阶段的平均速度为 v,所用时间为t2.下山时,小明的平均速度保持为4v.已知小明上山的路程和下山的路程是相同的,问小明下山用了多长时间?
拓展延伸:
( vt2+vt1)÷4v=
答:小明下山所用时间为
我学到了什么?
知识
思想 方法
数学中的转化思想
类比、归纳方法
多项式除以
单项式的法则
课堂小结
作业布置:习 题 1.14
1.必做题 第 1 题
2.挑战题 第 3题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
