1.5 平方差公式 第2课时 平方差公式的应用 精品课件(共19张PPT)
文档属性
| 名称 | 1.5 平方差公式 第2课时 平方差公式的应用 精品课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 392.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 11:04:12 | ||
图片预览






文档简介
(共19张PPT)
第一章 整式的乘除
1.5平方差公式
第2课时 平方差公式的应用
七年级数学下(北师大版)
1.掌握平方差公式的结构特征,能运用公式进行简
便运算;(重点)
2.会用几何图形说明公式的意义,体会数形结合的
思想方法.(难点)
学习目标
知识回顾
1.什么是平方差公式?
(a+b)(a b)=a2 b2
3.利用平方差公式计算:
(1)(3x+4y)(3x–4y);
(2)(-a+2b)(a+2b).
9x2-12y2
4b2-a2
2、公式的结构特点:左边是两个二项式的乘积,即两数和与这两数差的积;右边是两数的平方差。
应用平方差公式的注意事项:
(1) ( x + 3) ( x – 3) = x2 - 32=x2 -9
(2) ( 2a + 3 ) ( 2a –3 ) = 4a2 –32
(3) ( x - 2y ) (-x- 2y ) = -x2 +4y2
(4) ( 2m + n ) ( 2m – n ) = 4m2 - n2
巩固基础1
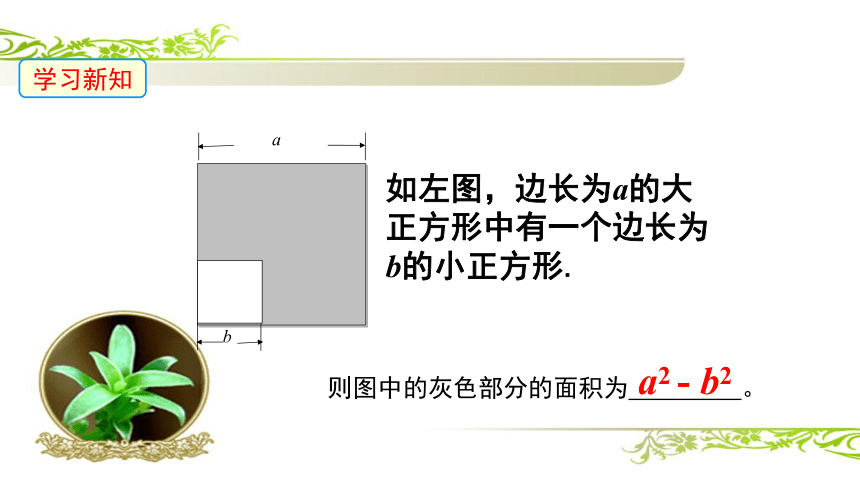
a
b
如左图,边长为a的大正方形中有一个边长为b的小正方形.
学习新知
则图中的灰色部分的面积为 。
a2 - b2
(1)小明将阴影部分拼成了一个长方形,如上图,这个长方形的长和宽分别是 它的面积表示为 。
a
b
a
b
用2种不同的方法表示图形的面积
a + b 、a –b
( a + b ) ( a – b )
a
b
a
b
(2)比较两个图形,你能验证平方差公式吗?
几何验证平方差公式
( a + b ) ( a - b ) = a2 - b2
运用平方差公式计算:
(1) ( x + 4 ) ( x –4 ) (x2 + 16 )
(2)
(3) a2 ( a + b ) ( a –b) +a2b2
(4) ( 2x – 3 ) ( 2x + 3 ) - 2x ( 2x – 1 )
巩固基础2
(1)计算下列各式,并观察他们的共同特点:
7×9=63 11×13=143 79×81=6399
8×8=64 12×12=144 80×80=6400
(2)你发现了什么规律?请用字母表示这一规律,并用所学知识验证发现的规律。
拓展延深
典例精析
例1 用平方差公式计算:
(1) 103×97; (2) 118×122.
解: 103×97
=(100+3)(100-3)
= 1002-32
=10000 – 9
=9991;
解: 118×122
=(120-2)(120+2)
= 1202-22
=14400-4
=14396.
注意:不能直接应用公式的,要经过变形才可以应用
例2 计算:
(1)a2(a+b)(a-b)+a2b2;
(2)(2x-5)(2x+5) –2x(2x-3) .
解:(1)原式=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4;
(2)原式=(2x)2-25-(4x2-6x)
=4x2-25-4x2+6x
=6x-25.
1.已知x=6302,y=629×631,则( )
A.x=y B.x>y
C.x2.197×203=( )×( )=( ).
3.(a+4)(a-4)-a(a-8)=0的解是______.
200-3
200+3
39991
a=2
B
当堂过关练
解:(1)原式=(60+2)(60-2)
=602-22
=3600-4=3596;
(3)原式=(16x2-9)-(6x2-5x-6)
=10x2-5x-3.
(1)62×58;
(3)(4x+3)(4x-3)-(3x+2)(2x-3).
(2)21.2×20.8;
4.利用平方差公式计算:
(2)原式=(21+0.2)×(21-0.2)
=212-0.22
=441-0.04=440.96;
(4) 20212 -2022×2020;
解:20212-2022×2020
=20212-(2021+1)(2021-1)
=20212-(20212-1)
=20212-20212+1
=1
(5) (x+2) (x-2) – (x-1) (x+5) .
解:(x+2)(x-2)- (x-1)(x+5)
= x2-22-(x2+4x-5)
= x2-4-x2-4x+5
= -4x + 1.
拓展延申
整体思想
课堂小结
1.本节课你学会了什么?
2.用到了哪些数学思想方法?
3.能解决什么样的问题?
平方差公式
验证
应用
利用几何图形的面积相等是验证平方差公式成立的核心思想
运用平方差公式简便计算问题的关键是确定a和b:
a=两数和的平均数
b=两数差的绝对值的平均数
课堂小结
作业布置:习 题 1.10
1.必做题 第 1 题
2.挑战题 第 2题
第一章 整式的乘除
1.5平方差公式
第2课时 平方差公式的应用
七年级数学下(北师大版)
1.掌握平方差公式的结构特征,能运用公式进行简
便运算;(重点)
2.会用几何图形说明公式的意义,体会数形结合的
思想方法.(难点)
学习目标
知识回顾
1.什么是平方差公式?
(a+b)(a b)=a2 b2
3.利用平方差公式计算:
(1)(3x+4y)(3x–4y);
(2)(-a+2b)(a+2b).
9x2-12y2
4b2-a2
2、公式的结构特点:左边是两个二项式的乘积,即两数和与这两数差的积;右边是两数的平方差。
应用平方差公式的注意事项:
(1) ( x + 3) ( x – 3) = x2 - 32=x2 -9
(2) ( 2a + 3 ) ( 2a –3 ) = 4a2 –32
(3) ( x - 2y ) (-x- 2y ) = -x2 +4y2
(4) ( 2m + n ) ( 2m – n ) = 4m2 - n2
巩固基础1
a
b
如左图,边长为a的大正方形中有一个边长为b的小正方形.
学习新知
则图中的灰色部分的面积为 。
a2 - b2
(1)小明将阴影部分拼成了一个长方形,如上图,这个长方形的长和宽分别是 它的面积表示为 。
a
b
a
b
用2种不同的方法表示图形的面积
a + b 、a –b
( a + b ) ( a – b )
a
b
a
b
(2)比较两个图形,你能验证平方差公式吗?
几何验证平方差公式
( a + b ) ( a - b ) = a2 - b2
运用平方差公式计算:
(1) ( x + 4 ) ( x –4 ) (x2 + 16 )
(2)
(3) a2 ( a + b ) ( a –b) +a2b2
(4) ( 2x – 3 ) ( 2x + 3 ) - 2x ( 2x – 1 )
巩固基础2
(1)计算下列各式,并观察他们的共同特点:
7×9=63 11×13=143 79×81=6399
8×8=64 12×12=144 80×80=6400
(2)你发现了什么规律?请用字母表示这一规律,并用所学知识验证发现的规律。
拓展延深
典例精析
例1 用平方差公式计算:
(1) 103×97; (2) 118×122.
解: 103×97
=(100+3)(100-3)
= 1002-32
=10000 – 9
=9991;
解: 118×122
=(120-2)(120+2)
= 1202-22
=14400-4
=14396.
注意:不能直接应用公式的,要经过变形才可以应用
例2 计算:
(1)a2(a+b)(a-b)+a2b2;
(2)(2x-5)(2x+5) –2x(2x-3) .
解:(1)原式=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4;
(2)原式=(2x)2-25-(4x2-6x)
=4x2-25-4x2+6x
=6x-25.
1.已知x=6302,y=629×631,则( )
A.x=y B.x>y
C.x
3.(a+4)(a-4)-a(a-8)=0的解是______.
200-3
200+3
39991
a=2
B
当堂过关练
解:(1)原式=(60+2)(60-2)
=602-22
=3600-4=3596;
(3)原式=(16x2-9)-(6x2-5x-6)
=10x2-5x-3.
(1)62×58;
(3)(4x+3)(4x-3)-(3x+2)(2x-3).
(2)21.2×20.8;
4.利用平方差公式计算:
(2)原式=(21+0.2)×(21-0.2)
=212-0.22
=441-0.04=440.96;
(4) 20212 -2022×2020;
解:20212-2022×2020
=20212-(2021+1)(2021-1)
=20212-(20212-1)
=20212-20212+1
=1
(5) (x+2) (x-2) – (x-1) (x+5) .
解:(x+2)(x-2)- (x-1)(x+5)
= x2-22-(x2+4x-5)
= x2-4-x2-4x+5
= -4x + 1.
拓展延申
整体思想
课堂小结
1.本节课你学会了什么?
2.用到了哪些数学思想方法?
3.能解决什么样的问题?
平方差公式
验证
应用
利用几何图形的面积相等是验证平方差公式成立的核心思想
运用平方差公式简便计算问题的关键是确定a和b:
a=两数和的平均数
b=两数差的绝对值的平均数
课堂小结
作业布置:习 题 1.10
1.必做题 第 1 题
2.挑战题 第 2题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
