1.6 完全平方式 第1课时 完全平方式的认识 精品课件(共23张PPT)
文档属性
| 名称 | 1.6 完全平方式 第1课时 完全平方式的认识 精品课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 555.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 11:08:16 | ||
图片预览








文档简介
(共23张PPT)
第一章 整式的乘除
1.6完全平方公
第1课时 完全平方公式的认识
七年级数学下(北师大版)
学习目标
1.理解并掌握完全平方公式的推导过程、结构特点;
(重点)
2.会运用公式进行简单的运算.(难点)
知识回顾
1、平方差公式 (a+b)(a b)=a2 - b2
抢答下列计算结果
(1)(6+5m)(6-5m)
(2)(a-3b)(a+3b)
(3)(-x+y)(-x-ny)
2、计算下列各式,并观察算式及其运算结果,你有什么发现?
(1)(x+3) 2 (2)(2+3m)2
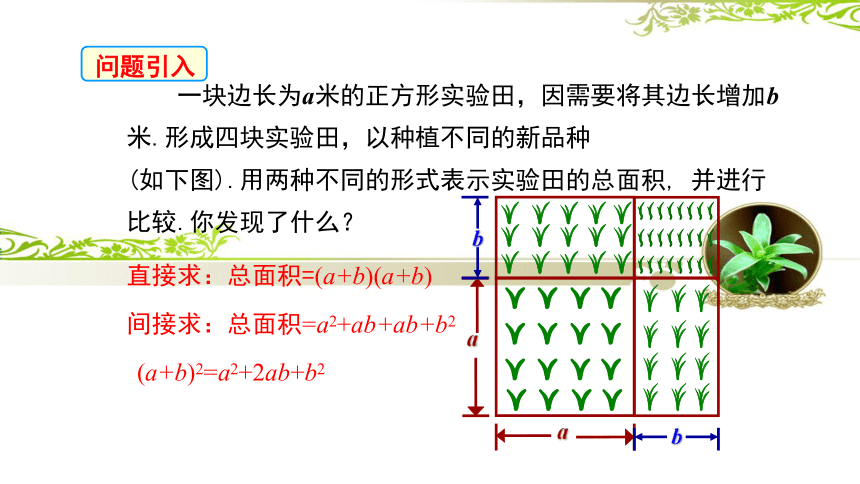
问题引入
一块边长为a米的正方形实验田,因需要将其边长增加b米.形成四块实验田,以种植不同的新品种
(如下图).用两种不同的形式表示实验田的总面积, 并进行
比较.你发现了什么?
a
a
b
b
直接求:总面积=(a+b)(a+b)
间接求:总面积=a2+ab+ab+b2
(a+b)2=a2+2ab+b2
猜一猜
(a+b) 2 =
a2+2ab+b2
你能用自己的语言叙述这一公式吗?
两数和的平方,等于这两数的平方和再加上这两数积的两倍.
简记为:
“首平方,尾平方,
2倍乘积在中央”
a
a
b
b
几何验证
(a+b) 2 =
a2+2ab+b2
根据刚才的发现计算下列多项式的积:
(1) (x+1)2=(x+1)(x+1)= .
x2+2x+1
(2) (p+2)2=(p+2)(p+2)= .
p2+4p+4
(3) (a-1)2=(a-1)(a-1)= .
a2-2a+1
(4) (p-2)2=(p-2)(p-2)= .
p2-4p+4
根据上面的规律,你能直接写出下面式子的答案吗?
(a-b)2= .
a2-2ab+b2
探究新知
归纳总结1
完全平方公式
(a+b)2= .
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫做完全平方公式.
简记为:
“首平方,尾平方,
2倍乘积在中央”
公式特点:
1.左边为二次三项式;
2.左边中的两项分别为两数的平方;
3.另一项是两数积的2倍,且与乘式中间的符号相同;
4.公式中的字母a,b可以表示数,单项式和多项式.
你能根据下图解释差的完全平方公式吗
b
a
b
a
试一试一想:
a2
ab b(a b)
=a2 2ab+b2 .
=
(a b)2
典例精析
例1 运用完全平方公式计算:
解: (3x-2)2=
=9x2
(1)(3x-2)2;
( a- b )2 =a2 - 2ab + b2
(3x)2
-2 (3x) 2
+22
-12x
+94;
确定a,b
(a + b)2= a2 + 2 ab + b2
( 5x )2
(2) ( 5x+ 4y )2;
=25x2+40xy+16y2.
+ ( 4y )2
+2 4x 5y
解:( 5x+4y )2 =
(a - b)2= a2 - 2 ab + b2
( mn )2
(3) ( mn-a )2.
=m2n2-2mna+a2.
+ a2
-2 mn a
解:( mn-a )2 =
(2) ( y+ )2.
(2)原式 =y2
+ y
+
针对练习1
例2 运用乘法公式计算:
(1) (x+2y-3)(x-2y+3) ;
解: 原式=[x+(2y-3)][x-(2y-3)]
= x2-(2y-3)2
= x2-(4y2-12y+9)
= x2-4y2+12y-9.
“符号相同的为一组,符号相反的为另一组”.
拓展提升
公式中的字母a,b可以表示数,单项式和多项式.
(2) (a+b-5)2.
解:原式= [(a+b)-5]2
= (a+b)2-10(a+b)+52
= a2+2ab+b2-10a-10b+25.
针对练习2
整体思想
例3 如果25a2+(m+1)ab+36b2是一个完全平
方式,求m的值.
解:∵25a2+(m+1)ab+36b2
=(±5a)2+(m+1)ab+(±6b)2,
∴(m+1)ab=±2·5a·6b,
∴m+1=±60,
∴m=59或-61.
公式逆用
如图的三角形可解释(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.
其中(a+b)0=1,
(a+b)1=a+b,
(a+b)2=a2+2ab+b2,
(a+b)3=a3+3a2b+3ab2+b3,
根据“杨辉三角”计算(a+b)4.
解:原式=a4+4a3b+6a2b2+4ab3+b4
课外阅读
1.在等号右边的括号内填上适当的项:
(1)x+y-z=x+( )
(2)x-y+z=x-( )
(3)x-y-z=x-( )
(4)x+y+z=x-( )
y-z
y-z
y+z
-y-z
能不能用去括号法则检查填写的是否正确
当堂过关练
1.添括号的法则:添括号时,如果括号前面是正号,括到括号里的各项的符号________;如果括号前面是负号,括到括号里的各项的符号________.
2.添括号的方法:
(1)遇________不变,遇________都变;
(2)添括号是否对,__________后来验证.
不变
添括号的法则
都变
“+”
“-”
去括号
知识补充
2.下面各式的计算是否正确?如果不正确,应当
怎样改正?
(1)(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (-x +y)2 =x2+2xy +y2
(4) (2x+y)2 =4x2 +2xy +y2
×
×
×
×
x2+2xy +y2
x2-2xy +y2
x2 -2xy +y2
4x2+4xy +y2
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;第一(二)数是乘积被平方时要注意添括号。
1、完全平方公式
2、运用完全平方公式计算时应注意什么?
(a+b)2 = a2+2ab+b2
(a-b)2 = a2 - 2ab+b2
课堂小结
作业布置:习 题 1.11
1.必做题 第 1 、2题
2.挑战题 第 3题
第一章 整式的乘除
1.6完全平方公
第1课时 完全平方公式的认识
七年级数学下(北师大版)
学习目标
1.理解并掌握完全平方公式的推导过程、结构特点;
(重点)
2.会运用公式进行简单的运算.(难点)
知识回顾
1、平方差公式 (a+b)(a b)=a2 - b2
抢答下列计算结果
(1)(6+5m)(6-5m)
(2)(a-3b)(a+3b)
(3)(-x+y)(-x-ny)
2、计算下列各式,并观察算式及其运算结果,你有什么发现?
(1)(x+3) 2 (2)(2+3m)2
问题引入
一块边长为a米的正方形实验田,因需要将其边长增加b米.形成四块实验田,以种植不同的新品种
(如下图).用两种不同的形式表示实验田的总面积, 并进行
比较.你发现了什么?
a
a
b
b
直接求:总面积=(a+b)(a+b)
间接求:总面积=a2+ab+ab+b2
(a+b)2=a2+2ab+b2
猜一猜
(a+b) 2 =
a2+2ab+b2
你能用自己的语言叙述这一公式吗?
两数和的平方,等于这两数的平方和再加上这两数积的两倍.
简记为:
“首平方,尾平方,
2倍乘积在中央”
a
a
b
b
几何验证
(a+b) 2 =
a2+2ab+b2
根据刚才的发现计算下列多项式的积:
(1) (x+1)2=(x+1)(x+1)= .
x2+2x+1
(2) (p+2)2=(p+2)(p+2)= .
p2+4p+4
(3) (a-1)2=(a-1)(a-1)= .
a2-2a+1
(4) (p-2)2=(p-2)(p-2)= .
p2-4p+4
根据上面的规律,你能直接写出下面式子的答案吗?
(a-b)2= .
a2-2ab+b2
探究新知
归纳总结1
完全平方公式
(a+b)2= .
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫做完全平方公式.
简记为:
“首平方,尾平方,
2倍乘积在中央”
公式特点:
1.左边为二次三项式;
2.左边中的两项分别为两数的平方;
3.另一项是两数积的2倍,且与乘式中间的符号相同;
4.公式中的字母a,b可以表示数,单项式和多项式.
你能根据下图解释差的完全平方公式吗
b
a
b
a
试一试一想:
a2
ab b(a b)
=a2 2ab+b2 .
=
(a b)2
典例精析
例1 运用完全平方公式计算:
解: (3x-2)2=
=9x2
(1)(3x-2)2;
( a- b )2 =a2 - 2ab + b2
(3x)2
-2 (3x) 2
+22
-12x
+94;
确定a,b
(a + b)2= a2 + 2 ab + b2
( 5x )2
(2) ( 5x+ 4y )2;
=25x2+40xy+16y2.
+ ( 4y )2
+2 4x 5y
解:( 5x+4y )2 =
(a - b)2= a2 - 2 ab + b2
( mn )2
(3) ( mn-a )2.
=m2n2-2mna+a2.
+ a2
-2 mn a
解:( mn-a )2 =
(2) ( y+ )2.
(2)原式 =y2
+ y
+
针对练习1
例2 运用乘法公式计算:
(1) (x+2y-3)(x-2y+3) ;
解: 原式=[x+(2y-3)][x-(2y-3)]
= x2-(2y-3)2
= x2-(4y2-12y+9)
= x2-4y2+12y-9.
“符号相同的为一组,符号相反的为另一组”.
拓展提升
公式中的字母a,b可以表示数,单项式和多项式.
(2) (a+b-5)2.
解:原式= [(a+b)-5]2
= (a+b)2-10(a+b)+52
= a2+2ab+b2-10a-10b+25.
针对练习2
整体思想
例3 如果25a2+(m+1)ab+36b2是一个完全平
方式,求m的值.
解:∵25a2+(m+1)ab+36b2
=(±5a)2+(m+1)ab+(±6b)2,
∴(m+1)ab=±2·5a·6b,
∴m+1=±60,
∴m=59或-61.
公式逆用
如图的三角形可解释(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.
其中(a+b)0=1,
(a+b)1=a+b,
(a+b)2=a2+2ab+b2,
(a+b)3=a3+3a2b+3ab2+b3,
根据“杨辉三角”计算(a+b)4.
解:原式=a4+4a3b+6a2b2+4ab3+b4
课外阅读
1.在等号右边的括号内填上适当的项:
(1)x+y-z=x+( )
(2)x-y+z=x-( )
(3)x-y-z=x-( )
(4)x+y+z=x-( )
y-z
y-z
y+z
-y-z
能不能用去括号法则检查填写的是否正确
当堂过关练
1.添括号的法则:添括号时,如果括号前面是正号,括到括号里的各项的符号________;如果括号前面是负号,括到括号里的各项的符号________.
2.添括号的方法:
(1)遇________不变,遇________都变;
(2)添括号是否对,__________后来验证.
不变
添括号的法则
都变
“+”
“-”
去括号
知识补充
2.下面各式的计算是否正确?如果不正确,应当
怎样改正?
(1)(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (-x +y)2 =x2+2xy +y2
(4) (2x+y)2 =4x2 +2xy +y2
×
×
×
×
x2+2xy +y2
x2-2xy +y2
x2 -2xy +y2
4x2+4xy +y2
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;第一(二)数是乘积被平方时要注意添括号。
1、完全平方公式
2、运用完全平方公式计算时应注意什么?
(a+b)2 = a2+2ab+b2
(a-b)2 = a2 - 2ab+b2
课堂小结
作业布置:习 题 1.11
1.必做题 第 1 、2题
2.挑战题 第 3题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
