5.2 平行线及其判定 同步练习(含解析)
文档属性
| 名称 | 5.2 平行线及其判定 同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版七年级下 5.2平行线及其判定同步练习
一.选择题
1.(2021秋 阳山县期末)如图,不能推出a∥b的条件是( )
A.∠4=∠2 B.∠3+∠4=180° C.∠1=∠3 D.∠2+∠3=180°
2.(2021春 饶平县校级期中)在同一平面内,不重合的两条直线的位置关系是( )
A.平行 B.相交 C.相交或垂直 D.相交或平行
3.(2021秋 文山市期末)下列图形中,由∠1=∠2能得到AB∥CD的是( )
A.B. C. D.
4.(2021秋 道里区期末)如图,下列条件①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC,∠3=∠4;④∠BAD+∠ADC=180°.其中能判定AB∥CD的有( )
A.1个 B.2个 C.3个 D.4个
5.(2021秋 凤翔县期末)下列说法正确的是( )
A.过直线上一点有且只有一条直线与已知直线平行
B.不相交的两条直线叫做平行线
C.直线外一点到该直线的所有线段中垂线最短
D.过直线外一点有且只有一条直线与已知直线平行
6.(2021秋 内江期末)在下面各图中,∠1=∠2,能判断AB∥CD的是( )
A.B.C.D.
7.(2021秋 南岗区校级期中)下列说法:
①和为180°且有一条公共边的两个角是邻补角;
②过一点有且只有一条直线与已知直线垂直;
③同位角相等;
④经过直线外一点,有且只有一条直线与这条直线平行;
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
8.(2021秋 余姚市期中)木条a、b、c如图用螺丝固定在木板α上且∠ABM=50°,∠DEM=70°,将木条a、木条b、木条c看作是在同一平面α内的三条直线AC、DF、MN,若使直线AC、直线DF达到平行的位置关系,则下列描述错误的是( )
A.木条b、c固定不动,木条a绕点B顺时针旋转20°
B.木条b、c固定不动,木条a绕点B逆时针旋转160°
C.木条a、c固定不动,木条b绕点E逆时针旋转20°
D.木条a、c固定不动,木条b绕点E顺时针旋转110°
9.(2021 曾都区一模)如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,下列能判定DE∥AC的条件是( )
A.∠1=∠3 B.∠3=∠C C.∠2=∠4 D.∠1+∠2=180°
二.填空题
10.(2021秋 杜尔伯特县期末)如图,不添加辅助线,请写出一个能判定AD∥BC的条件 .
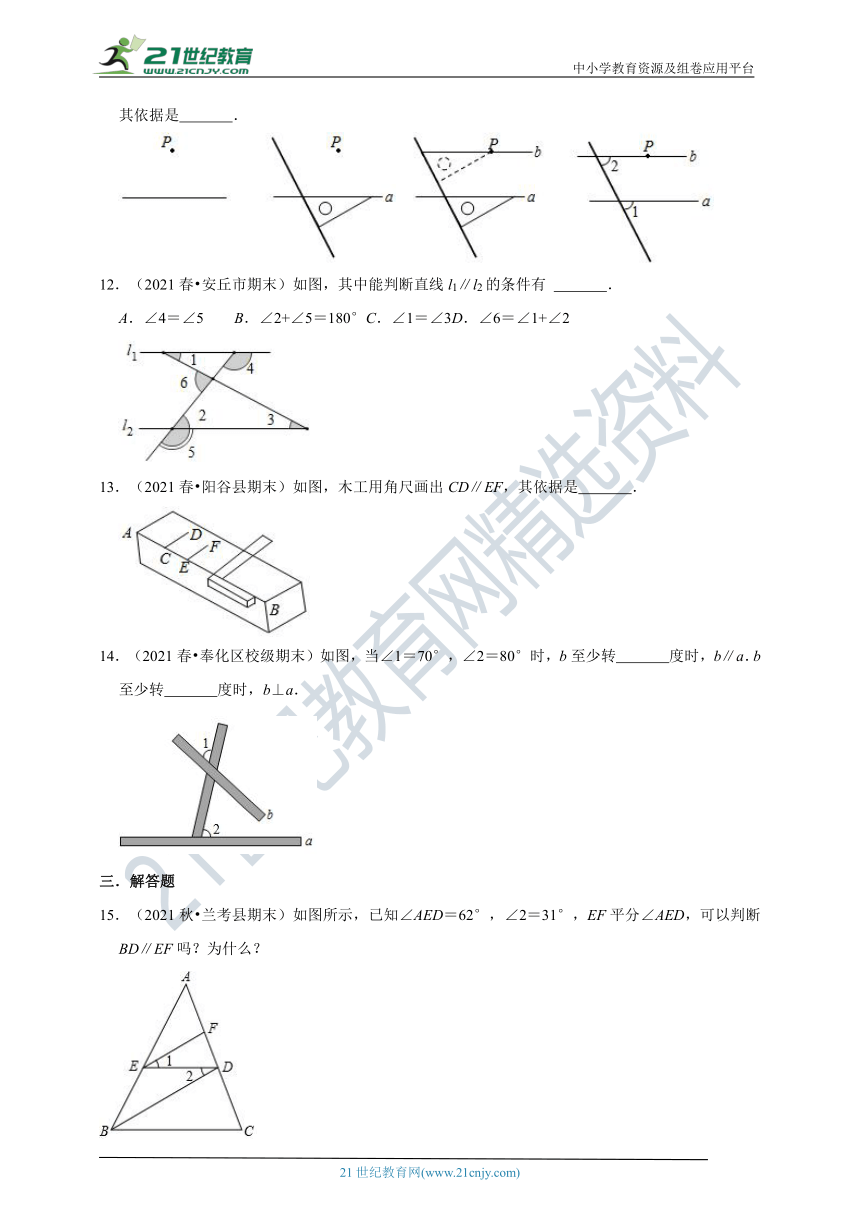
11.(2021春 鼓楼区校级期中)如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法,其依据是 .
12.(2021春 安丘市期末)如图,其中能判断直线l1∥l2的条件有 .
A.∠4=∠5 B.∠2+∠5=180°C.∠1=∠3D.∠6=∠1+∠2
13.(2021春 阳谷县期末)如图,木工用角尺画出CD∥EF,其依据是 .
14.(2021春 奉化区校级期末)如图,当∠1=70°,∠2=80°时,b至少转 度时,b∥a.b至少转 度时,b⊥a.
三.解答题
15.(2021秋 兰考县期末)如图所示,已知∠AED=62°,∠2=31°,EF平分∠AED,可以判断BD∥EF吗?为什么?
16.(2021春 利川市期末)在横线上填上适当的内容,完成下面的证明.
已知,直线a,b,c,d的位置如图所示,∠1+∠2=180°,∠3=∠4,求证:c∥d.
证明:如图,
∵∠2+∠3=180°( ),
∠1+∠2=180° ( ),
∴ = (同角的补角相等),
又∵∠3=∠4(已知),
∴∠1=∠4 ( ),
∴ ∥ ( ).
17.(2021秋 广南县期末)如图,点E为直线AB上一点,∠CAE=2∠B,BC平分∠ACD,求证:AB∥CD.
18.(2021春 普陀区校级月考)如图,点G在CD上,已知∠BAG+∠AGD=180°,EA平分∠BAG,FG平分∠AGC,请说明AE∥GF的理由.
解:因为∠BAG+∠AGD=180°( ),
∠AGC+∠AGD=180°( ),
所以∠BAG=∠AGC( ).
因为EA平分∠BAG,
所以∠1= ( ).
因为FG平分∠AGC,
所以∠2= ,
得∠1=∠2( ),
所以AE∥GF( ).
19.(2020秋 秦都区期末)如图,已知点E在直线DC上,射线EF平分∠AED,过E点作EB⊥EF,G为射线EC上一点,连接BG,且∠EBG+∠BEG=90°.
(1)求证:∠DEF=∠EBG;
(2)若∠EBG=∠A,求证:AB∥EF.
20.(2021秋 朝阳区校级期末)将一副三角板中的两块直角三角尺的直角顶点C按如图1方式叠放在一起,其中∠A=60°,∠D=30°,∠E=∠B=45°.
(1)若∠1=25°,则∠2的度数为 ;
(2)直接写出∠1与∠3的数量关系: ;
(3)直接写出∠2与∠ACB的数量关系: ;
(4)如图2,当∠ACE<180°且点E在直线AC的上方时,将三角尺ACD固定不动,改变三角尺BCE的位置,但始终保持两个三角尺的顶点C重合,这两块三角尺是否存在一组边互相平行?请直接写出∠ACE角度所有可能的值 .
答案与解析
一.选择题
1.(2021秋 阳山县期末)如图,不能推出a∥b的条件是( )
A.∠4=∠2 B.∠3+∠4=180° C.∠1=∠3 D.∠2+∠3=180°
【解析】解:∵∠4=∠2,
∴a∥b(内错角相等,两直线平行),故选项A不符合题意;
∠3+∠4=180°,不能得到a∥b,故选项B符合题意;
∵∠1=∠3,
∴a∥b(同位角相等,两直线平行),故选项C不符合题意;
∵∠2+∠3=180°,
∴a∥b(同旁内角互补,两直线平行),故选项D不符合题意;
故选:B.
2.(2021春 饶平县校级期中)在同一平面内,不重合的两条直线的位置关系是( )
A.平行 B.相交 C.相交或垂直 D.相交或平行
【解析】解:在同一平面内,不重合的两条直线的位置关系是相交或平行,相交包含垂直.
故选:D.
3.(2021秋 文山市期末)下列图形中,由∠1=∠2能得到AB∥CD的是( )
A.B. C. D.
【解析】解:A、∠1=∠2,AB∥CD,符合题意;
B、∠1+∠2=180°,AB∥CD,不符合题意;
C、∠1=∠2,得不出AB∥CD,不符合题意;
D、∠1=∠2,得不出AB∥CD,不符合题意;
故选:A.
4.(2021秋 道里区期末)如图,下列条件①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC,∠3=∠4;④∠BAD+∠ADC=180°.其中能判定AB∥CD的有( )
A.1个 B.2个 C.3个 D.4个
【解析】解:①由∠1=∠2可判定AD∥BC,不符合题意;
②由∠BAD=∠BCD不能判定AB∥BC,不符合题意;
③由∠ABC=∠ADC且∠3=∠4知∠ABD=∠CDB,可判定AB∥CD,符合题意;
④由∠BAD+∠ADC=180°可判定AB∥CD,符合题意;
故选:B.
5.(2021秋 凤翔县期末)下列说法正确的是( )
A.过直线上一点有且只有一条直线与已知直线平行
B.不相交的两条直线叫做平行线
C.直线外一点到该直线的所有线段中垂线最短
D.过直线外一点有且只有一条直线与已知直线平行
【解析】解:A、过直线外一点有且只有一条直线与已知直线平行,故原题说法错误;
B、同一平面内,不相交的两条直线叫做平行线,故原题说法错误;
C、直线外一点与该直线上所有点的连线中垂线最短,故原题说法错误;
D、过直线外一点有且只有一条直线与已知直线平行,故原题说法正确;
故选:D.
6.(2021秋 内江期末)在下面各图中,∠1=∠2,能判断AB∥CD的是( )
A.B.C.D.
【解析】解:第一个图中,∠1、∠2不是两条直线被第三条直线所截的内错角或同位角,不能判定AB∥CD;
第二个图中,∠1、∠2不是两条直线被第三条直线所截的同位角,不能判定AB∥CD;
第三个图中,∠1、∠2不是两条直线被第三条直线所截的同位角,不能判定AB∥CD;
第四个图中,∠1、∠2是两条直线被第三条直线所截的同位角,能判定AB∥CD;
故选:D.
7.(2021秋 南岗区校级期中)下列说法:
①和为180°且有一条公共边的两个角是邻补角;
②过一点有且只有一条直线与已知直线垂直;
③同位角相等;
④经过直线外一点,有且只有一条直线与这条直线平行;
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
【解析】解:①两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,叫做邻补角,原说法错误,不符合题意;
②在同一平面内,过一点有且只有一条直线与已知直线垂直;原说法错误,不符合题意;
③两直线平行,同位角相等;原说法错误,不符合题意;
④经过直线外一点,有且只有一条直线与这条直线平行;原说法正确,符合题意;
其中正确的有1个,
故选:B.
8.(2021秋 余姚市期中)木条a、b、c如图用螺丝固定在木板α上且∠ABM=50°,∠DEM=70°,将木条a、木条b、木条c看作是在同一平面α内的三条直线AC、DF、MN,若使直线AC、直线DF达到平行的位置关系,则下列描述错误的是( )
A.木条b、c固定不动,木条a绕点B顺时针旋转20°
B.木条b、c固定不动,木条a绕点B逆时针旋转160°
C.木条a、c固定不动,木条b绕点E逆时针旋转20°
D.木条a、c固定不动,木条b绕点E顺时针旋转110°
【解析】解:A.木条b、c固定不动,木条a绕点B顺时针旋转20°,
∴∠ABE=50°+20°=70°=∠DEM,
∴AC∥DF,
故A不符合题意;
B.木条b、c固定不动,木条a绕点B逆时针旋转160°,
∴∠CBE=50°+20°=70°=∠DEM,
∴AC∥DF,
故B不符合题意;
C.木条a、c固定不动,木条b绕点E逆时针旋转20°,
∴∠DEM=70°﹣20°=50°=∠ABE,
∴AC∥DF,
故C不符合题意;
D.木条a、c固定不动,木条b绕点E顺时针旋转110°,
∴木条b和木条c重合,AC与DF不平行,
故D符合题意.
故选:D.
9.(2021 曾都区一模)如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,下列能判定DE∥AC的条件是( )
A.∠1=∠3 B.∠3=∠C C.∠2=∠4 D.∠1+∠2=180°
【解析】解:A、当∠1=∠3时,EF∥BC,不符合题意;
B、当∠3=∠C时,DE∥AC,符合题意;
C、当∠2=∠4时,无法得到DE∥AC,不符合题意;
D、当∠1+∠2=180°时,EF∥BC,不符合题意.
故选:B.
二.填空题
10.(2021秋 杜尔伯特县期末)如图,不添加辅助线,请写出一个能判定AD∥BC的条件 ∠EAD=∠B或∠DAC=∠C或∠DAB+∠B=180° .
【解析】解:∵AD和BC被BE所截,
∴当∠EAD=∠B时,AD∥BC,
或当∠DAC=∠C时,AD∥BC,
或当∠DAB+∠B=180°时,AD∥BC,
故答案为:∠EAD=∠B或∠DAC=∠C或∠DAB+∠B=180°.
11.(2021春 鼓楼区校级期中)如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法,其依据是 同位角相等,两直线平行 .
【解析】解:过直线外一点画已知直线的平行线的方法叫“推平行线”法,其依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
12.(2021春 安丘市期末)如图,其中能判断直线l1∥l2的条件有 ACD .
A.∠4=∠5
B.∠2+∠5=180°
C.∠1=∠3
D.∠6=∠1+∠2
【解析】解:①∵∠4=∠5,∴l1∥l2,故本条件符合题意;
②由∠2+∠5=180°不能得到l1∥l2,故本条件不符合题意;
③∵∠1=∠3,∴l1∥l2,故本条件符合题意;
④∵∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴l1∥l2,故本条件符合题意.
故答案为:ACD.
13.(2021春 阳谷县期末)如图,木工用角尺画出CD∥EF,其依据是 同位角相等,两直线平行 .
【解析】解:木工用角尺画出CD∥EF,其依据是同位角相等,两直线平行,
故答案为:同位角相等,两直线平行.
14.(2021春 奉化区校级期末)如图,当∠1=70°,∠2=80°时,b至少转 30 度时,b∥a.b至少转 60 度时,b⊥a.
【解析】解:因为∠1=70°,
所以它的对顶角也等于70°.
当同旁内角互补的时候,b∥a,
因为∠2=80°,
所以180﹣80=100(度),
所以至少还需要转100﹣70=30(度);
将b顺时针旋转,与a垂直.
90﹣80=10(度),
所以至少还需要转70﹣10=60(度).
故答案为:30,60.
三.解答题
15.(2021秋 兰考县期末)如图所示,已知∠AED=62°,∠2=31°,EF平分∠AED,可以判断BD∥EF吗?为什么?
【解析】解:BD∥EF;理由如下:
∵∠AED=62°,EF平分∠AED,
∴∠1=∠AED=31°,
∵∠2=31°,
∴∠1=∠2,
∴BD∥EF.
16.(2021春 利川市期末)在横线上填上适当的内容,完成下面的证明.
已知,直线a,b,c,d的位置如图所示,∠1+∠2=180°,∠3=∠4,求证:c∥d.
证明:如图,
∵∠2+∠3=180°( 邻补角的定义 ),
∠1+∠2=180° ( 已知 ),
∴ ∠3 = ∠1 (同角的补角相等),
又∵∠3=∠4(已知),
∴∠1=∠4 ( 等量代换 ),
∴ c ∥ d ( 内错角相等,两直线平行 ).
【解析】证明:如图,
∵∠2+∠3=180°(邻补角的定义),
∠1+∠2=180° (已知),
∴∠3=∠1(同角的补角相等),
又∵∠3=∠4(已知),
∴∠1=∠4 (等量代换),
∴c∥d(内错角相等,两直线平行).
故答案为:邻补角的定义;已知;∠3;∠1;等量代换;c;d;内错角相等,两直线平行.
17.(2021秋 广南县期末)如图,点E为直线AB上一点,∠CAE=2∠B,BC平分∠ACD,求证:AB∥CD.
【解析】证明:由题意知∠CAE=∠ACB+∠B(三角形外角的性质),
∵∠CAE=2∠B(已知),
∴∠B=∠ACB(等量代换),
又∵BC平分∠ACD(已知),
∴∠ACB=∠DCB(角平分线的定义),
∴∠B=∠DCB(等量代换),
∴AB∥CD(内错角相等,两直线平行).
18.(2021春 普陀区校级月考)如图,点G在CD上,已知∠BAG+∠AGD=180°,EA平分∠BAG,FG平分∠AGC,请说明AE∥GF的理由.
解:因为∠BAG+∠AGD=180°( 已知 ),
∠AGC+∠AGD=180°( 邻补角的定义 ),
所以∠BAG=∠AGC( 同角的补角相等 ).
因为EA平分∠BAG,
所以∠1= ∠BAG ( 角平分线的定义 ).
因为FG平分∠AGC,
所以∠2= ∠AGC ,
得∠1=∠2( 等量代换 ),
所以AE∥GF( 内错角相等,两直线平行 ).
【解析】解:因为∠BAG+∠AGD=180°(已知),
∠AGC+∠AGD=180°(邻补角的定义),
所以∠BAG=∠AGC(同角的补角相等),
因为EA平分∠BAG,
所以∠1=∠BAG(角平分线的定义),
因为FG平分∠AGC,
所以∠2=∠AGC,
得∠1=∠2(等量代换),
所以AE∥GF(内错角相等,两直线平行).
故答案为:已知;邻补角的定义;同角的补角相等;∠BAG;角平分线的定义;∠AGC;等量代换;内错角相等,两直线平行.
19.(2020秋 秦都区期末)如图,已知点E在直线DC上,射线EF平分∠AED,过E点作EB⊥EF,G为射线EC上一点,连接BG,且∠EBG+∠BEG=90°.
(1)求证:∠DEF=∠EBG;
(2)若∠EBG=∠A,求证:AB∥EF.
【解析】证明:(1)∵EB⊥EF,
∴∠FEB=90°,
∴∠DEF+∠BEG=180°﹣90°=90°.
又∵∠EBG+∠BEG=90°,
∴∠DEF=∠EBG;
(2)∵∠EBG=∠A,∠DEF=∠EBG,
∴∠A=∠DEF.
∵EF平分∠AED,
∴∠AEF=∠DEF,
∴∠A=∠AEF,
∴AB//EF.
20.(2021秋 朝阳区校级期末)将一副三角板中的两块直角三角尺的直角顶点C按如图1方式叠放在一起,其中∠A=60°,∠D=30°,∠E=∠B=45°.
(1)若∠1=25°,则∠2的度数为 65° ;
(2)直接写出∠1与∠3的数量关系: ∠1=∠3 ;
(3)直接写出∠2与∠ACB的数量关系: ∠2+∠ACB=180° ;
(4)如图2,当∠ACE<180°且点E在直线AC的上方时,将三角尺ACD固定不动,改变三角尺BCE的位置,但始终保持两个三角尺的顶点C重合,这两块三角尺是否存在一组边互相平行?请直接写出∠ACE角度所有可能的值 30°或45°或120°或135°或165° .
【解析】解:(1)∵∠1=25°,∠ACD=90°,
∴∠2=∠ACD﹣∠1=65°,
故答案为:65°;
(2)∵∠1+∠2=∠ACD=90°,∠2+∠3=∠BCE=90°,
∴∠1+∠2=∠2+∠3,
∴∠1=∠3,
故答案为:∠1=∠3;
(3)∵∠ACD=∠BCE=90°,
∴∠ACB+∠2
=∠1+∠2+∠3+∠2
=∠ACD+∠BCE
=180°,
即∠2+∠ACB=180°,
故答案为:∠2+∠ACB=180°;
(4)存在,
①当BC∥AD时,
∵BC∥AD,
∴∠BCD=∠D=30°,
∴∠ACB=90°+30°=120°,
∴∠ACE=∠ACB﹣∠BCE=120°﹣90°=30°;
②当BE∥AC时,如图,
∵BE∥AC,
∴∠ACE=∠E=45°;
③当AD∥CE时,如图,
∵AD∥CE,
∴∠DCE=∠D=30°,
∴∠ACE=90°+30°=120°;
④当BE∥CD时,如图,
∵BE∥CD,
∴∠DCE=∠E=45°,
∴∠ACE=∠ACD+∠DCE=135°;
⑤当BE∥AD时,如图,
过点C作CF∥AD,
∵BE∥AD,CF∥AD,
∴BE∥AD∥CF,
∴∠ECF=∠E=45°,∠DCF=∠D=30°,
∴∠DCE=30°+45°=75°,
∴∠ACE=90°+75°=165°.
综上所述:当∠ACE=30°或45°或120°或135°或165°时,有一组边互相平行.
故答案为:30°或45°或120°或135°或165°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版七年级下 5.2平行线及其判定同步练习
一.选择题
1.(2021秋 阳山县期末)如图,不能推出a∥b的条件是( )
A.∠4=∠2 B.∠3+∠4=180° C.∠1=∠3 D.∠2+∠3=180°
2.(2021春 饶平县校级期中)在同一平面内,不重合的两条直线的位置关系是( )
A.平行 B.相交 C.相交或垂直 D.相交或平行
3.(2021秋 文山市期末)下列图形中,由∠1=∠2能得到AB∥CD的是( )
A.B. C. D.
4.(2021秋 道里区期末)如图,下列条件①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC,∠3=∠4;④∠BAD+∠ADC=180°.其中能判定AB∥CD的有( )
A.1个 B.2个 C.3个 D.4个
5.(2021秋 凤翔县期末)下列说法正确的是( )
A.过直线上一点有且只有一条直线与已知直线平行
B.不相交的两条直线叫做平行线
C.直线外一点到该直线的所有线段中垂线最短
D.过直线外一点有且只有一条直线与已知直线平行
6.(2021秋 内江期末)在下面各图中,∠1=∠2,能判断AB∥CD的是( )
A.B.C.D.
7.(2021秋 南岗区校级期中)下列说法:
①和为180°且有一条公共边的两个角是邻补角;
②过一点有且只有一条直线与已知直线垂直;
③同位角相等;
④经过直线外一点,有且只有一条直线与这条直线平行;
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
8.(2021秋 余姚市期中)木条a、b、c如图用螺丝固定在木板α上且∠ABM=50°,∠DEM=70°,将木条a、木条b、木条c看作是在同一平面α内的三条直线AC、DF、MN,若使直线AC、直线DF达到平行的位置关系,则下列描述错误的是( )
A.木条b、c固定不动,木条a绕点B顺时针旋转20°
B.木条b、c固定不动,木条a绕点B逆时针旋转160°
C.木条a、c固定不动,木条b绕点E逆时针旋转20°
D.木条a、c固定不动,木条b绕点E顺时针旋转110°
9.(2021 曾都区一模)如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,下列能判定DE∥AC的条件是( )
A.∠1=∠3 B.∠3=∠C C.∠2=∠4 D.∠1+∠2=180°
二.填空题
10.(2021秋 杜尔伯特县期末)如图,不添加辅助线,请写出一个能判定AD∥BC的条件 .
11.(2021春 鼓楼区校级期中)如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法,其依据是 .
12.(2021春 安丘市期末)如图,其中能判断直线l1∥l2的条件有 .
A.∠4=∠5 B.∠2+∠5=180°C.∠1=∠3D.∠6=∠1+∠2
13.(2021春 阳谷县期末)如图,木工用角尺画出CD∥EF,其依据是 .
14.(2021春 奉化区校级期末)如图,当∠1=70°,∠2=80°时,b至少转 度时,b∥a.b至少转 度时,b⊥a.
三.解答题
15.(2021秋 兰考县期末)如图所示,已知∠AED=62°,∠2=31°,EF平分∠AED,可以判断BD∥EF吗?为什么?
16.(2021春 利川市期末)在横线上填上适当的内容,完成下面的证明.
已知,直线a,b,c,d的位置如图所示,∠1+∠2=180°,∠3=∠4,求证:c∥d.
证明:如图,
∵∠2+∠3=180°( ),
∠1+∠2=180° ( ),
∴ = (同角的补角相等),
又∵∠3=∠4(已知),
∴∠1=∠4 ( ),
∴ ∥ ( ).
17.(2021秋 广南县期末)如图,点E为直线AB上一点,∠CAE=2∠B,BC平分∠ACD,求证:AB∥CD.
18.(2021春 普陀区校级月考)如图,点G在CD上,已知∠BAG+∠AGD=180°,EA平分∠BAG,FG平分∠AGC,请说明AE∥GF的理由.
解:因为∠BAG+∠AGD=180°( ),
∠AGC+∠AGD=180°( ),
所以∠BAG=∠AGC( ).
因为EA平分∠BAG,
所以∠1= ( ).
因为FG平分∠AGC,
所以∠2= ,
得∠1=∠2( ),
所以AE∥GF( ).
19.(2020秋 秦都区期末)如图,已知点E在直线DC上,射线EF平分∠AED,过E点作EB⊥EF,G为射线EC上一点,连接BG,且∠EBG+∠BEG=90°.
(1)求证:∠DEF=∠EBG;
(2)若∠EBG=∠A,求证:AB∥EF.
20.(2021秋 朝阳区校级期末)将一副三角板中的两块直角三角尺的直角顶点C按如图1方式叠放在一起,其中∠A=60°,∠D=30°,∠E=∠B=45°.
(1)若∠1=25°,则∠2的度数为 ;
(2)直接写出∠1与∠3的数量关系: ;
(3)直接写出∠2与∠ACB的数量关系: ;
(4)如图2,当∠ACE<180°且点E在直线AC的上方时,将三角尺ACD固定不动,改变三角尺BCE的位置,但始终保持两个三角尺的顶点C重合,这两块三角尺是否存在一组边互相平行?请直接写出∠ACE角度所有可能的值 .
答案与解析
一.选择题
1.(2021秋 阳山县期末)如图,不能推出a∥b的条件是( )
A.∠4=∠2 B.∠3+∠4=180° C.∠1=∠3 D.∠2+∠3=180°
【解析】解:∵∠4=∠2,
∴a∥b(内错角相等,两直线平行),故选项A不符合题意;
∠3+∠4=180°,不能得到a∥b,故选项B符合题意;
∵∠1=∠3,
∴a∥b(同位角相等,两直线平行),故选项C不符合题意;
∵∠2+∠3=180°,
∴a∥b(同旁内角互补,两直线平行),故选项D不符合题意;
故选:B.
2.(2021春 饶平县校级期中)在同一平面内,不重合的两条直线的位置关系是( )
A.平行 B.相交 C.相交或垂直 D.相交或平行
【解析】解:在同一平面内,不重合的两条直线的位置关系是相交或平行,相交包含垂直.
故选:D.
3.(2021秋 文山市期末)下列图形中,由∠1=∠2能得到AB∥CD的是( )
A.B. C. D.
【解析】解:A、∠1=∠2,AB∥CD,符合题意;
B、∠1+∠2=180°,AB∥CD,不符合题意;
C、∠1=∠2,得不出AB∥CD,不符合题意;
D、∠1=∠2,得不出AB∥CD,不符合题意;
故选:A.
4.(2021秋 道里区期末)如图,下列条件①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC,∠3=∠4;④∠BAD+∠ADC=180°.其中能判定AB∥CD的有( )
A.1个 B.2个 C.3个 D.4个
【解析】解:①由∠1=∠2可判定AD∥BC,不符合题意;
②由∠BAD=∠BCD不能判定AB∥BC,不符合题意;
③由∠ABC=∠ADC且∠3=∠4知∠ABD=∠CDB,可判定AB∥CD,符合题意;
④由∠BAD+∠ADC=180°可判定AB∥CD,符合题意;
故选:B.
5.(2021秋 凤翔县期末)下列说法正确的是( )
A.过直线上一点有且只有一条直线与已知直线平行
B.不相交的两条直线叫做平行线
C.直线外一点到该直线的所有线段中垂线最短
D.过直线外一点有且只有一条直线与已知直线平行
【解析】解:A、过直线外一点有且只有一条直线与已知直线平行,故原题说法错误;
B、同一平面内,不相交的两条直线叫做平行线,故原题说法错误;
C、直线外一点与该直线上所有点的连线中垂线最短,故原题说法错误;
D、过直线外一点有且只有一条直线与已知直线平行,故原题说法正确;
故选:D.
6.(2021秋 内江期末)在下面各图中,∠1=∠2,能判断AB∥CD的是( )
A.B.C.D.
【解析】解:第一个图中,∠1、∠2不是两条直线被第三条直线所截的内错角或同位角,不能判定AB∥CD;
第二个图中,∠1、∠2不是两条直线被第三条直线所截的同位角,不能判定AB∥CD;
第三个图中,∠1、∠2不是两条直线被第三条直线所截的同位角,不能判定AB∥CD;
第四个图中,∠1、∠2是两条直线被第三条直线所截的同位角,能判定AB∥CD;
故选:D.
7.(2021秋 南岗区校级期中)下列说法:
①和为180°且有一条公共边的两个角是邻补角;
②过一点有且只有一条直线与已知直线垂直;
③同位角相等;
④经过直线外一点,有且只有一条直线与这条直线平行;
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
【解析】解:①两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,叫做邻补角,原说法错误,不符合题意;
②在同一平面内,过一点有且只有一条直线与已知直线垂直;原说法错误,不符合题意;
③两直线平行,同位角相等;原说法错误,不符合题意;
④经过直线外一点,有且只有一条直线与这条直线平行;原说法正确,符合题意;
其中正确的有1个,
故选:B.
8.(2021秋 余姚市期中)木条a、b、c如图用螺丝固定在木板α上且∠ABM=50°,∠DEM=70°,将木条a、木条b、木条c看作是在同一平面α内的三条直线AC、DF、MN,若使直线AC、直线DF达到平行的位置关系,则下列描述错误的是( )
A.木条b、c固定不动,木条a绕点B顺时针旋转20°
B.木条b、c固定不动,木条a绕点B逆时针旋转160°
C.木条a、c固定不动,木条b绕点E逆时针旋转20°
D.木条a、c固定不动,木条b绕点E顺时针旋转110°
【解析】解:A.木条b、c固定不动,木条a绕点B顺时针旋转20°,
∴∠ABE=50°+20°=70°=∠DEM,
∴AC∥DF,
故A不符合题意;
B.木条b、c固定不动,木条a绕点B逆时针旋转160°,
∴∠CBE=50°+20°=70°=∠DEM,
∴AC∥DF,
故B不符合题意;
C.木条a、c固定不动,木条b绕点E逆时针旋转20°,
∴∠DEM=70°﹣20°=50°=∠ABE,
∴AC∥DF,
故C不符合题意;
D.木条a、c固定不动,木条b绕点E顺时针旋转110°,
∴木条b和木条c重合,AC与DF不平行,
故D符合题意.
故选:D.
9.(2021 曾都区一模)如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,下列能判定DE∥AC的条件是( )
A.∠1=∠3 B.∠3=∠C C.∠2=∠4 D.∠1+∠2=180°
【解析】解:A、当∠1=∠3时,EF∥BC,不符合题意;
B、当∠3=∠C时,DE∥AC,符合题意;
C、当∠2=∠4时,无法得到DE∥AC,不符合题意;
D、当∠1+∠2=180°时,EF∥BC,不符合题意.
故选:B.
二.填空题
10.(2021秋 杜尔伯特县期末)如图,不添加辅助线,请写出一个能判定AD∥BC的条件 ∠EAD=∠B或∠DAC=∠C或∠DAB+∠B=180° .
【解析】解:∵AD和BC被BE所截,
∴当∠EAD=∠B时,AD∥BC,
或当∠DAC=∠C时,AD∥BC,
或当∠DAB+∠B=180°时,AD∥BC,
故答案为:∠EAD=∠B或∠DAC=∠C或∠DAB+∠B=180°.
11.(2021春 鼓楼区校级期中)如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法,其依据是 同位角相等,两直线平行 .
【解析】解:过直线外一点画已知直线的平行线的方法叫“推平行线”法,其依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
12.(2021春 安丘市期末)如图,其中能判断直线l1∥l2的条件有 ACD .
A.∠4=∠5
B.∠2+∠5=180°
C.∠1=∠3
D.∠6=∠1+∠2
【解析】解:①∵∠4=∠5,∴l1∥l2,故本条件符合题意;
②由∠2+∠5=180°不能得到l1∥l2,故本条件不符合题意;
③∵∠1=∠3,∴l1∥l2,故本条件符合题意;
④∵∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴l1∥l2,故本条件符合题意.
故答案为:ACD.
13.(2021春 阳谷县期末)如图,木工用角尺画出CD∥EF,其依据是 同位角相等,两直线平行 .
【解析】解:木工用角尺画出CD∥EF,其依据是同位角相等,两直线平行,
故答案为:同位角相等,两直线平行.
14.(2021春 奉化区校级期末)如图,当∠1=70°,∠2=80°时,b至少转 30 度时,b∥a.b至少转 60 度时,b⊥a.
【解析】解:因为∠1=70°,
所以它的对顶角也等于70°.
当同旁内角互补的时候,b∥a,
因为∠2=80°,
所以180﹣80=100(度),
所以至少还需要转100﹣70=30(度);
将b顺时针旋转,与a垂直.
90﹣80=10(度),
所以至少还需要转70﹣10=60(度).
故答案为:30,60.
三.解答题
15.(2021秋 兰考县期末)如图所示,已知∠AED=62°,∠2=31°,EF平分∠AED,可以判断BD∥EF吗?为什么?
【解析】解:BD∥EF;理由如下:
∵∠AED=62°,EF平分∠AED,
∴∠1=∠AED=31°,
∵∠2=31°,
∴∠1=∠2,
∴BD∥EF.
16.(2021春 利川市期末)在横线上填上适当的内容,完成下面的证明.
已知,直线a,b,c,d的位置如图所示,∠1+∠2=180°,∠3=∠4,求证:c∥d.
证明:如图,
∵∠2+∠3=180°( 邻补角的定义 ),
∠1+∠2=180° ( 已知 ),
∴ ∠3 = ∠1 (同角的补角相等),
又∵∠3=∠4(已知),
∴∠1=∠4 ( 等量代换 ),
∴ c ∥ d ( 内错角相等,两直线平行 ).
【解析】证明:如图,
∵∠2+∠3=180°(邻补角的定义),
∠1+∠2=180° (已知),
∴∠3=∠1(同角的补角相等),
又∵∠3=∠4(已知),
∴∠1=∠4 (等量代换),
∴c∥d(内错角相等,两直线平行).
故答案为:邻补角的定义;已知;∠3;∠1;等量代换;c;d;内错角相等,两直线平行.
17.(2021秋 广南县期末)如图,点E为直线AB上一点,∠CAE=2∠B,BC平分∠ACD,求证:AB∥CD.
【解析】证明:由题意知∠CAE=∠ACB+∠B(三角形外角的性质),
∵∠CAE=2∠B(已知),
∴∠B=∠ACB(等量代换),
又∵BC平分∠ACD(已知),
∴∠ACB=∠DCB(角平分线的定义),
∴∠B=∠DCB(等量代换),
∴AB∥CD(内错角相等,两直线平行).
18.(2021春 普陀区校级月考)如图,点G在CD上,已知∠BAG+∠AGD=180°,EA平分∠BAG,FG平分∠AGC,请说明AE∥GF的理由.
解:因为∠BAG+∠AGD=180°( 已知 ),
∠AGC+∠AGD=180°( 邻补角的定义 ),
所以∠BAG=∠AGC( 同角的补角相等 ).
因为EA平分∠BAG,
所以∠1= ∠BAG ( 角平分线的定义 ).
因为FG平分∠AGC,
所以∠2= ∠AGC ,
得∠1=∠2( 等量代换 ),
所以AE∥GF( 内错角相等,两直线平行 ).
【解析】解:因为∠BAG+∠AGD=180°(已知),
∠AGC+∠AGD=180°(邻补角的定义),
所以∠BAG=∠AGC(同角的补角相等),
因为EA平分∠BAG,
所以∠1=∠BAG(角平分线的定义),
因为FG平分∠AGC,
所以∠2=∠AGC,
得∠1=∠2(等量代换),
所以AE∥GF(内错角相等,两直线平行).
故答案为:已知;邻补角的定义;同角的补角相等;∠BAG;角平分线的定义;∠AGC;等量代换;内错角相等,两直线平行.
19.(2020秋 秦都区期末)如图,已知点E在直线DC上,射线EF平分∠AED,过E点作EB⊥EF,G为射线EC上一点,连接BG,且∠EBG+∠BEG=90°.
(1)求证:∠DEF=∠EBG;
(2)若∠EBG=∠A,求证:AB∥EF.
【解析】证明:(1)∵EB⊥EF,
∴∠FEB=90°,
∴∠DEF+∠BEG=180°﹣90°=90°.
又∵∠EBG+∠BEG=90°,
∴∠DEF=∠EBG;
(2)∵∠EBG=∠A,∠DEF=∠EBG,
∴∠A=∠DEF.
∵EF平分∠AED,
∴∠AEF=∠DEF,
∴∠A=∠AEF,
∴AB//EF.
20.(2021秋 朝阳区校级期末)将一副三角板中的两块直角三角尺的直角顶点C按如图1方式叠放在一起,其中∠A=60°,∠D=30°,∠E=∠B=45°.
(1)若∠1=25°,则∠2的度数为 65° ;
(2)直接写出∠1与∠3的数量关系: ∠1=∠3 ;
(3)直接写出∠2与∠ACB的数量关系: ∠2+∠ACB=180° ;
(4)如图2,当∠ACE<180°且点E在直线AC的上方时,将三角尺ACD固定不动,改变三角尺BCE的位置,但始终保持两个三角尺的顶点C重合,这两块三角尺是否存在一组边互相平行?请直接写出∠ACE角度所有可能的值 30°或45°或120°或135°或165° .
【解析】解:(1)∵∠1=25°,∠ACD=90°,
∴∠2=∠ACD﹣∠1=65°,
故答案为:65°;
(2)∵∠1+∠2=∠ACD=90°,∠2+∠3=∠BCE=90°,
∴∠1+∠2=∠2+∠3,
∴∠1=∠3,
故答案为:∠1=∠3;
(3)∵∠ACD=∠BCE=90°,
∴∠ACB+∠2
=∠1+∠2+∠3+∠2
=∠ACD+∠BCE
=180°,
即∠2+∠ACB=180°,
故答案为:∠2+∠ACB=180°;
(4)存在,
①当BC∥AD时,
∵BC∥AD,
∴∠BCD=∠D=30°,
∴∠ACB=90°+30°=120°,
∴∠ACE=∠ACB﹣∠BCE=120°﹣90°=30°;
②当BE∥AC时,如图,
∵BE∥AC,
∴∠ACE=∠E=45°;
③当AD∥CE时,如图,
∵AD∥CE,
∴∠DCE=∠D=30°,
∴∠ACE=90°+30°=120°;
④当BE∥CD时,如图,
∵BE∥CD,
∴∠DCE=∠E=45°,
∴∠ACE=∠ACD+∠DCE=135°;
⑤当BE∥AD时,如图,
过点C作CF∥AD,
∵BE∥AD,CF∥AD,
∴BE∥AD∥CF,
∴∠ECF=∠E=45°,∠DCF=∠D=30°,
∴∠DCE=30°+45°=75°,
∴∠ACE=90°+75°=165°.
综上所述:当∠ACE=30°或45°或120°或135°或165°时,有一组边互相平行.
故答案为:30°或45°或120°或135°或165°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
