人教版七年级下册8.2.1消元——解二元一次方程组 课件(共17张)
文档属性
| 名称 | 人教版七年级下册8.2.1消元——解二元一次方程组 课件(共17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1018.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 09:15:09 | ||
图片预览






文档简介
(共17张PPT)
8.2.1消元——解二元一次方程组
问题1:把下列方程写成用含x的式子表示y的形式和用含y的式子表示x的形式
“雪糕”问题
超市有2元和3元两种雪糕,陈老师准备买雪糕来奖励给班上上课积极的同学,由于单买一种雪糕,数量不够,所以两种同时购买,一共花费了52元,其中2元的雪糕数量比3元的雪糕数量多1,请问陈老师购买的两种雪糕各有多少支?
同学们,你们能用一元一次方程解决这个“雪糕”问题吗?
解:设2元的雪糕数量为x支,则3元的雪糕数量为(x-1)支。
由题意可得方程
2x + 3(x-1) = 52
解得 x = 11
则 x-1 = 11-1 = 10
答:陈老师购买的2元的雪糕有11支,3元的雪糕有10支。
你能列二元一次方程组解决这个问题吗?
解:2元的雪糕数量为x支,3元的雪糕数量为y支
由题意可得方程组
“雪糕”问题
超市有2元和3元两种雪糕,陈老师准备买雪糕来奖励给班上上课积极的同学,由于单买一种雪糕,数量不够,所以两种同时购买,一共花费了52元,其中2元的雪糕数量比3元的雪糕数量多1,请问陈老师购买的两种雪糕各有多少支?
如何解这个二元一次方程组解决呢 ?
分析:
2元雪糕总费用+3元雪糕总费用=52
2元雪糕数量=3元雪糕数量+1
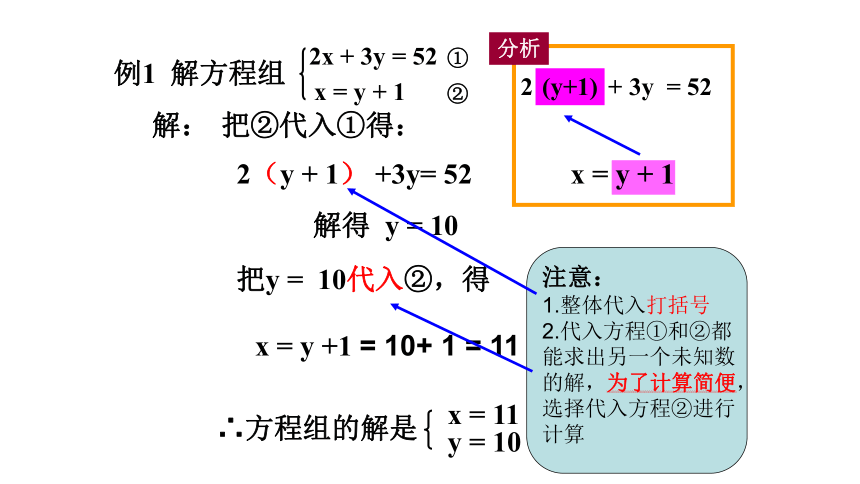
例1 解方程组
2x + 3y = 52
x = y + 1
①
②
分析:该方程组中,方程②是用含 的式子表示 。
能。方程②是用含y的式子表示x,可将方程①中的x看成y+1,此时方程①就只剩下y一个未知数,即为一元一次方程。
y
x
小组讨论:
1.方程①中的x能否也用方程②中含y的式子来表示,为什么?
2.能否将该方程组变为一元一次方程进行求解,为什么?
能。因为方程组的解是两个方程的公共解,同一个未知数的值相等。
分析
解:
例1 解方程组
2x + 3y = 52
x = y + 1
①
②
2 x + 3y = 52
x = y + 1
(y+1)
把②代入①得:
解得 y = 10
把y = 10代入②,得
x = y +1 = 10+ 1 = 11
∴方程组的解是
x = 11
y = 10
2(y + 1) +3y= 52
注意:
1.整体代入打括号
2.代入方程①和②都能求出另一个未知数的解,为了计算简便,选择代入方程②进行计算
(1)
y = x - 1
2x + 3y =7
练习:解方程组
∴原方程组的解为
y = 1
x = 2
①
②
(2)
2y - x = 5
x = 5 - 3y
①
②
∴原方程组的解为
y = 2
x = -1
变式 解方程组
2x + 3y = 52
①
②
解:
由②得:
x = y + 1 ③
把③代入①得:
解得 y = 10
把y = 10代入③,得
x = y +1 = 10+ 1 = 11
∴方程组的解是
x = 11
y = 10
2(y + 1) +3y= 52
x - y = 1
思考:能否将方程②用含x的式子表示 y,代入方程①求解?
变式 解方程组
①
②
③
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
4、把这个未知数的值代入上面变形的式子,求得另一个未知数的值;
5、写出方程组的解。
步骤归纳:
变
代、
回代
写解
2x + 3y = 52
x - y = 1
解:
由②得:
x = y + 1
把③代入①得:
2(y + 1) +3y= 52
把y= 10 代入 ③,得
x = y +1 = 10+ 1 = 11
解得 y = 10
∴方程组的解是
x =11
y = 10
解、
3、解一个一元一次方程,求得一个未知数的值;
该方法解二元一次方程组的一般步骤依次为:
思考:
1.该方法的核心步骤是哪一步?
2.该步骤的目的是什么?
3.请结合该方法的解方程思路,给该方法命名。
“代”。将一个未知数表示另一未知数的式子,代入另一方程
“消元”,将方程从二元变为一元
“代入消元法”。
变
代
解
回代
写解
代入消元法的概念:把二元一次方程组中一个方程的一个未知数用含另一未知数的式子表示出来,再代入另一方程,实现消元,进而求得这个二元一次方程组的解。这种方法叫做代入消元法,简称代入法。
用代入法解下列二元一次方程组
⑴
2x - y =3
3x + 2y =8
⑵
2x - y = 5
3x + 4y =2
⑴
2x - y = 3
3x - 2y = 8
②
①
把 ③ 代入 ① 得
3x- 2(2x-3)= 8
解得 x = -2
把 x = -2 代入 ③ 得
y=2×(-2)-3= -7
∴原方程组的解为
x = -2
y = -7
解:由 ② 得 y = 2x-3 ③
①
②
⑵
2x - y = 5
3x + 4y = 2
温馨提示
变形技巧:选择系数比较简单的方程进行变形.如果存在系数为“1”或者“-1”的未知数,选择该未知数来被表示。
基本思路:
变形技巧:
选择系数比较简单的方程进行变形。
一元一次方程
二元一次方程组
转化
消 元
一般步骤:
变
代
解
回代
写解
代入消元法的概念:
由二元一次方程组中一个方程,将一个未知数用含另一未知数的式子表示出来,再代入另一方程,实现消元,进而求得这个二元一次方程组的解。这种方法叫做代入消元法,简称代入法
主要思想:
“消元”思想
A层
1.在教材93页上完成练习2
2.作业本上完成教材97页2题
B层
2、如果∣y + 3x - 2∣+∣5x + 2y -2∣=0,求 x 、y的 值.
1、若方程5x 2m+n+4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家 笛卡儿
名人语录名人语录
谢谢聆听
8.2.1消元——解二元一次方程组
问题1:把下列方程写成用含x的式子表示y的形式和用含y的式子表示x的形式
“雪糕”问题
超市有2元和3元两种雪糕,陈老师准备买雪糕来奖励给班上上课积极的同学,由于单买一种雪糕,数量不够,所以两种同时购买,一共花费了52元,其中2元的雪糕数量比3元的雪糕数量多1,请问陈老师购买的两种雪糕各有多少支?
同学们,你们能用一元一次方程解决这个“雪糕”问题吗?
解:设2元的雪糕数量为x支,则3元的雪糕数量为(x-1)支。
由题意可得方程
2x + 3(x-1) = 52
解得 x = 11
则 x-1 = 11-1 = 10
答:陈老师购买的2元的雪糕有11支,3元的雪糕有10支。
你能列二元一次方程组解决这个问题吗?
解:2元的雪糕数量为x支,3元的雪糕数量为y支
由题意可得方程组
“雪糕”问题
超市有2元和3元两种雪糕,陈老师准备买雪糕来奖励给班上上课积极的同学,由于单买一种雪糕,数量不够,所以两种同时购买,一共花费了52元,其中2元的雪糕数量比3元的雪糕数量多1,请问陈老师购买的两种雪糕各有多少支?
如何解这个二元一次方程组解决呢 ?
分析:
2元雪糕总费用+3元雪糕总费用=52
2元雪糕数量=3元雪糕数量+1
例1 解方程组
2x + 3y = 52
x = y + 1
①
②
分析:该方程组中,方程②是用含 的式子表示 。
能。方程②是用含y的式子表示x,可将方程①中的x看成y+1,此时方程①就只剩下y一个未知数,即为一元一次方程。
y
x
小组讨论:
1.方程①中的x能否也用方程②中含y的式子来表示,为什么?
2.能否将该方程组变为一元一次方程进行求解,为什么?
能。因为方程组的解是两个方程的公共解,同一个未知数的值相等。
分析
解:
例1 解方程组
2x + 3y = 52
x = y + 1
①
②
2 x + 3y = 52
x = y + 1
(y+1)
把②代入①得:
解得 y = 10
把y = 10代入②,得
x = y +1 = 10+ 1 = 11
∴方程组的解是
x = 11
y = 10
2(y + 1) +3y= 52
注意:
1.整体代入打括号
2.代入方程①和②都能求出另一个未知数的解,为了计算简便,选择代入方程②进行计算
(1)
y = x - 1
2x + 3y =7
练习:解方程组
∴原方程组的解为
y = 1
x = 2
①
②
(2)
2y - x = 5
x = 5 - 3y
①
②
∴原方程组的解为
y = 2
x = -1
变式 解方程组
2x + 3y = 52
①
②
解:
由②得:
x = y + 1 ③
把③代入①得:
解得 y = 10
把y = 10代入③,得
x = y +1 = 10+ 1 = 11
∴方程组的解是
x = 11
y = 10
2(y + 1) +3y= 52
x - y = 1
思考:能否将方程②用含x的式子表示 y,代入方程①求解?
变式 解方程组
①
②
③
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
4、把这个未知数的值代入上面变形的式子,求得另一个未知数的值;
5、写出方程组的解。
步骤归纳:
变
代、
回代
写解
2x + 3y = 52
x - y = 1
解:
由②得:
x = y + 1
把③代入①得:
2(y + 1) +3y= 52
把y= 10 代入 ③,得
x = y +1 = 10+ 1 = 11
解得 y = 10
∴方程组的解是
x =11
y = 10
解、
3、解一个一元一次方程,求得一个未知数的值;
该方法解二元一次方程组的一般步骤依次为:
思考:
1.该方法的核心步骤是哪一步?
2.该步骤的目的是什么?
3.请结合该方法的解方程思路,给该方法命名。
“代”。将一个未知数表示另一未知数的式子,代入另一方程
“消元”,将方程从二元变为一元
“代入消元法”。
变
代
解
回代
写解
代入消元法的概念:把二元一次方程组中一个方程的一个未知数用含另一未知数的式子表示出来,再代入另一方程,实现消元,进而求得这个二元一次方程组的解。这种方法叫做代入消元法,简称代入法。
用代入法解下列二元一次方程组
⑴
2x - y =3
3x + 2y =8
⑵
2x - y = 5
3x + 4y =2
⑴
2x - y = 3
3x - 2y = 8
②
①
把 ③ 代入 ① 得
3x- 2(2x-3)= 8
解得 x = -2
把 x = -2 代入 ③ 得
y=2×(-2)-3= -7
∴原方程组的解为
x = -2
y = -7
解:由 ② 得 y = 2x-3 ③
①
②
⑵
2x - y = 5
3x + 4y = 2
温馨提示
变形技巧:选择系数比较简单的方程进行变形.如果存在系数为“1”或者“-1”的未知数,选择该未知数来被表示。
基本思路:
变形技巧:
选择系数比较简单的方程进行变形。
一元一次方程
二元一次方程组
转化
消 元
一般步骤:
变
代
解
回代
写解
代入消元法的概念:
由二元一次方程组中一个方程,将一个未知数用含另一未知数的式子表示出来,再代入另一方程,实现消元,进而求得这个二元一次方程组的解。这种方法叫做代入消元法,简称代入法
主要思想:
“消元”思想
A层
1.在教材93页上完成练习2
2.作业本上完成教材97页2题
B层
2、如果∣y + 3x - 2∣+∣5x + 2y -2∣=0,求 x 、y的 值.
1、若方程5x 2m+n+4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家 笛卡儿
名人语录名人语录
谢谢聆听
