人教版七年级下册8.2 二元一次方程组特殊解法 课件(共23张)
文档属性
| 名称 | 人教版七年级下册8.2 二元一次方程组特殊解法 课件(共23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 09:18:33 | ||
图片预览








文档简介
(共23张PPT)
课前教师寄语:
不识庐山真面目,只缘身在此山中。
——宋-苏轼 《题西林壁》
二元一次方程组特殊解法
——整体思想的运用
整体思想
从问题的整体性质出发,突出问题的整体结构的分析和改造,发现问题的整体结构特征,善于用”集成“的眼光,把某些式子或图形看成一个整体,把握它们之间的关联,进行有目的、有意识的整体处理。
温故知新
归纳:二元一次方程组的常规解法,是代入消元法和加减消元法。
这两种方法都是从“消元”这个基本思想出发,先把“二元”转化为“一元”把解二元一次方程组的问题归结为解一元一次方程,在“消元”法中,包含了“未知”转化到“已知”的重要数学化归思想。
1、解二元一次方程组的基本思想是什么?
2、消元的方法有哪些?
3、什么情况下用代入法简单?什么情况下用消元法简单?
学习目标
1、进一步体会代入法、加减法解二元一次方程组的实质;
2、通过观察,会灵活运用“整体思想”方法求解结构比较特殊的二元一次方程组。(重点、难点)
思考探究
一、特殊消元法之“代入”利器——整体代入
解方程组
例1-1、
①
②
整体代入
得到
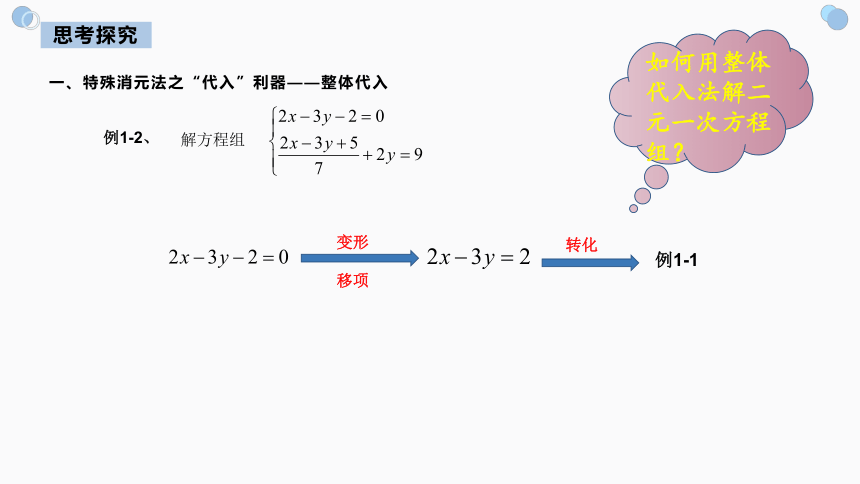
思考探究
一、特殊消元法之“代入”利器——整体代入
解方程组
例1-2、
变形
移项
转化
例1-1
如何用整体代入法解二元一次方程组?
拔高训练:
已知 ,解方程 。
思考探究
一、特殊消元法之“代入”利器——整体代入
提取公因数3
整体代入
转化
变形
构造方程组
求解
思考探究
二、特殊消元法之整体换元
例2、
思考1:什么时候用整体换元法?
解:设a+b=m,a-b=n.
则原方程组可化为
思考2:用整体换元法需要注意什么?
思考探究
二、特殊消元法之整体换元
例2、
二元一次方程组的解只与方程组的系数有关,与所选用的未知数无关。
思考3:通过以上两个问题,你又发现了什么?
思考探究
二、特殊消元法之整体换元
拔高训练:
1、已知关于x,y的方程组 的解是 ,
(1)求关于m,n 的方程组的解;
思考探究
二、特殊消元法之整体换元
拔高训练:
1、已知关于x,y的方程组 的解是 ,
(2)求关于m,n 的方程组的解。
两边同时除以3
转化
未知
已知
化归思想
思考探究
二、特殊消元法之整体换元
拔高训练:
2、解方程组:
思考探究
三、特殊消元法之直接整体加减
例3-1、
解方程组:
例3-2、
解方程组:
为什么可以这样做,你发现了什么?
拔高训练:
1、已知方程组 的解也满足 ,求m的值。
①
②
代入
①+②
①—②
方法一:
拔高训练:
1、已知方程组 的解也满足 ,求m的值。
①
②
变形、整体相加
代入
方法一:
拔高训练:
2、已知方程组 的解也满足 ,求m的值。
①
②
①+②
代入
整体相加
拔高训练:
3、已知方程组 的解也满足 ,求m的值。
①
②
①—②
联立构造方程组
整体相减
课下思考:
5、已知方程组 的解也满足 ,求m的值。
课下尝试不同解法
课堂小结:
整体思想在解二元一次方程组中的应用
1、整体代入法
2、整体换元法
3、整体加减法
半山腰总是挤的,你得去山顶看看~
教师寄语:
本节课启示:
缺少整体思想,行为及能力也就有了局限性。想要认识事情真实面目,只有打破局限,走到更远更广阔的地方,才能看清事情的本来面貌。
谢谢大家~
课前教师寄语:
不识庐山真面目,只缘身在此山中。
——宋-苏轼 《题西林壁》
二元一次方程组特殊解法
——整体思想的运用
整体思想
从问题的整体性质出发,突出问题的整体结构的分析和改造,发现问题的整体结构特征,善于用”集成“的眼光,把某些式子或图形看成一个整体,把握它们之间的关联,进行有目的、有意识的整体处理。
温故知新
归纳:二元一次方程组的常规解法,是代入消元法和加减消元法。
这两种方法都是从“消元”这个基本思想出发,先把“二元”转化为“一元”把解二元一次方程组的问题归结为解一元一次方程,在“消元”法中,包含了“未知”转化到“已知”的重要数学化归思想。
1、解二元一次方程组的基本思想是什么?
2、消元的方法有哪些?
3、什么情况下用代入法简单?什么情况下用消元法简单?
学习目标
1、进一步体会代入法、加减法解二元一次方程组的实质;
2、通过观察,会灵活运用“整体思想”方法求解结构比较特殊的二元一次方程组。(重点、难点)
思考探究
一、特殊消元法之“代入”利器——整体代入
解方程组
例1-1、
①
②
整体代入
得到
思考探究
一、特殊消元法之“代入”利器——整体代入
解方程组
例1-2、
变形
移项
转化
例1-1
如何用整体代入法解二元一次方程组?
拔高训练:
已知 ,解方程 。
思考探究
一、特殊消元法之“代入”利器——整体代入
提取公因数3
整体代入
转化
变形
构造方程组
求解
思考探究
二、特殊消元法之整体换元
例2、
思考1:什么时候用整体换元法?
解:设a+b=m,a-b=n.
则原方程组可化为
思考2:用整体换元法需要注意什么?
思考探究
二、特殊消元法之整体换元
例2、
二元一次方程组的解只与方程组的系数有关,与所选用的未知数无关。
思考3:通过以上两个问题,你又发现了什么?
思考探究
二、特殊消元法之整体换元
拔高训练:
1、已知关于x,y的方程组 的解是 ,
(1)求关于m,n 的方程组的解;
思考探究
二、特殊消元法之整体换元
拔高训练:
1、已知关于x,y的方程组 的解是 ,
(2)求关于m,n 的方程组的解。
两边同时除以3
转化
未知
已知
化归思想
思考探究
二、特殊消元法之整体换元
拔高训练:
2、解方程组:
思考探究
三、特殊消元法之直接整体加减
例3-1、
解方程组:
例3-2、
解方程组:
为什么可以这样做,你发现了什么?
拔高训练:
1、已知方程组 的解也满足 ,求m的值。
①
②
代入
①+②
①—②
方法一:
拔高训练:
1、已知方程组 的解也满足 ,求m的值。
①
②
变形、整体相加
代入
方法一:
拔高训练:
2、已知方程组 的解也满足 ,求m的值。
①
②
①+②
代入
整体相加
拔高训练:
3、已知方程组 的解也满足 ,求m的值。
①
②
①—②
联立构造方程组
整体相减
课下思考:
5、已知方程组 的解也满足 ,求m的值。
课下尝试不同解法
课堂小结:
整体思想在解二元一次方程组中的应用
1、整体代入法
2、整体换元法
3、整体加减法
半山腰总是挤的,你得去山顶看看~
教师寄语:
本节课启示:
缺少整体思想,行为及能力也就有了局限性。想要认识事情真实面目,只有打破局限,走到更远更广阔的地方,才能看清事情的本来面貌。
谢谢大家~
