人教版七年级下册8.3 实际问题与二元一次方程组 课件(共17张)
文档属性
| 名称 | 人教版七年级下册8.3 实际问题与二元一次方程组 课件(共17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
8.3实际问题与二元一次方程组
人教版初中数学
七年级下册第八章
审题,弄清____ ,及题中的 ;
设未知数,可 ,也可 ;
根据题目中所给的关系找出 ,列出方程;
,检验解的正确性;
题意
直接设元
间接设元
相等关系
解方程组
相等关系
1.列方程组解应用题的一般步骤:
复 习
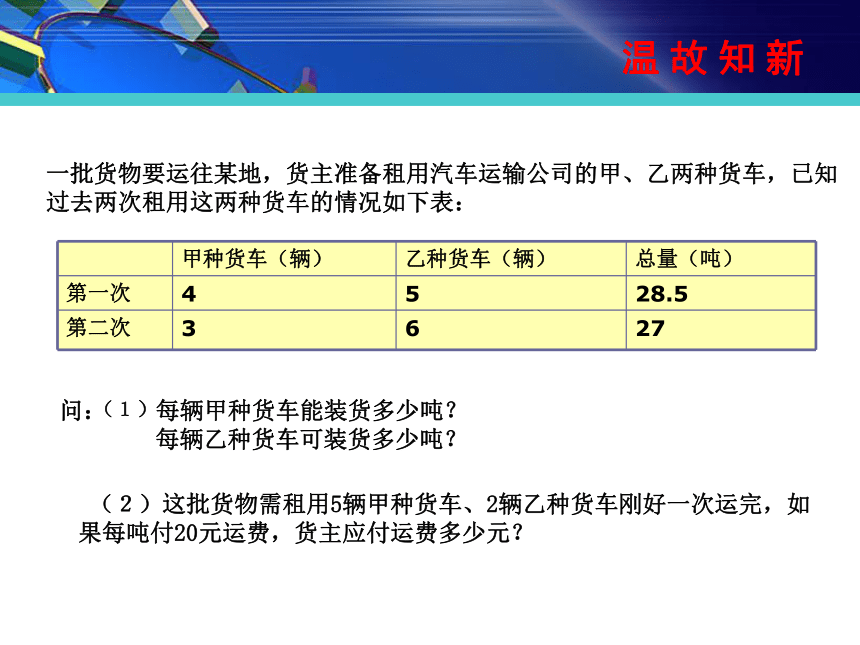
一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车的情况如下表:
问: 每辆甲种货车能装货多少吨?
每辆乙种货车可装货多少吨?
温 故 知 新
甲种货车(辆) 乙种货车(辆) 总量(吨)
第一次 4 5 28.5
第二次 3 6 27
(2)这批货物需租用5辆甲种货车、2辆乙种货车刚好一次运完,如果每吨付20元运费,货主应付运费多少元?
(1)
1、在这道题目中,有部分条件是以表格的形式给出的,
这就要求同学们在审题时要真正读懂表中的信息,这样才
能找到解题的方向。
2、本题中的单位运价是每吨20元,有时,单位运价还可
以以下面的形式出现。
回顾思考
长青化工厂与A地相距150千米,工厂要将200吨货物用
汽车运往A地,已知公路运价是1.5元/(吨·千米),则
需付运费_________元.
45000
想 一 想
运费=货物重量×公路里程×运价
200×150×1.5=45000
探究新知
探 究 1
探 究 2
探 究 3
巩固提高
探究1:
长青化工厂用汽车从A地购买一批原料运回工厂,
制成产品后用火车运到B地。工厂与A地相距80千米,
与B地相距150千米。公路运价为1.5元/(吨·千米),
铁路运价为1.2元/(吨·千米),这两次运输支出公路运费15000元,铁路运费97200元。求工厂从A地购得的原料有多少吨?制成的产品有多少吨?
运输路线单一化问题
探究新知
这道题中的量有很多,不妨我们画一个示意图。
A地
B地
长青化工厂
公路80km
铁路150km
原料
产品
1.5元/(吨·千米)
1.2元/(吨·千米)
公路运费:15000元 铁路运费:97200元
画出示意图是解决道路运输问题的手段之一。
探究新知
如图8.3-2,长青化工厂与A,B两地有公路、 铁路
相连。这家工厂从A地购买一批原料运回工厂,制成产品运
B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/
(吨·千米),这两次运输共支出公路运费15000元,铁路
运费97200元。
问:购得的原料有多少吨? 制成的产品有多少吨?
探究2:
探究新知
运输路线复杂化问题
原料x吨 产品y吨 合计
公路运费(元)
铁路运费(元)
列表分析是解决道路运输问题的另一手段。
探究2:
探究新知
问: 购得的原料有多少吨?制成的产品有多少吨?
如图8.3-2,长青化工厂与A,B两地有公路、铁路相连。这家工厂从A地购买一批原料运回工厂,制成产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。
探究3:
(2)若原料每吨1000元,制成的产品每吨8000 元,这批
产品的销售款比原料费与运输费的和多多少元?
(1)
探究新知
毛利润 = 销售款-(原料费+运输费)
产品价值=产品重量×产品单价
原料价值=原料重量×原料单价
探究3:
探究新知
北京和上海都有某种仪器可供外地使用。其中北京可提供10台,上海可提供4台。已知重庆需要8台,武汉需要6台,从北京、上海将仪器运往重庆、武汉的费用如下表所示。有关部门计划用8000元运送这些仪器,请你设计一种方案,使武汉、重庆能得到所需仪器,而且运费正好够用。
课堂练习 反馈调控
终点 起点 武汉 重庆
北京 400 800
上海 300 500
运费表
单位:元/台
400元
400(10-x)元
重庆需要8台
武需要6台
上海4台
800元
500元
300元
800x元
500y元
300(4-y )元
北京10台
武汉需要6台
课堂练习 反馈调控
课堂小结 知识梳理
设未知数
列方程组
解 方 程 组
代入法
加减法
(消元)
实际问题的答案
检验
数学问题的解
(二元一次方程组的解)
数学问题
(二元一次方程组)
实际问题
学生思考 、讨论、整理
布置作业
1、必做题 P116 第2题、第6题
2、选做题 P117 第9题
谢谢聆听
8.3实际问题与二元一次方程组
人教版初中数学
七年级下册第八章
审题,弄清____ ,及题中的 ;
设未知数,可 ,也可 ;
根据题目中所给的关系找出 ,列出方程;
,检验解的正确性;
题意
直接设元
间接设元
相等关系
解方程组
相等关系
1.列方程组解应用题的一般步骤:
复 习
一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车的情况如下表:
问: 每辆甲种货车能装货多少吨?
每辆乙种货车可装货多少吨?
温 故 知 新
甲种货车(辆) 乙种货车(辆) 总量(吨)
第一次 4 5 28.5
第二次 3 6 27
(2)这批货物需租用5辆甲种货车、2辆乙种货车刚好一次运完,如果每吨付20元运费,货主应付运费多少元?
(1)
1、在这道题目中,有部分条件是以表格的形式给出的,
这就要求同学们在审题时要真正读懂表中的信息,这样才
能找到解题的方向。
2、本题中的单位运价是每吨20元,有时,单位运价还可
以以下面的形式出现。
回顾思考
长青化工厂与A地相距150千米,工厂要将200吨货物用
汽车运往A地,已知公路运价是1.5元/(吨·千米),则
需付运费_________元.
45000
想 一 想
运费=货物重量×公路里程×运价
200×150×1.5=45000
探究新知
探 究 1
探 究 2
探 究 3
巩固提高
探究1:
长青化工厂用汽车从A地购买一批原料运回工厂,
制成产品后用火车运到B地。工厂与A地相距80千米,
与B地相距150千米。公路运价为1.5元/(吨·千米),
铁路运价为1.2元/(吨·千米),这两次运输支出公路运费15000元,铁路运费97200元。求工厂从A地购得的原料有多少吨?制成的产品有多少吨?
运输路线单一化问题
探究新知
这道题中的量有很多,不妨我们画一个示意图。
A地
B地
长青化工厂
公路80km
铁路150km
原料
产品
1.5元/(吨·千米)
1.2元/(吨·千米)
公路运费:15000元 铁路运费:97200元
画出示意图是解决道路运输问题的手段之一。
探究新知
如图8.3-2,长青化工厂与A,B两地有公路、 铁路
相连。这家工厂从A地购买一批原料运回工厂,制成产品运
B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/
(吨·千米),这两次运输共支出公路运费15000元,铁路
运费97200元。
问:购得的原料有多少吨? 制成的产品有多少吨?
探究2:
探究新知
运输路线复杂化问题
原料x吨 产品y吨 合计
公路运费(元)
铁路运费(元)
列表分析是解决道路运输问题的另一手段。
探究2:
探究新知
问: 购得的原料有多少吨?制成的产品有多少吨?
如图8.3-2,长青化工厂与A,B两地有公路、铁路相连。这家工厂从A地购买一批原料运回工厂,制成产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。
探究3:
(2)若原料每吨1000元,制成的产品每吨8000 元,这批
产品的销售款比原料费与运输费的和多多少元?
(1)
探究新知
毛利润 = 销售款-(原料费+运输费)
产品价值=产品重量×产品单价
原料价值=原料重量×原料单价
探究3:
探究新知
北京和上海都有某种仪器可供外地使用。其中北京可提供10台,上海可提供4台。已知重庆需要8台,武汉需要6台,从北京、上海将仪器运往重庆、武汉的费用如下表所示。有关部门计划用8000元运送这些仪器,请你设计一种方案,使武汉、重庆能得到所需仪器,而且运费正好够用。
课堂练习 反馈调控
终点 起点 武汉 重庆
北京 400 800
上海 300 500
运费表
单位:元/台
400元
400(10-x)元
重庆需要8台
武需要6台
上海4台
800元
500元
300元
800x元
500y元
300(4-y )元
北京10台
武汉需要6台
课堂练习 反馈调控
课堂小结 知识梳理
设未知数
列方程组
解 方 程 组
代入法
加减法
(消元)
实际问题的答案
检验
数学问题的解
(二元一次方程组的解)
数学问题
(二元一次方程组)
实际问题
学生思考 、讨论、整理
布置作业
1、必做题 P116 第2题、第6题
2、选做题 P117 第9题
谢谢聆听
