7.2万有引力定律(共20张PPT)
文档属性
| 名称 | 7.2万有引力定律(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-11 12:09:29 | ||
图片预览








文档简介
(共20张PPT)
02.万有引力定律
是什么原因使行星绕太阳运动?
伽利略:行星是依靠惯性自行维持的运动。
开普勒:行星是受到了来自太阳的类似于磁力的作用,与距离成反比。
笛卡儿:在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动。
胡克和哈雷等人认为:行星绕太阳运动是因为受到了太阳对它的引力,甚至证明了如果行星的轨道是圆形的,它所受引力的大小跟行星到太阳的距离的二次方成反比。
局限性:但是他们由于对关于运动和力的概念还不清晰,因此他们无法深入研究。
直到牛顿的出现,牛顿第一定律提出:力是改变运动状态的原因,行星的运动需要力。这就是说,使行星沿圆或椭圆运动,需要指向圆心或椭圆焦点的力,这个力应该就是太阳对它的引力。于是,牛顿利用他的运动定律把行星的向心加速度与太阳对它的引力联系起来了。
牛顿在前人研究的基础上,凭借其超凡的数学能力和坚定的信念,深入研究,最终发现了万有引力定律。
如果说我看的比别人更远,那是因为我站在巨人的肩膀上。
——牛顿
到底是什么原因使行星绕太阳运动 让我们来揭开它们神秘的面纱。
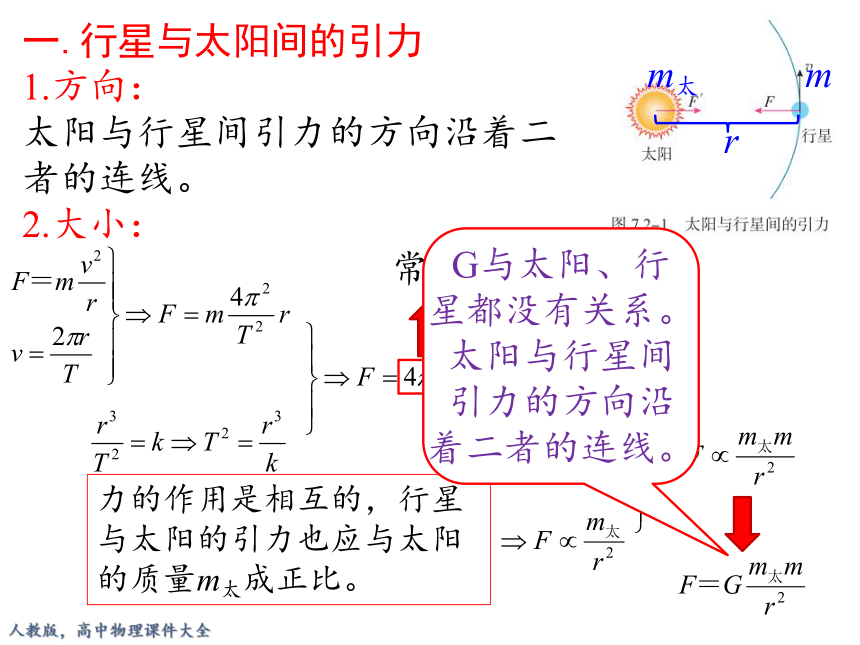
一.行星与太阳间的引力
1.方向:
太阳与行星间引力的方向沿着二
者的连线。
2.大小:
m太 m
r
常量
力的作用是相互的,行星与太阳的引力也应与太阳的质量m太成正比。
G与太阳、行星都没有关系。太阳与行星间引力的方向沿着二者的连线。
一.行星与太阳间的引力
理论上这个结论只适用于行星与太阳之间,但牛顿又想,地球绕太阳运动,月球绕地球运动,它们之间的作用力是同一种性质的力吗?这种力与地球对树上苹果的吸引力也是同一种性质的力吗?
二.月地检验
已知地球半径为R=6.37×106m,重力加速度g=9.8m/s2,月地距离r≈60R≈3.84×108m,月球周期27.3天。
思路:
检验:
月地检验表明,地面物体所受地
球的引力、月球所受地球的引力,
与太阳、行星间的引力,真的遵
从相同的规律!
我们的思想还可以更解放。既然太阳与行星之间、地球与月球之间,以及地球与地面物体之间具有“与两个物体的质量成正比、与它们之间距离的二次方成反比”的吸引力,是否任意两个物体之间都有这样的力呢?很可能有,只是由于身边物体的质量比天体的质量小得多,不易觉察罢了。于是我们大胆地把以上结论推广到宇宙中的一切物体之间:
三.万有引力定律
内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m1和m2的乘积成正比、与它们之间距离r的二次方成反比,即:
它于1687年发表在牛顿的传世之作《自然哲学的数学原理》中。
对万有引力的理解
(1)普遍性:任何两个物体之间都存在引力(大到天体小到微观粒子),万有引力是自然界中物体间的基本相互作用之一。
(2)相互性:万有引力具有相互性,符合牛顿第三定律。
(3)宏观性:只有在质量巨大的天体间或天体与物体间它的存在才有宏观的物理意义。在微观世界中,万有引力可以忽略不计。地球表面物体受力时,也不考虑万有引力。
三.万有引力定律
内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m1和m2的乘积成正比、与它们之间距离r的二次方成反比,即:
适用条件:
①质点和可看成质点的物体。m为物体质量,r为物体间距离
②质量分布均匀的球体外部(天体之间)
注意:
r越大万有引力越小,而r 0,万有引力并不是无穷大,物体放在地球中心,万有引力为零。
1789年英国物理学家卡文迪许测出了引力常量:
G=6.67×10-11Nm2/kg2
意义:
用实验验证了万有引力的正确性。
使万有引力定律公式有了真正的实用价值。
开创了测量弱力的新时代,使放大思想得到推广。
四.引力常量
木星有4颗卫星是伽利略发现的,称为伽利略卫星,其中三颗卫星的周期之比为1∶2∶4。小华同学打算根据万有引力的知识计算木卫二绕木星运动的周期,她收集到了如下一些数据。
木卫二的数据:质量4.8×1022kg、绕木星做匀速圆周运动的轨道半径6.7×108m。
木星的数据:质量1.9×1027kg、半径7.1×107m、自转周期9.8h。
但她不知道应该怎样做,请你帮助她完成木卫二运动周期的计算。
算一算:太阳与地球之间的万有引力有多大?太阳的质量为M = 2.0×1030 kg,地球质量为m = 6.0×1024 kg,日、地之间的距离为r= 1.5×1011 m)
3.5×1022 N
这个力非常大,能够拉断直径为 9000 m 的钢柱。
例1. 要使两物体间的万有引力减小到原来的1/4,下列办法可采用的是( )
A. 使两个物体质量各减小一半,距离不变
B. 使其中一个物体的质量减小到原来的1/4,距离不变
C. 使两物体的距离增为原来的2倍,质量不变
D. 距离和两物体质量都减小为原来的1/4
ABC
例2.关于万有引力的说法,正确的有( )
A.物体落到地面上,说明地球对物体有引力,物体对地球没有引力
B.万有引力定律是牛顿在总结前人研究的基础上发现的
C.地面上自由下落的苹果和天空中运行的月亮,受到的都是地球的万有引力
D.F=Gm1m2/r2中的G是一个比例常数,是没有单位的
BC
例3.有一质量为M,半径为R,密度均匀的球体,在距离球心O为2R的地方有一质量为m的点,现在M中挖去一半径为R/2的球体,如图所示,求剩余部分对m的万有引力F剩为多大?
提示:割补法
答案:
五.重力与万有引力的关系
①若不考虑地球自转:
②实际上万有引力的一部分提供物
体做圆周运动的向心力,重力是万
有引力的另一个分力,故:
而且重力也并不指向地心(赤道两极除外)。
③实际上F向<④地球由于自转,地表物体角速度处处相同,赤道半径最大,做圆周运动所需向心力也最大,重力反而最小,随着纬度升高,向心力变小,重力变大,g变大
⑤随着高度增加, ,g变小
例4.假如地球自转速度增大,关于物体的重力,下列说法中正确的是 ( )
A.放在赤道地面上物体的万有引力不变
B.放在两极地面上物体的重力不变
C.放在赤道地面上物体的重力减小
D.放在两极地面上物体的重力增大
例5. 关于重力和万有引力的关系,错误的是( )
A.物体所受的重力就是万有引力
B.重力方向竖直向下,且一定指向地心
C.在粗略的计算中,可以认为重力等于万有引力
D.严格来说重力并不等于万有引力,除两极处的物体的重力等于万有引力外,在地球其他各处的重力都略小于万有引力
ABC
AB
例6.回答下列问题:
(1)地球半径为R,物体在地表重力是mg,则离地面高为R的地方重力是多少?如果把它放到地心,重力又是多少?
(2)地表重力加速度为g,则离地表3R处的重力加速度是多少?
例7.火星的半径是地球半径的一半,其质量是地球质量的1/9,一宇航员的质量是m,他在地球上能举起物体的最大质量是 m0。求这名宇航员:
(1)在火星上所受的重力是在地球上的多少倍?
(2)在火星上最多能举起质量多大的物体?
4/9,9 m0 /4
Mg/4,0
g/16
例8.若在某行星和地球上相对于各自的水平地面附近相同的高度处以相同的速度平抛一物体,它们在水平方向运动的距离之比为2:3,已知该行星质量约为地球的9倍,地球半径为R,由此可知,该行星的半径约为多少?
02.万有引力定律
是什么原因使行星绕太阳运动?
伽利略:行星是依靠惯性自行维持的运动。
开普勒:行星是受到了来自太阳的类似于磁力的作用,与距离成反比。
笛卡儿:在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动。
胡克和哈雷等人认为:行星绕太阳运动是因为受到了太阳对它的引力,甚至证明了如果行星的轨道是圆形的,它所受引力的大小跟行星到太阳的距离的二次方成反比。
局限性:但是他们由于对关于运动和力的概念还不清晰,因此他们无法深入研究。
直到牛顿的出现,牛顿第一定律提出:力是改变运动状态的原因,行星的运动需要力。这就是说,使行星沿圆或椭圆运动,需要指向圆心或椭圆焦点的力,这个力应该就是太阳对它的引力。于是,牛顿利用他的运动定律把行星的向心加速度与太阳对它的引力联系起来了。
牛顿在前人研究的基础上,凭借其超凡的数学能力和坚定的信念,深入研究,最终发现了万有引力定律。
如果说我看的比别人更远,那是因为我站在巨人的肩膀上。
——牛顿
到底是什么原因使行星绕太阳运动 让我们来揭开它们神秘的面纱。
一.行星与太阳间的引力
1.方向:
太阳与行星间引力的方向沿着二
者的连线。
2.大小:
m太 m
r
常量
力的作用是相互的,行星与太阳的引力也应与太阳的质量m太成正比。
G与太阳、行星都没有关系。太阳与行星间引力的方向沿着二者的连线。
一.行星与太阳间的引力
理论上这个结论只适用于行星与太阳之间,但牛顿又想,地球绕太阳运动,月球绕地球运动,它们之间的作用力是同一种性质的力吗?这种力与地球对树上苹果的吸引力也是同一种性质的力吗?
二.月地检验
已知地球半径为R=6.37×106m,重力加速度g=9.8m/s2,月地距离r≈60R≈3.84×108m,月球周期27.3天。
思路:
检验:
月地检验表明,地面物体所受地
球的引力、月球所受地球的引力,
与太阳、行星间的引力,真的遵
从相同的规律!
我们的思想还可以更解放。既然太阳与行星之间、地球与月球之间,以及地球与地面物体之间具有“与两个物体的质量成正比、与它们之间距离的二次方成反比”的吸引力,是否任意两个物体之间都有这样的力呢?很可能有,只是由于身边物体的质量比天体的质量小得多,不易觉察罢了。于是我们大胆地把以上结论推广到宇宙中的一切物体之间:
三.万有引力定律
内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m1和m2的乘积成正比、与它们之间距离r的二次方成反比,即:
它于1687年发表在牛顿的传世之作《自然哲学的数学原理》中。
对万有引力的理解
(1)普遍性:任何两个物体之间都存在引力(大到天体小到微观粒子),万有引力是自然界中物体间的基本相互作用之一。
(2)相互性:万有引力具有相互性,符合牛顿第三定律。
(3)宏观性:只有在质量巨大的天体间或天体与物体间它的存在才有宏观的物理意义。在微观世界中,万有引力可以忽略不计。地球表面物体受力时,也不考虑万有引力。
三.万有引力定律
内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m1和m2的乘积成正比、与它们之间距离r的二次方成反比,即:
适用条件:
①质点和可看成质点的物体。m为物体质量,r为物体间距离
②质量分布均匀的球体外部(天体之间)
注意:
r越大万有引力越小,而r 0,万有引力并不是无穷大,物体放在地球中心,万有引力为零。
1789年英国物理学家卡文迪许测出了引力常量:
G=6.67×10-11Nm2/kg2
意义:
用实验验证了万有引力的正确性。
使万有引力定律公式有了真正的实用价值。
开创了测量弱力的新时代,使放大思想得到推广。
四.引力常量
木星有4颗卫星是伽利略发现的,称为伽利略卫星,其中三颗卫星的周期之比为1∶2∶4。小华同学打算根据万有引力的知识计算木卫二绕木星运动的周期,她收集到了如下一些数据。
木卫二的数据:质量4.8×1022kg、绕木星做匀速圆周运动的轨道半径6.7×108m。
木星的数据:质量1.9×1027kg、半径7.1×107m、自转周期9.8h。
但她不知道应该怎样做,请你帮助她完成木卫二运动周期的计算。
算一算:太阳与地球之间的万有引力有多大?太阳的质量为M = 2.0×1030 kg,地球质量为m = 6.0×1024 kg,日、地之间的距离为r= 1.5×1011 m)
3.5×1022 N
这个力非常大,能够拉断直径为 9000 m 的钢柱。
例1. 要使两物体间的万有引力减小到原来的1/4,下列办法可采用的是( )
A. 使两个物体质量各减小一半,距离不变
B. 使其中一个物体的质量减小到原来的1/4,距离不变
C. 使两物体的距离增为原来的2倍,质量不变
D. 距离和两物体质量都减小为原来的1/4
ABC
例2.关于万有引力的说法,正确的有( )
A.物体落到地面上,说明地球对物体有引力,物体对地球没有引力
B.万有引力定律是牛顿在总结前人研究的基础上发现的
C.地面上自由下落的苹果和天空中运行的月亮,受到的都是地球的万有引力
D.F=Gm1m2/r2中的G是一个比例常数,是没有单位的
BC
例3.有一质量为M,半径为R,密度均匀的球体,在距离球心O为2R的地方有一质量为m的点,现在M中挖去一半径为R/2的球体,如图所示,求剩余部分对m的万有引力F剩为多大?
提示:割补法
答案:
五.重力与万有引力的关系
①若不考虑地球自转:
②实际上万有引力的一部分提供物
体做圆周运动的向心力,重力是万
有引力的另一个分力,故:
而且重力也并不指向地心(赤道两极除外)。
③实际上F向<
⑤随着高度增加, ,g变小
例4.假如地球自转速度增大,关于物体的重力,下列说法中正确的是 ( )
A.放在赤道地面上物体的万有引力不变
B.放在两极地面上物体的重力不变
C.放在赤道地面上物体的重力减小
D.放在两极地面上物体的重力增大
例5. 关于重力和万有引力的关系,错误的是( )
A.物体所受的重力就是万有引力
B.重力方向竖直向下,且一定指向地心
C.在粗略的计算中,可以认为重力等于万有引力
D.严格来说重力并不等于万有引力,除两极处的物体的重力等于万有引力外,在地球其他各处的重力都略小于万有引力
ABC
AB
例6.回答下列问题:
(1)地球半径为R,物体在地表重力是mg,则离地面高为R的地方重力是多少?如果把它放到地心,重力又是多少?
(2)地表重力加速度为g,则离地表3R处的重力加速度是多少?
例7.火星的半径是地球半径的一半,其质量是地球质量的1/9,一宇航员的质量是m,他在地球上能举起物体的最大质量是 m0。求这名宇航员:
(1)在火星上所受的重力是在地球上的多少倍?
(2)在火星上最多能举起质量多大的物体?
4/9,9 m0 /4
Mg/4,0
g/16
例8.若在某行星和地球上相对于各自的水平地面附近相同的高度处以相同的速度平抛一物体,它们在水平方向运动的距离之比为2:3,已知该行星质量约为地球的9倍,地球半径为R,由此可知,该行星的半径约为多少?
