北师大版六年级下册数学 第四单元 正比例和反比例 测试卷 (含答案)
文档属性
| 名称 | 北师大版六年级下册数学 第四单元 正比例和反比例 测试卷 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 139.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 15:47:32 | ||
图片预览




文档简介
单元测试卷(含答案)
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 总分
得分
一、填空题(共36分)
1.(本题2分)圆的周长一定,圆周率和它的直径( )。(在括号里填“成正比例”“成反比例”或“不成比例”)。
2.(本题2分)如果x∶4=5∶y,那么x和y成________比例。
3.(本题6分)在平行四边形里,底一定,面积和高 比例
高一定,面积和底 比例
面积一定,底和高 比例.
4.(本题6分)用x、y表示长方形相邻两边的长,下表是面积为36cm2的长方形相邻两边长度的变化关系。请把表格填完整,再填空。
x 1 2 3 4 6
y 36 ( ) 12 ( ) ( )
①x与y成( )比例。
②当x=2.5时,y=( )时,当x=时,y=( )。
5.(本题8分)已知x和y是成正比例的两个量,请把下表填写完整。
x 0.8 0.5 10
y 1.2 24
6.(本题6分)慢车和快车沿相同的路线从地到地所行路程和时间的关系如图所示:
(1)慢车行驶时间和路程成( )比例关系。
(2)快车追上慢车所需时间是( )小时。
(3)、两地之间的路程是( )千米。
7.(本题3分)总价一定,购买的练习本的本数和( )成反比例。
8.(本题3分)一个油厂用200千克黄豆可榨26千克油,照这样计算,5吨黄豆可榨油( )千克.
二、判断题(共12分)
9.(本题2分)同一时间、同一地点,物体的影长与物体的高度成正比例关系.( )
10.(本题2分)圆的半径和周长成正比例关系。( )
11.(本题2分)分子一定,分母和分数值成反比例.( )
12.(本题2分)圆周长一定,直径和π成反比例。( )
13.(本题2分)在,如果V一定,则S与h成反比例。( )
三、选择题(共10分)
14.(本题2分)表示x和y成正比例关系的式子是( )
A.x+y=6 B.x﹣y=8 C.y=5x D.xy=7
15.(本题2分)下面图象中,表示甲、乙两个量成正比例关系的有( )。
A.①② B.③④ C.①③ D.②④
16.(本题2分)下面各选项中的两个量不成反比例的是( )。
A.行驶的路程一定,车轮的周长与车轮需要转动的圈数。 B.三角形的面积一定,它的底和高。
C.小东从家步行到学校,已走的路程和剩下的路程。 D.小东从家步行到学校的平均速度与所花的时间。
17.(本题2分)a与b成正比例,并且当a=1.5时,b=0.15,那么当a=2.5时,b=( )。
A.25 B.2.5 C.0.25
18.(本题2分)如下图所示,一个大长方形被两条线段分成四个小长方形。如果其中图形A、B、C的面积分别是2cm2、4cm2和5cm2那么阴影部分的面积为( )cm2。
A.1 B. C. D.
四、解答题(共42分)
19.(本题12分)判断下面各题中的两种量是否成正比例,并说明理由。
(1)工作效率一定,工作时间和工作总量。
(2)圆的周长和直径。
(3)比例尺一定,图上距离和实际距离。
(4)减数一定,被减数和差。
20.(本题9分)一些长方形的长与宽的长度变化如表.
长/厘米 5 7.5 10 12.5 15 17.5 …
宽/厘米 2 3 4 5 6 7 …
(1)这些长方形的宽与长成 比例.如果用y表示长,x表示宽,则y= .
(2)若长方形的宽是8厘米,长是 厘米:若长是8厘米,宽是 厘米.
(3)这样的长方形中,当周长是70厘米时,它的长和宽各是多少?(列式解答)
21.(本题9分)一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。
时间/时 1 2 3 4 5 6
路程/km 90 180 270
(1)把下表填写完整。
(2)你发现了什么?
(3)路程与时间成正比例吗?
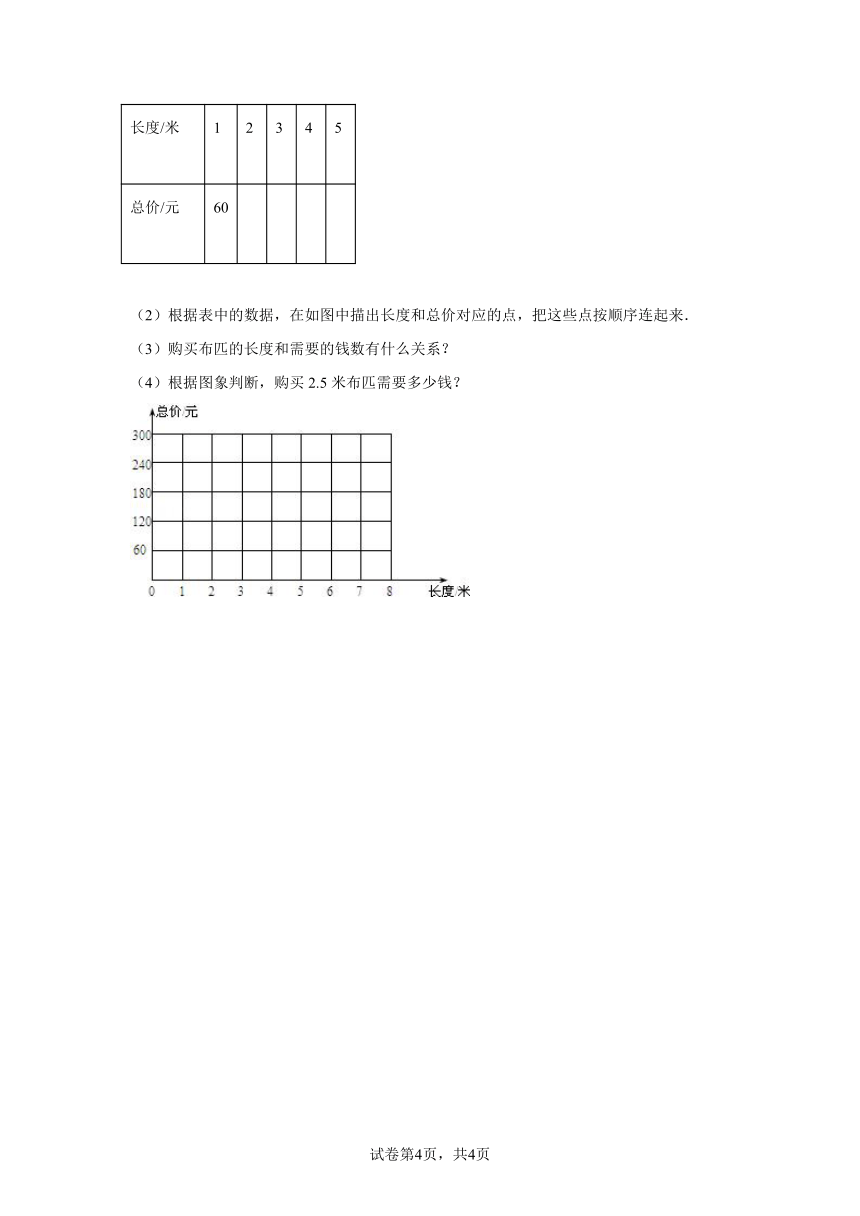
22.(本题12分)一种服装布料每米售价为60元,购买2米、3米、…各需要多少元?
(1)填写下表.
长度/米 1 2 3 4 5
总价/元 60
(2)根据表中的数据,在如图中描出长度和总价对应的点,把这些点按顺序连起来.
(3)购买布匹的长度和需要的钱数有什么关系?
(4)根据图象判断,购买2.5米布匹需要多少钱?
试卷第页,共页
试卷第页,共页
参考答案:
1.不成比例
【解析】
【分析】
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】
因为圆周率是一个固定不变的数,不能随着圆的直径的变化而变化,所以圆周率和圆的直径不成比例。
【点睛】
此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
2.反
【解析】
【分析】
根据比例的基本性质,外项积等于内项积,得到xy=4×5,x和y的乘积为定值,典型的反比例关系。
【详解】
xy=4×5=20
所以x和y成反比例。
【点睛】
满足反比例关系的两个量,必须满足乘积一定的基本条件,可以利用一般表达式xy=k来判断。
3.正,正,反.
【解析】
【详解】
试题分析:判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
解:因为平行四边形的面积÷高=底(一定),所以面积和高正比例;
因为平行四边形的面积÷底=高(一定),所以面积和底正比例;
因为平行四边形的底×高=面积(一定),所以底和高反比例;
点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
4. 18 9 6 反 14.4 108
【解析】
【分析】
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】
(1)因为1×36=36,2×18=36,3×12=36,4×9=36,6×6=36;
即和的乘积一定,所以和成反比例关系。
由题意得=36,
当=2.5时,2.5=36,=14.4
当=时,=36,y=108
【点睛】
此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
5. 16 15
【解析】
【分析】
已知x和y是成正比例的两个量,即x和y的比值一定,根据0.8和1.2成正比例,0.8∶1.2=2∶3,依据图示和x与y成正比例可列比例式:
x∶24=2∶3
x∶=2∶3
0.5∶y=2∶3
10∶y=2∶3
先根据比例基本性质:两内项之积等于两外项之积,化简方程,再解比例即可求解。
【详解】
x∶24=2∶3
3x=48
x=16
x∶=2∶3
3x=
x=
0.5∶y=2∶3
2y=1.5
y=
10∶y=2∶3
2y=30
y=15
【点睛】
本题主要考查学生对正比例意义的理解,以及列比例方程和解比例的能力。
6. 正 4 750
【解析】
【分析】
(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。题目中路程÷时间=速度,通过读图和计算,判断速度是否一定即可。
(2)由图可直接得到快车追上慢车的时间。
(3)求出的慢车的速度,从图中又知道了慢车走完全程用的时间,因此,可以得出A、B两地的路程。
【详解】
(1)100÷2=50(千米/时),300÷6=50(千米/时),结合图可知,慢车在匀速行驶,即速度是一定的,路程÷时间=速度(一定),所以慢车所行的路程和时间成正比例。
(2)快车从慢车出发后2小时出发,6小时的时候追上慢车,用了6-2=4小时追上慢车。
(3)由第(1)知道慢车的速度为50千米/时,慢车行驶完全程用了15小时,则A、B两地的路程是:50×15=750千米
【点睛】
本题考查了学生识图、读图、从图中获取信息的能力,通过图中信息计算出慢车的速度是解答本题的关键。
7.单价
【解析】
【分析】
总价一定,练习本的本数×单价=总价,乘积一定,根据反比例的意义,即可解答。
【详解】
总价一定,购买的练习本书和单价成反比例。
【点睛】
本题考查反比例的意义,根据反比例的意义解答。
8.650
【解析】
【详解】
略
9.√
【解析】
【详解】
略
10.√
【解析】
【分析】
圆的半径和周长是相关联的变量,半径越大,周长就越大,圆的周长除以半径,得到的结果是2π,是一个定值,符合正比例关系的要求。
【详解】
圆的半径和周长成正比例关系,题干阐述正确,答案为:√。
【点睛】
正比例关系必须满足三点基本要求,首先必须是两个相关联的变量,其次必须满足同增同减的变化规律,另外还要保证比值一定。
11.√
【解析】
【分析】
判断分母与分数值是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例.
【详解】
根据分数与除法的关系,知道分子相当于被除数,分母相当于除数,分数值相当于商,故被除数=商×除数,得出分数值×分母=分子(一定),
所以,分子一定,分母和分数值成反比例;
12.×
【解析】
【分析】
圆周长=直径×π,两个相关联的量,一种量变化,另一种量也随着变化,这两个量才可能成比例,在圆周长一定的情况下,直径与π这两个量中的π本身就是定值,那么直径也就是定值,这两个量不可能一个变,另一个也变。所以这两个量根本不成反比例。
【详解】
根据分析可知,圆周长一定,直径和π不成反比例。
所以原题说法错误。
【点睛】
此题主要考查学生对反比例判定的认识与理解。
13.√
【解析】
略
14.C
【解析】
判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例;如果不是比值或乘积一定,就不成比例.
【详解】
A、x+y=6,是和一定,不成比例;
B、x-y=8,是差一定,不成比例;
C、因为y=5x,y÷x=5,是比值一定,所以成正比例;
D、xy=7,是乘积一定,所以成反比例;
故答案为:C.
【点睛】
此题属于根据正、反比例的意义,判断两种相关联的量是成正比例还是成反比例,就看两种量是对应的比值一定,还是对应的乘积一定,再做出解答.
15.C
【解析】
【分析】
成正比例关系的两个量的比值一定,变化方向相同,据此解答。
【详解】
根据正比例的意义,图象①③中,甲和乙的变化方向相同,图象是一条射线,则甲和乙成正比例关系;图象②中,甲和乙的变化方向相反,则甲和乙不成正比例关系;图象④中,甲和乙的比值不一定,则甲和乙不成正比例关系。
故答案为:C
【点睛】
本题考查正比例的图象,根据正比例的意义即可解答。
16.C
【解析】
【分析】
成反比例的量:两种相关联的量,若一种量变化,另一种也随着变化,如果这两种中相对应的两个数的积一定,这两种量就叫做成反比例的量。它们的关系叫做反比例关系。字母关系为:x×y=k(一定);可结合实际分别列出每个选项中的数量关系式,并依据反比例的意义做出判断。
【详解】
结合反比例的意义及相关联的量之间的关系可得:
A.车轮的周长×车轮转动的圈数=行驶的路程(一定),所以,车轮的周长与车轮需要转动的圈数成反比例;
B.底×高=三角形的面积×2(一定),所以,三角形的底和高成反比例;
C.已走的路程+剩下的路程=从家到学校的路程(一定),所以,已走的路程和剩下的路程不成反比例;
D.平均速度×时间=从家到学校的路程(一定),所以,小东从家步行到学校的平均速度与所花的时间成反比例。
故答案为:C。
【点睛】
明确反比例的判断标准,即两种相关联的量的乘积一定;同时,对于相关联的量的数量关系,要能够熟练、准确把握。
17.C
【解析】
已知a与b成正比例,那么 a与b的比值一定,通过比例的基本性质:两个内项之积等于两个外项之积,即可解答。
【详解】
a∶b=1.5∶0.15=10∶1
2.5∶b=10∶1
10b=2.5
b=2.5÷10
b=0.25
故答案为:C
【点睛】
此题关键在于理解当两数成正比例后,不管它们代入何数,它们的比值是固定不变的。
18.C
【解析】
由于长方形A与长方形B等长,长方形B与长方形C等宽,设阴影所在的长方形的面积为x平方厘米,即可列比例求出这个长方形的面积,阴影部分占这个长方形面积的一半,由此即可求出阴影部分面积。
【详解】
解:设阴影所在的长方形的面积为x平方厘米。
2:x=4:5
4x=10
x=2.5
2.5÷2=(平方厘米)
答:阴影部分面积是厘米。
故选:C。
【点睛】
关键是求出阴影部分所在的长方形的面积。也可这样理解,长方形A与长方形B等长,长方形B与长方形C等宽,由于长方形A的面积是长方形B的一半,因此阴影部分所在的长方形的面积是长方形C的一半,从而求出阴影所在的长方形的面积,进而求出阴影部分面积。
19.(1)成正比例;工作总量工作时间工作效率(一定)
(2)成正比例;圆的直径周长(一定)
(3)成正比例;图上距离实际距离比例尺(一定)
(4)不成正比例;被减数差减数(一定),不是比值一定
【解析】
【分析】
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,据此解答。
【详解】
(1)因为工作总量工作时间工作效率(一定),符合正比例的意义,所以工作效率一定,工作总量与工作时间成正比例。
(2)圆的直径周长(一定),符合正比例的意义,所以圆的周长和直径成正比例。
(3)图上距离实际距离比例尺(一定),符合正比例的意义,所以图上距离和实际距离成正比例。
(4)被减数差减数(一定),不是比值一定,所以被减数和差不成正比例。
【点睛】
判断两个相关联的量之间是否成正比例,就看这两个量对应的比值,如果是比值一定,就成正比例。
20.正,2.5x,20,3.2.
【解析】
【详解】
试题分析:(1)根据表中的数据可知,5:2=7.5:3=10:4=12.5:6=15:6…=2.5,说明这些长方形的长与宽的比值一定,所以这些长方形的宽与长成正比例;再根据题意,用y表示长,x表示宽,则y=2.5x;
(2)根据y=2.5x,列式求得若长方形的宽是8厘米,长的厘米数;若长是8厘米,宽的厘米数;
(3)因为长方形的周长=(长+宽)×2,可设宽为x厘米,则长为2.5x厘米,列并解方程求得长和宽即可.
解:(1)因为5:2=7.5:3=10:4=12.5:6=15:6…=2.5(一定),
是对应的比值一定,所以这些长方形的宽与长成正比例,
如果用y表示长,x表示宽,则y=2.5x;
(2)当宽是8厘米,长是:2.5×8=20(厘米),
当长是8厘米,宽是:8÷2.5=3.2(厘米);
(3)宽为x厘米,则长为2.5x厘米,由题意得,
(x+2.5x)×2=70,
3.5x=35,
x=10,
长是:2.5×10=25(厘米);
答:它的长是25厘米,宽是10厘米.
点评:解决此题关键是先根据表中的数据辨识这些长方形的长与宽成什么比例,再根据长与宽的关系进一步解决其它的问题.
21.(1)360;450;540
(2)见详解
(3)成正比例
【解析】
【分析】
(1)根据速度×时间=路程,代入数据计算并填表即可;
(2)观察统计表数据,发现随着时间的增加路程也在增加,速度是一定的,时间与路程的比值也一定;据此解答。
(3)根据正比例的意义进行判定即可。
【详解】
(1)90÷1=90(千米/时)
180÷2=90(千米/时)
270÷3=90(千米/时)
即速度是90千米/时
所以4小时行驶:4×90=360(千米/时)
5小时行驶:5×90=450(千米/时)
6小时行驶:6×90=540(千米/时)
填表如下:
时间/时 1 2 3 4 5 6
路程/km 90 180 270 360 450 540
(2)由分析可知:路程随时间的变化而变化;路程与时间的比值一定。
(3)由于路程与时间的比值一定,所以路程与时间成正比例。
【点睛】
本题主要考查正比例的意义与辨识。
22.
长度/米 1 2 3 4 5
总价/元 60 120 180 240 300
成正比例关系;150元.
【解析】
【详解】
试题分析:(1)根据每米售价为60元,可知:买2米,需要2个60元即120元;买3米,需要3个60元即180元;买4米,需要4个60元即240元;买5米,需要5个60元即300元;
(2)在图中描出长度和总价对应的点,进而把这些点按顺序连起来即可;
(3)图象是一条经过原点的直线,观察图象可知,购买布匹需要的钱数随着长度的变化而变化,且变化方向相同,所以购买布匹的长度和需要的钱数成正比例关系;
(4)根据图象直接判断购买2.5米布匹需要的钱数即可.
解:(3)图象是一条经过原点的直线,可知购买布匹的长度和需要的钱数成正比例关系;
(4)根据图象可判断购买2.5米布匹需要150元.
答:购买2.5米布匹需要150元.
点评:此题考查正、反比例的应用,正比例关系的图象就是一条经过原点的直线.
试卷第页,共页
试卷第页,共页
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 总分
得分
一、填空题(共36分)
1.(本题2分)圆的周长一定,圆周率和它的直径( )。(在括号里填“成正比例”“成反比例”或“不成比例”)。
2.(本题2分)如果x∶4=5∶y,那么x和y成________比例。
3.(本题6分)在平行四边形里,底一定,面积和高 比例
高一定,面积和底 比例
面积一定,底和高 比例.
4.(本题6分)用x、y表示长方形相邻两边的长,下表是面积为36cm2的长方形相邻两边长度的变化关系。请把表格填完整,再填空。
x 1 2 3 4 6
y 36 ( ) 12 ( ) ( )
①x与y成( )比例。
②当x=2.5时,y=( )时,当x=时,y=( )。
5.(本题8分)已知x和y是成正比例的两个量,请把下表填写完整。
x 0.8 0.5 10
y 1.2 24
6.(本题6分)慢车和快车沿相同的路线从地到地所行路程和时间的关系如图所示:
(1)慢车行驶时间和路程成( )比例关系。
(2)快车追上慢车所需时间是( )小时。
(3)、两地之间的路程是( )千米。
7.(本题3分)总价一定,购买的练习本的本数和( )成反比例。
8.(本题3分)一个油厂用200千克黄豆可榨26千克油,照这样计算,5吨黄豆可榨油( )千克.
二、判断题(共12分)
9.(本题2分)同一时间、同一地点,物体的影长与物体的高度成正比例关系.( )
10.(本题2分)圆的半径和周长成正比例关系。( )
11.(本题2分)分子一定,分母和分数值成反比例.( )
12.(本题2分)圆周长一定,直径和π成反比例。( )
13.(本题2分)在,如果V一定,则S与h成反比例。( )
三、选择题(共10分)
14.(本题2分)表示x和y成正比例关系的式子是( )
A.x+y=6 B.x﹣y=8 C.y=5x D.xy=7
15.(本题2分)下面图象中,表示甲、乙两个量成正比例关系的有( )。
A.①② B.③④ C.①③ D.②④
16.(本题2分)下面各选项中的两个量不成反比例的是( )。
A.行驶的路程一定,车轮的周长与车轮需要转动的圈数。 B.三角形的面积一定,它的底和高。
C.小东从家步行到学校,已走的路程和剩下的路程。 D.小东从家步行到学校的平均速度与所花的时间。
17.(本题2分)a与b成正比例,并且当a=1.5时,b=0.15,那么当a=2.5时,b=( )。
A.25 B.2.5 C.0.25
18.(本题2分)如下图所示,一个大长方形被两条线段分成四个小长方形。如果其中图形A、B、C的面积分别是2cm2、4cm2和5cm2那么阴影部分的面积为( )cm2。
A.1 B. C. D.
四、解答题(共42分)
19.(本题12分)判断下面各题中的两种量是否成正比例,并说明理由。
(1)工作效率一定,工作时间和工作总量。
(2)圆的周长和直径。
(3)比例尺一定,图上距离和实际距离。
(4)减数一定,被减数和差。
20.(本题9分)一些长方形的长与宽的长度变化如表.
长/厘米 5 7.5 10 12.5 15 17.5 …
宽/厘米 2 3 4 5 6 7 …
(1)这些长方形的宽与长成 比例.如果用y表示长,x表示宽,则y= .
(2)若长方形的宽是8厘米,长是 厘米:若长是8厘米,宽是 厘米.
(3)这样的长方形中,当周长是70厘米时,它的长和宽各是多少?(列式解答)
21.(本题9分)一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。
时间/时 1 2 3 4 5 6
路程/km 90 180 270
(1)把下表填写完整。
(2)你发现了什么?
(3)路程与时间成正比例吗?
22.(本题12分)一种服装布料每米售价为60元,购买2米、3米、…各需要多少元?
(1)填写下表.
长度/米 1 2 3 4 5
总价/元 60
(2)根据表中的数据,在如图中描出长度和总价对应的点,把这些点按顺序连起来.
(3)购买布匹的长度和需要的钱数有什么关系?
(4)根据图象判断,购买2.5米布匹需要多少钱?
试卷第页,共页
试卷第页,共页
参考答案:
1.不成比例
【解析】
【分析】
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】
因为圆周率是一个固定不变的数,不能随着圆的直径的变化而变化,所以圆周率和圆的直径不成比例。
【点睛】
此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
2.反
【解析】
【分析】
根据比例的基本性质,外项积等于内项积,得到xy=4×5,x和y的乘积为定值,典型的反比例关系。
【详解】
xy=4×5=20
所以x和y成反比例。
【点睛】
满足反比例关系的两个量,必须满足乘积一定的基本条件,可以利用一般表达式xy=k来判断。
3.正,正,反.
【解析】
【详解】
试题分析:判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
解:因为平行四边形的面积÷高=底(一定),所以面积和高正比例;
因为平行四边形的面积÷底=高(一定),所以面积和底正比例;
因为平行四边形的底×高=面积(一定),所以底和高反比例;
点评:此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
4. 18 9 6 反 14.4 108
【解析】
【分析】
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】
(1)因为1×36=36,2×18=36,3×12=36,4×9=36,6×6=36;
即和的乘积一定,所以和成反比例关系。
由题意得=36,
当=2.5时,2.5=36,=14.4
当=时,=36,y=108
【点睛】
此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
5. 16 15
【解析】
【分析】
已知x和y是成正比例的两个量,即x和y的比值一定,根据0.8和1.2成正比例,0.8∶1.2=2∶3,依据图示和x与y成正比例可列比例式:
x∶24=2∶3
x∶=2∶3
0.5∶y=2∶3
10∶y=2∶3
先根据比例基本性质:两内项之积等于两外项之积,化简方程,再解比例即可求解。
【详解】
x∶24=2∶3
3x=48
x=16
x∶=2∶3
3x=
x=
0.5∶y=2∶3
2y=1.5
y=
10∶y=2∶3
2y=30
y=15
【点睛】
本题主要考查学生对正比例意义的理解,以及列比例方程和解比例的能力。
6. 正 4 750
【解析】
【分析】
(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。题目中路程÷时间=速度,通过读图和计算,判断速度是否一定即可。
(2)由图可直接得到快车追上慢车的时间。
(3)求出的慢车的速度,从图中又知道了慢车走完全程用的时间,因此,可以得出A、B两地的路程。
【详解】
(1)100÷2=50(千米/时),300÷6=50(千米/时),结合图可知,慢车在匀速行驶,即速度是一定的,路程÷时间=速度(一定),所以慢车所行的路程和时间成正比例。
(2)快车从慢车出发后2小时出发,6小时的时候追上慢车,用了6-2=4小时追上慢车。
(3)由第(1)知道慢车的速度为50千米/时,慢车行驶完全程用了15小时,则A、B两地的路程是:50×15=750千米
【点睛】
本题考查了学生识图、读图、从图中获取信息的能力,通过图中信息计算出慢车的速度是解答本题的关键。
7.单价
【解析】
【分析】
总价一定,练习本的本数×单价=总价,乘积一定,根据反比例的意义,即可解答。
【详解】
总价一定,购买的练习本书和单价成反比例。
【点睛】
本题考查反比例的意义,根据反比例的意义解答。
8.650
【解析】
【详解】
略
9.√
【解析】
【详解】
略
10.√
【解析】
【分析】
圆的半径和周长是相关联的变量,半径越大,周长就越大,圆的周长除以半径,得到的结果是2π,是一个定值,符合正比例关系的要求。
【详解】
圆的半径和周长成正比例关系,题干阐述正确,答案为:√。
【点睛】
正比例关系必须满足三点基本要求,首先必须是两个相关联的变量,其次必须满足同增同减的变化规律,另外还要保证比值一定。
11.√
【解析】
【分析】
判断分母与分数值是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例.
【详解】
根据分数与除法的关系,知道分子相当于被除数,分母相当于除数,分数值相当于商,故被除数=商×除数,得出分数值×分母=分子(一定),
所以,分子一定,分母和分数值成反比例;
12.×
【解析】
【分析】
圆周长=直径×π,两个相关联的量,一种量变化,另一种量也随着变化,这两个量才可能成比例,在圆周长一定的情况下,直径与π这两个量中的π本身就是定值,那么直径也就是定值,这两个量不可能一个变,另一个也变。所以这两个量根本不成反比例。
【详解】
根据分析可知,圆周长一定,直径和π不成反比例。
所以原题说法错误。
【点睛】
此题主要考查学生对反比例判定的认识与理解。
13.√
【解析】
略
14.C
【解析】
判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例;如果不是比值或乘积一定,就不成比例.
【详解】
A、x+y=6,是和一定,不成比例;
B、x-y=8,是差一定,不成比例;
C、因为y=5x,y÷x=5,是比值一定,所以成正比例;
D、xy=7,是乘积一定,所以成反比例;
故答案为:C.
【点睛】
此题属于根据正、反比例的意义,判断两种相关联的量是成正比例还是成反比例,就看两种量是对应的比值一定,还是对应的乘积一定,再做出解答.
15.C
【解析】
【分析】
成正比例关系的两个量的比值一定,变化方向相同,据此解答。
【详解】
根据正比例的意义,图象①③中,甲和乙的变化方向相同,图象是一条射线,则甲和乙成正比例关系;图象②中,甲和乙的变化方向相反,则甲和乙不成正比例关系;图象④中,甲和乙的比值不一定,则甲和乙不成正比例关系。
故答案为:C
【点睛】
本题考查正比例的图象,根据正比例的意义即可解答。
16.C
【解析】
【分析】
成反比例的量:两种相关联的量,若一种量变化,另一种也随着变化,如果这两种中相对应的两个数的积一定,这两种量就叫做成反比例的量。它们的关系叫做反比例关系。字母关系为:x×y=k(一定);可结合实际分别列出每个选项中的数量关系式,并依据反比例的意义做出判断。
【详解】
结合反比例的意义及相关联的量之间的关系可得:
A.车轮的周长×车轮转动的圈数=行驶的路程(一定),所以,车轮的周长与车轮需要转动的圈数成反比例;
B.底×高=三角形的面积×2(一定),所以,三角形的底和高成反比例;
C.已走的路程+剩下的路程=从家到学校的路程(一定),所以,已走的路程和剩下的路程不成反比例;
D.平均速度×时间=从家到学校的路程(一定),所以,小东从家步行到学校的平均速度与所花的时间成反比例。
故答案为:C。
【点睛】
明确反比例的判断标准,即两种相关联的量的乘积一定;同时,对于相关联的量的数量关系,要能够熟练、准确把握。
17.C
【解析】
已知a与b成正比例,那么 a与b的比值一定,通过比例的基本性质:两个内项之积等于两个外项之积,即可解答。
【详解】
a∶b=1.5∶0.15=10∶1
2.5∶b=10∶1
10b=2.5
b=2.5÷10
b=0.25
故答案为:C
【点睛】
此题关键在于理解当两数成正比例后,不管它们代入何数,它们的比值是固定不变的。
18.C
【解析】
由于长方形A与长方形B等长,长方形B与长方形C等宽,设阴影所在的长方形的面积为x平方厘米,即可列比例求出这个长方形的面积,阴影部分占这个长方形面积的一半,由此即可求出阴影部分面积。
【详解】
解:设阴影所在的长方形的面积为x平方厘米。
2:x=4:5
4x=10
x=2.5
2.5÷2=(平方厘米)
答:阴影部分面积是厘米。
故选:C。
【点睛】
关键是求出阴影部分所在的长方形的面积。也可这样理解,长方形A与长方形B等长,长方形B与长方形C等宽,由于长方形A的面积是长方形B的一半,因此阴影部分所在的长方形的面积是长方形C的一半,从而求出阴影所在的长方形的面积,进而求出阴影部分面积。
19.(1)成正比例;工作总量工作时间工作效率(一定)
(2)成正比例;圆的直径周长(一定)
(3)成正比例;图上距离实际距离比例尺(一定)
(4)不成正比例;被减数差减数(一定),不是比值一定
【解析】
【分析】
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,据此解答。
【详解】
(1)因为工作总量工作时间工作效率(一定),符合正比例的意义,所以工作效率一定,工作总量与工作时间成正比例。
(2)圆的直径周长(一定),符合正比例的意义,所以圆的周长和直径成正比例。
(3)图上距离实际距离比例尺(一定),符合正比例的意义,所以图上距离和实际距离成正比例。
(4)被减数差减数(一定),不是比值一定,所以被减数和差不成正比例。
【点睛】
判断两个相关联的量之间是否成正比例,就看这两个量对应的比值,如果是比值一定,就成正比例。
20.正,2.5x,20,3.2.
【解析】
【详解】
试题分析:(1)根据表中的数据可知,5:2=7.5:3=10:4=12.5:6=15:6…=2.5,说明这些长方形的长与宽的比值一定,所以这些长方形的宽与长成正比例;再根据题意,用y表示长,x表示宽,则y=2.5x;
(2)根据y=2.5x,列式求得若长方形的宽是8厘米,长的厘米数;若长是8厘米,宽的厘米数;
(3)因为长方形的周长=(长+宽)×2,可设宽为x厘米,则长为2.5x厘米,列并解方程求得长和宽即可.
解:(1)因为5:2=7.5:3=10:4=12.5:6=15:6…=2.5(一定),
是对应的比值一定,所以这些长方形的宽与长成正比例,
如果用y表示长,x表示宽,则y=2.5x;
(2)当宽是8厘米,长是:2.5×8=20(厘米),
当长是8厘米,宽是:8÷2.5=3.2(厘米);
(3)宽为x厘米,则长为2.5x厘米,由题意得,
(x+2.5x)×2=70,
3.5x=35,
x=10,
长是:2.5×10=25(厘米);
答:它的长是25厘米,宽是10厘米.
点评:解决此题关键是先根据表中的数据辨识这些长方形的长与宽成什么比例,再根据长与宽的关系进一步解决其它的问题.
21.(1)360;450;540
(2)见详解
(3)成正比例
【解析】
【分析】
(1)根据速度×时间=路程,代入数据计算并填表即可;
(2)观察统计表数据,发现随着时间的增加路程也在增加,速度是一定的,时间与路程的比值也一定;据此解答。
(3)根据正比例的意义进行判定即可。
【详解】
(1)90÷1=90(千米/时)
180÷2=90(千米/时)
270÷3=90(千米/时)
即速度是90千米/时
所以4小时行驶:4×90=360(千米/时)
5小时行驶:5×90=450(千米/时)
6小时行驶:6×90=540(千米/时)
填表如下:
时间/时 1 2 3 4 5 6
路程/km 90 180 270 360 450 540
(2)由分析可知:路程随时间的变化而变化;路程与时间的比值一定。
(3)由于路程与时间的比值一定,所以路程与时间成正比例。
【点睛】
本题主要考查正比例的意义与辨识。
22.
长度/米 1 2 3 4 5
总价/元 60 120 180 240 300
成正比例关系;150元.
【解析】
【详解】
试题分析:(1)根据每米售价为60元,可知:买2米,需要2个60元即120元;买3米,需要3个60元即180元;买4米,需要4个60元即240元;买5米,需要5个60元即300元;
(2)在图中描出长度和总价对应的点,进而把这些点按顺序连起来即可;
(3)图象是一条经过原点的直线,观察图象可知,购买布匹需要的钱数随着长度的变化而变化,且变化方向相同,所以购买布匹的长度和需要的钱数成正比例关系;
(4)根据图象直接判断购买2.5米布匹需要的钱数即可.
解:(3)图象是一条经过原点的直线,可知购买布匹的长度和需要的钱数成正比例关系;
(4)根据图象可判断购买2.5米布匹需要150元.
答:购买2.5米布匹需要150元.
点评:此题考查正、反比例的应用,正比例关系的图象就是一条经过原点的直线.
试卷第页,共页
试卷第页,共页
