2021-2022学年人教版八年级数学下册18.1.1平行四边形的性质同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.1.1平行四边形的性质同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 234.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 15:21:47 | ||
图片预览



文档简介
2021——2022学年度人教版八年级数学下册 第十八章 平行四边形
18.1.1 平行四边形的性质同步练习
一、选择题
1.下列性质中,平行四边形不具有的是( )
A.对角线相等 B.对角线互相平分
C.相邻两角互补 D.两组对边分别相等
2.有下列说法:
①平行四边形具有四边形的所有性质:②平行四边形是中心对称图形:③平行四边形的任一条对角线可把平行四边形分成两个全等的三角形;④平行四边形的两条对角线把平行四边形分成4个面积相等的小三角形.
其中正确说法的序号是( ).A.①②④ B.①③④ C.①②③ D.①②③④
3.如图,平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则EC等于( )
A.1 B.2 C.3 D.4
4.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上,若∠DCE=128°,则∠A=( )
A.32° B.42° C.52° D.62°
5.如图,在平行四边形ABCD中,∠A+∠C=130°,则∠B的度数为( )
A.130° B.115° C.105° D.95°
6.如图,在中,的平分线交于点,的平分线交于点,若,,则的长是( )
A.4 B.5 C.7 D.6
7.如图,在中,,为对角线,将沿方向平移,使得与重合,点的对应点为点,过点作交的延长线于点,则下列说法正确的是( )
A. B.平分 C. D.
8.如图,在平行四边形中,对角线,相交于点,下列条说法不正确的是( )
A. B.
C. D.
9.如图, ABCD的对角线AC,BD相交于点O,则下列结论一定正确的是( )
A.OB=OD B.AB=BC C.AC⊥BD D.∠ABD=∠CBD
10.如图,在 Rt△ABC 中,∠ACB=90°,CD⊥AB,D为垂足. E是AB边上的一个动点,以CE,BE为邻边画平行四边形CEBF,则下列线段的长等于对角线EF最小值的是( ).
A.AC B.BC C.CD D.AB
二、填空题
11.在平行四边形ABCD中,对角线AC长为8cm,,,则它的面积为______cm2.
12.如图,平行四边形ABCD中,AE平分∠BAD,若CE=4cm,AD=5cm,则平行四边形ABCD的周长是___cm.
13.如图,直线过的中心点,交于点,交于点,己知,则S阴影=______.
14.如图,平行四边形ABCD中,,,与的平分线分别交AB于F、E,则____________
15.如图, ABCD中,AB=3,BC=5,AE平分∠BAD交BC于点E,则CE的长为________ .
三、解答题
16. ABCD的对角线AC,BD交于点O,AB⊥BD,若AB=4,AC=10,.求BD的长.
17.如图,在平行四边形中,已知对角线与相交于点O,,,,求的长.
18.已知平行四边形ABCD,AB=8cm,BC=10cm,,求平行四边形ABCD的面积.
19.如图,在中,是的中点,的延长线与的延长线相交于点.求证:.
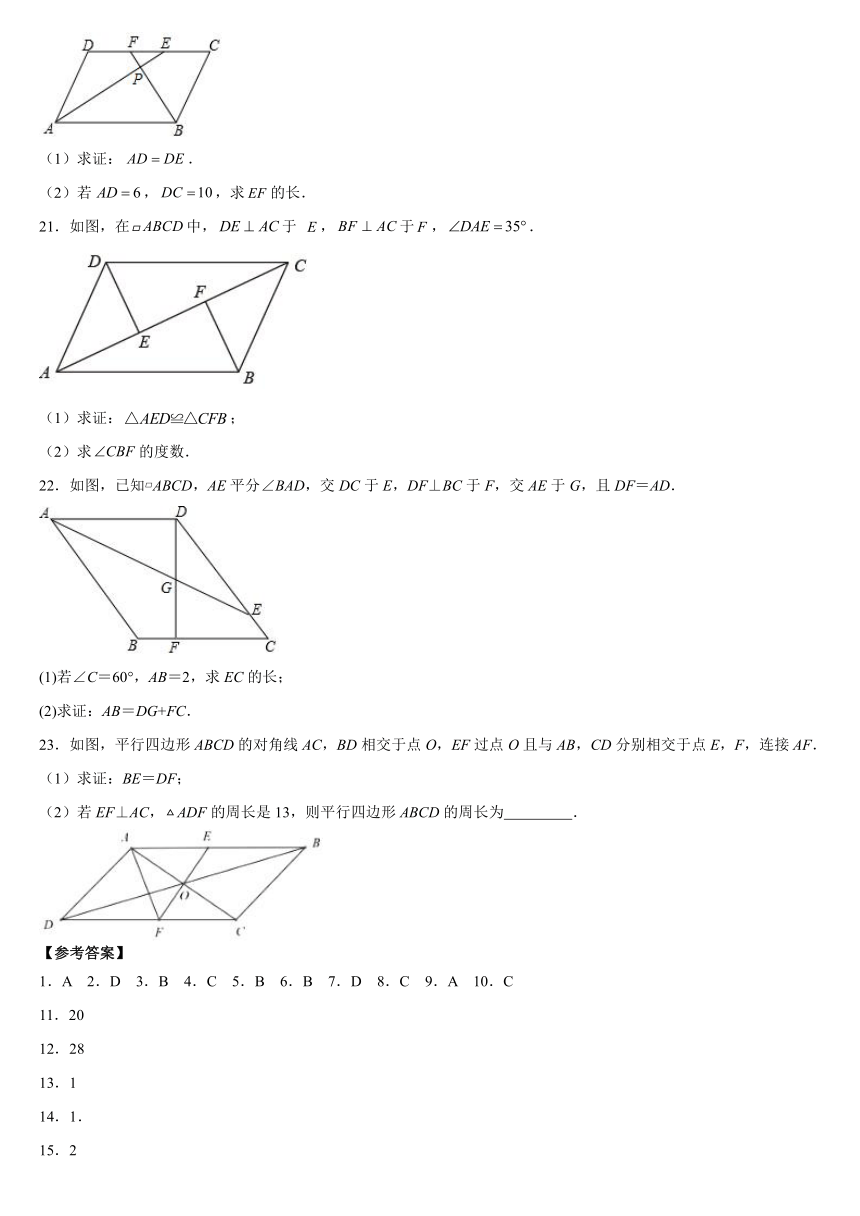
20.如图,四边形是平行四边形,和分别平分和,交于,.与相交于点,
(1)求证:.
(2)若,,求的长.
21.如图,在中,于 ,于,.
(1)求证:;
(2)求的度数.
22.如图,已知 ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.
(1)若∠C=60°,AB=2,求EC的长;
(2)求证:AB=DG+FC.
23.如图,平行四边形ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F,连接AF.
(1)求证:BE=DF;
(2)若EF⊥AC,ADF的周长是13,则平行四边形ABCD的周长为 .
【参考答案】
1.A 2.D 3.B 4.C 5.B 6.B 7.D 8.C 9.A 10.C
11.20
12.28
13.1
14.1.
15.2
16.解:∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO.
∵AC=10,
∴AO=5.
∵AB⊥BD,AB=4,
∴BO=.
∴BD=2BO=6.
17.解:∵四边形ABCD是平行四边形,
∴OB=OD,AD∥BC,
∵∠DBC=90°,
∴∠ADB=90°,
在Rt△ADB中,
∵AB=10,AD=6,
∴BD==8,
∴OD=BD=4.
18.解:过点A作AE⊥BC于点E,如图所示:
∴,
∵,AB=8cm,
∴cm,
∵BC=10cm,
∴.
19.解:∵四边形为平行四边形,
∵,
∴,AD=BC
∵是的中点,
∴,
在和中,
∵,
∴≌(ASA),
∴,
又∵,
∴.
20.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∴∠DAE=∠DEA,
∴AD=DE;
(2)∵AD=6,DC=10,
∴DE=AD=6,
∴EC=DC-DE=10-6=4,
∵四边形ABCD是平行四边形,
∴AB∥DC,AD=BC=6,
∴∠CFB=∠FBA,
∵BF平分∠CBA,
∴∠CBF=∠FBA,
∴∠CFB=∠CBF,
∴BC=FC=6,
∴EF=FC-EC=6-4=2.
21.(1)证明:在平行四边形中,,
又,
,
,.
,
在和中,
(2)解:在中,, ,
.
22.(1)解:在中,,,,
∴,
∴,
在中,
,
.
,
∵,平分,
,,
,
;
(2)证明:如图所示:延长至,连接,使,
在和中,
,
,,
由(1)可得:
,
,即,
,
即.
23.(1)证明:∵四边形是平行四边形,
∴,,
∴,
在与中,
,
∴,
∴;
(2),,
,
的周长为,
平行四边形的周长为.
故答案为:26.
18.1.1 平行四边形的性质同步练习
一、选择题
1.下列性质中,平行四边形不具有的是( )
A.对角线相等 B.对角线互相平分
C.相邻两角互补 D.两组对边分别相等
2.有下列说法:
①平行四边形具有四边形的所有性质:②平行四边形是中心对称图形:③平行四边形的任一条对角线可把平行四边形分成两个全等的三角形;④平行四边形的两条对角线把平行四边形分成4个面积相等的小三角形.
其中正确说法的序号是( ).A.①②④ B.①③④ C.①②③ D.①②③④
3.如图,平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则EC等于( )
A.1 B.2 C.3 D.4
4.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上,若∠DCE=128°,则∠A=( )
A.32° B.42° C.52° D.62°
5.如图,在平行四边形ABCD中,∠A+∠C=130°,则∠B的度数为( )
A.130° B.115° C.105° D.95°
6.如图,在中,的平分线交于点,的平分线交于点,若,,则的长是( )
A.4 B.5 C.7 D.6
7.如图,在中,,为对角线,将沿方向平移,使得与重合,点的对应点为点,过点作交的延长线于点,则下列说法正确的是( )
A. B.平分 C. D.
8.如图,在平行四边形中,对角线,相交于点,下列条说法不正确的是( )
A. B.
C. D.
9.如图, ABCD的对角线AC,BD相交于点O,则下列结论一定正确的是( )
A.OB=OD B.AB=BC C.AC⊥BD D.∠ABD=∠CBD
10.如图,在 Rt△ABC 中,∠ACB=90°,CD⊥AB,D为垂足. E是AB边上的一个动点,以CE,BE为邻边画平行四边形CEBF,则下列线段的长等于对角线EF最小值的是( ).
A.AC B.BC C.CD D.AB
二、填空题
11.在平行四边形ABCD中,对角线AC长为8cm,,,则它的面积为______cm2.
12.如图,平行四边形ABCD中,AE平分∠BAD,若CE=4cm,AD=5cm,则平行四边形ABCD的周长是___cm.
13.如图,直线过的中心点,交于点,交于点,己知,则S阴影=______.
14.如图,平行四边形ABCD中,,,与的平分线分别交AB于F、E,则____________
15.如图, ABCD中,AB=3,BC=5,AE平分∠BAD交BC于点E,则CE的长为________ .
三、解答题
16. ABCD的对角线AC,BD交于点O,AB⊥BD,若AB=4,AC=10,.求BD的长.
17.如图,在平行四边形中,已知对角线与相交于点O,,,,求的长.
18.已知平行四边形ABCD,AB=8cm,BC=10cm,,求平行四边形ABCD的面积.
19.如图,在中,是的中点,的延长线与的延长线相交于点.求证:.
20.如图,四边形是平行四边形,和分别平分和,交于,.与相交于点,
(1)求证:.
(2)若,,求的长.
21.如图,在中,于 ,于,.
(1)求证:;
(2)求的度数.
22.如图,已知 ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.
(1)若∠C=60°,AB=2,求EC的长;
(2)求证:AB=DG+FC.
23.如图,平行四边形ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F,连接AF.
(1)求证:BE=DF;
(2)若EF⊥AC,ADF的周长是13,则平行四边形ABCD的周长为 .
【参考答案】
1.A 2.D 3.B 4.C 5.B 6.B 7.D 8.C 9.A 10.C
11.20
12.28
13.1
14.1.
15.2
16.解:∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO.
∵AC=10,
∴AO=5.
∵AB⊥BD,AB=4,
∴BO=.
∴BD=2BO=6.
17.解:∵四边形ABCD是平行四边形,
∴OB=OD,AD∥BC,
∵∠DBC=90°,
∴∠ADB=90°,
在Rt△ADB中,
∵AB=10,AD=6,
∴BD==8,
∴OD=BD=4.
18.解:过点A作AE⊥BC于点E,如图所示:
∴,
∵,AB=8cm,
∴cm,
∵BC=10cm,
∴.
19.解:∵四边形为平行四边形,
∵,
∴,AD=BC
∵是的中点,
∴,
在和中,
∵,
∴≌(ASA),
∴,
又∵,
∴.
20.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∴∠DAE=∠DEA,
∴AD=DE;
(2)∵AD=6,DC=10,
∴DE=AD=6,
∴EC=DC-DE=10-6=4,
∵四边形ABCD是平行四边形,
∴AB∥DC,AD=BC=6,
∴∠CFB=∠FBA,
∵BF平分∠CBA,
∴∠CBF=∠FBA,
∴∠CFB=∠CBF,
∴BC=FC=6,
∴EF=FC-EC=6-4=2.
21.(1)证明:在平行四边形中,,
又,
,
,.
,
在和中,
(2)解:在中,, ,
.
22.(1)解:在中,,,,
∴,
∴,
在中,
,
.
,
∵,平分,
,,
,
;
(2)证明:如图所示:延长至,连接,使,
在和中,
,
,,
由(1)可得:
,
,即,
,
即.
23.(1)证明:∵四边形是平行四边形,
∴,,
∴,
在与中,
,
∴,
∴;
(2),,
,
的周长为,
平行四边形的周长为.
故答案为:26.
