2021--2022学年人教版九年级数学下册27.1图形的相似同步练习(Word版含答案)
文档属性
| 名称 | 2021--2022学年人教版九年级数学下册27.1图形的相似同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 320.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 15:34:10 | ||
图片预览




文档简介
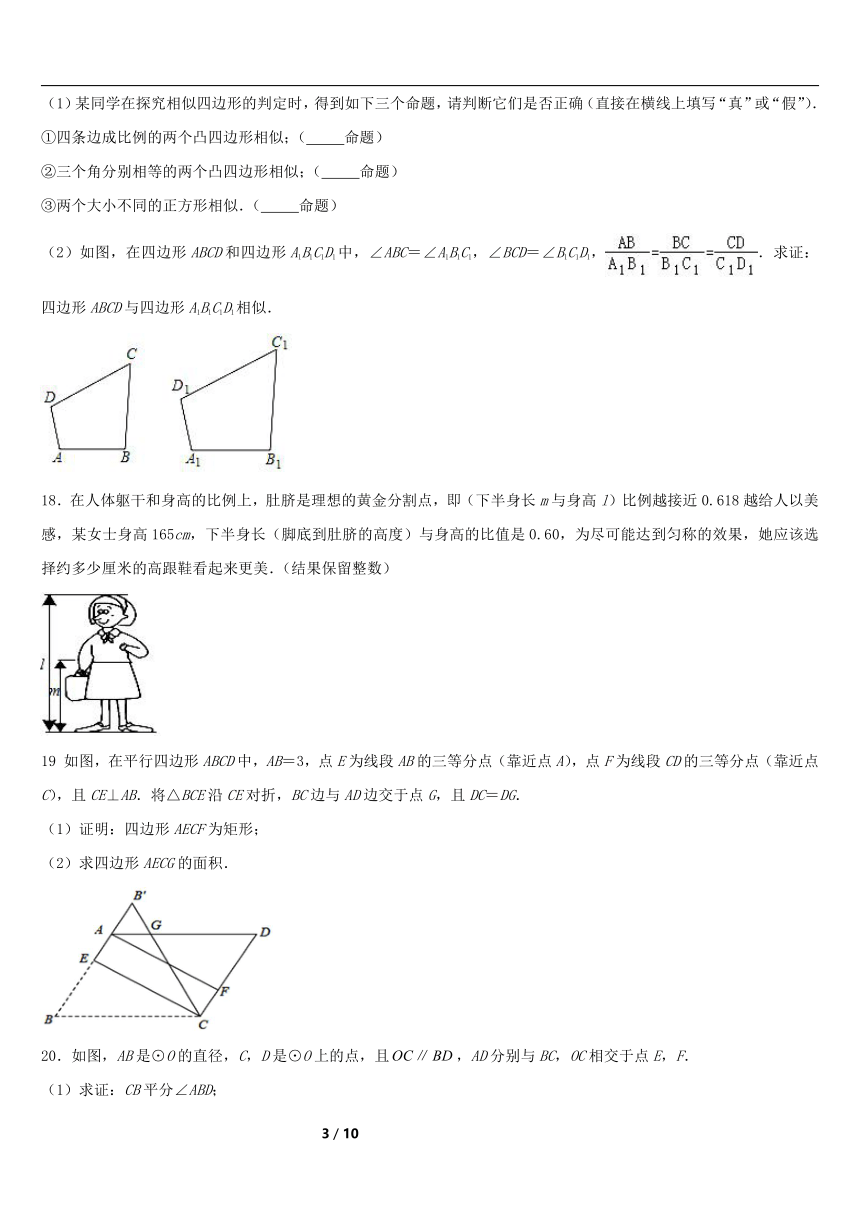
27.1 图形的相似----人教版九年级下册同步练习
一、单选题
1.在下面的图形中,相似的一组是( )
A. B.
C. D.
2.已知,那么下列等式中成立的是( )
A. B. C. D..
3.已知点 是线段 上的一点,线段是和的比例中项,下列结论中,正确的是( )
A. B. C. D.
4.点P是线段AB的黄金分割点,AP> BP,若BP=-1,AB的长为( )
A.+1 B.2 C.3+ D.3-
5.如图2中的矩形边长分别是将图1中的矩形边长4拉长2x,边长5拉长x得到的,若两个矩形相似(不全等),则x的值是( )
A.3 B.4 C.5 D.6
6.若矩形ABCD∽矩形EFGH,相似比为2:3,已知AB=4cm,BC=5cm,则矩形EFGH的周长是( )
A.12cm B.27cm C.24cm D.18cm
7.下面四组图形中,必是相似三角形的为( )
A.两个直角三角形
B.两条边对应成比例,一个对应角相等的两个三角形
C.有一个角为40°的两个等腰三角形
D.有一个角为100°的两个等腰三角形
8.若=,则的值是( )
A. B. C. D.
9.下列说法正确的是( )
A.所有菱形都相似 B.所有矩形都相似
C.所有正方形都相似 D.所有平行四边形都相似
二、填空题
10.以正方形各边的中点为顶点,可以组成一个新正方形,则新正方形与原正方形的相似比为 。
11.已知,那么(a﹣b):a=___.
12.已知线段AB=2cm,点P是AB的黄金分割点,且AP>PB,那么AP的长度是_______cm(结果保留根号)
13.如图,,,,,则__.
14.如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕EF与AC相交于点O,连接BO.若AB=4,CF=5,则OB的长为_______________.
三、解答题
15.如图,四边形 四边形 ,求边 、 的长度和角 的大小.
16.在一张比例尺为1:20的地图上,有一块多边形区域的周长是24cm,面积是20cm2,求这个区域的实际周长和面积.
17.根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形,相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
①四条边成比例的两个凸四边形相似;( 命题)
②三个角分别相等的两个凸四边形相似;( 命题)
③两个大小不同的正方形相似.( 命题)
(2)如图,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,.求证:四边形ABCD与四边形A1B1C1D1相似.
18.在人体躯干和身高的比例上,肚脐是理想的黄金分割点,即(下半身长m与身高l)比例越接近0.618越给人以美感,某女士身高165cm,下半身长(脚底到肚脐的高度)与身高的比值是0.60,为尽可能达到匀称的效果,她应该选择约多少厘米的高跟鞋看起来更美.(结果保留整数)
19 如图,在平行四边形ABCD中,AB=3,点E为线段AB的三等分点(靠近点A),点F为线段CD的三等分点(靠近点C),且CE⊥AB.将△BCE沿CE对折,BC边与AD边交于点G,且DC=DG.
(1)证明:四边形AECF为矩形;
(2)求四边形AECG的面积.
20.如图,AB是⊙O的直径,C,D是⊙O上的点,且,AD分别与BC,OC相交于点E,F.
(1)求证:CB平分∠ABD;
(2)若AB=8,AD=6,求CF的长.
答案解析部分
C 2.C 3.C 4.A 5.A 6.B 7.D 8.A 9.C
10答案为. :1
11答案为.1:3
12答案为.
13答案为.
14答案为.2
15.解:∵四边形 四边形 ,
∴ , , .
∴ , , .
16.这个区域的实际周长480cm,面积8000cm2.
17.根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形,相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
①四条边成比例的两个凸四边形相似;( 假 命题)
②三个角分别相等的两个凸四边形相似;( 假 命题)
③两个大小不同的正方形相似.( 真 命题)
(2)如图,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,.求证:四边形ABCD与四边形A1B1C1D1相似.
【解答】(1)解:①四条边成比例的两个凸四边形相似,是假命题,角不一定相等;
②三个角分别相等的两个凸四边形相似,是假命题,边不一定成比例;
③两个大小不同的正方形相似,是真命题;
故答案为:假,假,真;
(2)证明:如图,连接BD,B1D1.
∵∠BCD=∠B1C1D1,且,
∴△BCD∽△B1C1D1,
∴∠CDB=∠C1D1B1,∠C1B1D1=∠CBD,
∵,
∴,
∵∠ABC=∠A1B1C1,
∴∠ABD=∠A1B1D1,
∴△ABD∽△A1B1D1,
∴,
∴∠A=∠A1,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,
∴四边形ABCD与四边形A1B1C1D1相似.
18.在人体躯干和身高的比例上,肚脐是理想的黄金分割点,即(下半身长m与身高l)比例越接近0.618越给人以美感,某女士身高165cm,下半身长(脚底到肚脐的高度)与身高的比值是0.60,为尽可能达到匀称的效果,她应该选择约多少厘米的高跟鞋看起来更美.(结果保留整数)
【解答】解:根据已知条件可知:
下半身长是165×0.6=99(厘米),
设需要穿的高跟鞋为y厘米,则根据黄金分割定义,得
=0.618,
解得:y≈8,
经检验y≈8是原方程的根,
答:她应该选择大约8厘米的高跟鞋.
19.(1)证明:∵ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵点E为线段AB的三等分点(靠近点A),
∴AE=AB,
∵点F为线段CD的三等分点(靠近点C),
∴CF=CD,
∴AE=CF,
又∵AE∥CF,
∴四边形AECF为平行四边形,
∵CE⊥AB,
∴四边形AECF为矩形;
(2)∵AB=3,
∴AE=CF=1,BE=2,
∵将△BCE沿CE对折得到△ECB',
∴B'E=BE=2,
∴AB'=1,
∵DC=DG=3,
∴∠DGC=∠DCG,
∵BB'∥CD,
∴∠DCG=∠B',
∴∠B'=∠DGC,
∵∠DGC=∠B'GA,
∴∠B'=∠B'GA,
∴AB'=AG=1,
∴DA=BC=B'C=4,
∵AB'∥CD,
∴,
∴,
∴B'G=1,
∴△AGB'是等边三角形,
∴A B'=AG=B'G=1,
作GH⊥A B'于H,
则AH=A B'=,
∴GH=,
在Rt△BCE中,BC=4,BE=2,
∴EC==2,
∴S四边形AECG=S△EB'C-S△AB'G=.
20.(1)证明:∵
∴∠OCB=∠DBC,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OBC=∠DBC,
∴CB平分∠ABD;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
由勾股定理得:,
∵,AO=BO,
∴AF=DF,
∴,
∵直径AB=8,
∴OC=OB=4,
∴CF=OC﹣OF=
1 / 3
一、单选题
1.在下面的图形中,相似的一组是( )
A. B.
C. D.
2.已知,那么下列等式中成立的是( )
A. B. C. D..
3.已知点 是线段 上的一点,线段是和的比例中项,下列结论中,正确的是( )
A. B. C. D.
4.点P是线段AB的黄金分割点,AP> BP,若BP=-1,AB的长为( )
A.+1 B.2 C.3+ D.3-
5.如图2中的矩形边长分别是将图1中的矩形边长4拉长2x,边长5拉长x得到的,若两个矩形相似(不全等),则x的值是( )
A.3 B.4 C.5 D.6
6.若矩形ABCD∽矩形EFGH,相似比为2:3,已知AB=4cm,BC=5cm,则矩形EFGH的周长是( )
A.12cm B.27cm C.24cm D.18cm
7.下面四组图形中,必是相似三角形的为( )
A.两个直角三角形
B.两条边对应成比例,一个对应角相等的两个三角形
C.有一个角为40°的两个等腰三角形
D.有一个角为100°的两个等腰三角形
8.若=,则的值是( )
A. B. C. D.
9.下列说法正确的是( )
A.所有菱形都相似 B.所有矩形都相似
C.所有正方形都相似 D.所有平行四边形都相似
二、填空题
10.以正方形各边的中点为顶点,可以组成一个新正方形,则新正方形与原正方形的相似比为 。
11.已知,那么(a﹣b):a=___.
12.已知线段AB=2cm,点P是AB的黄金分割点,且AP>PB,那么AP的长度是_______cm(结果保留根号)
13.如图,,,,,则__.
14.如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕EF与AC相交于点O,连接BO.若AB=4,CF=5,则OB的长为_______________.
三、解答题
15.如图,四边形 四边形 ,求边 、 的长度和角 的大小.
16.在一张比例尺为1:20的地图上,有一块多边形区域的周长是24cm,面积是20cm2,求这个区域的实际周长和面积.
17.根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形,相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
①四条边成比例的两个凸四边形相似;( 命题)
②三个角分别相等的两个凸四边形相似;( 命题)
③两个大小不同的正方形相似.( 命题)
(2)如图,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,.求证:四边形ABCD与四边形A1B1C1D1相似.
18.在人体躯干和身高的比例上,肚脐是理想的黄金分割点,即(下半身长m与身高l)比例越接近0.618越给人以美感,某女士身高165cm,下半身长(脚底到肚脐的高度)与身高的比值是0.60,为尽可能达到匀称的效果,她应该选择约多少厘米的高跟鞋看起来更美.(结果保留整数)
19 如图,在平行四边形ABCD中,AB=3,点E为线段AB的三等分点(靠近点A),点F为线段CD的三等分点(靠近点C),且CE⊥AB.将△BCE沿CE对折,BC边与AD边交于点G,且DC=DG.
(1)证明:四边形AECF为矩形;
(2)求四边形AECG的面积.
20.如图,AB是⊙O的直径,C,D是⊙O上的点,且,AD分别与BC,OC相交于点E,F.
(1)求证:CB平分∠ABD;
(2)若AB=8,AD=6,求CF的长.
答案解析部分
C 2.C 3.C 4.A 5.A 6.B 7.D 8.A 9.C
10答案为. :1
11答案为.1:3
12答案为.
13答案为.
14答案为.2
15.解:∵四边形 四边形 ,
∴ , , .
∴ , , .
16.这个区域的实际周长480cm,面积8000cm2.
17.根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形,相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
①四条边成比例的两个凸四边形相似;( 假 命题)
②三个角分别相等的两个凸四边形相似;( 假 命题)
③两个大小不同的正方形相似.( 真 命题)
(2)如图,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,.求证:四边形ABCD与四边形A1B1C1D1相似.
【解答】(1)解:①四条边成比例的两个凸四边形相似,是假命题,角不一定相等;
②三个角分别相等的两个凸四边形相似,是假命题,边不一定成比例;
③两个大小不同的正方形相似,是真命题;
故答案为:假,假,真;
(2)证明:如图,连接BD,B1D1.
∵∠BCD=∠B1C1D1,且,
∴△BCD∽△B1C1D1,
∴∠CDB=∠C1D1B1,∠C1B1D1=∠CBD,
∵,
∴,
∵∠ABC=∠A1B1C1,
∴∠ABD=∠A1B1D1,
∴△ABD∽△A1B1D1,
∴,
∴∠A=∠A1,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,
∴四边形ABCD与四边形A1B1C1D1相似.
18.在人体躯干和身高的比例上,肚脐是理想的黄金分割点,即(下半身长m与身高l)比例越接近0.618越给人以美感,某女士身高165cm,下半身长(脚底到肚脐的高度)与身高的比值是0.60,为尽可能达到匀称的效果,她应该选择约多少厘米的高跟鞋看起来更美.(结果保留整数)
【解答】解:根据已知条件可知:
下半身长是165×0.6=99(厘米),
设需要穿的高跟鞋为y厘米,则根据黄金分割定义,得
=0.618,
解得:y≈8,
经检验y≈8是原方程的根,
答:她应该选择大约8厘米的高跟鞋.
19.(1)证明:∵ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵点E为线段AB的三等分点(靠近点A),
∴AE=AB,
∵点F为线段CD的三等分点(靠近点C),
∴CF=CD,
∴AE=CF,
又∵AE∥CF,
∴四边形AECF为平行四边形,
∵CE⊥AB,
∴四边形AECF为矩形;
(2)∵AB=3,
∴AE=CF=1,BE=2,
∵将△BCE沿CE对折得到△ECB',
∴B'E=BE=2,
∴AB'=1,
∵DC=DG=3,
∴∠DGC=∠DCG,
∵BB'∥CD,
∴∠DCG=∠B',
∴∠B'=∠DGC,
∵∠DGC=∠B'GA,
∴∠B'=∠B'GA,
∴AB'=AG=1,
∴DA=BC=B'C=4,
∵AB'∥CD,
∴,
∴,
∴B'G=1,
∴△AGB'是等边三角形,
∴A B'=AG=B'G=1,
作GH⊥A B'于H,
则AH=A B'=,
∴GH=,
在Rt△BCE中,BC=4,BE=2,
∴EC==2,
∴S四边形AECG=S△EB'C-S△AB'G=.
20.(1)证明:∵
∴∠OCB=∠DBC,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OBC=∠DBC,
∴CB平分∠ABD;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
由勾股定理得:,
∵,AO=BO,
∴AF=DF,
∴,
∵直径AB=8,
∴OC=OB=4,
∴CF=OC﹣OF=
1 / 3
