2021-2022学年苏科版数学七年级下册7.3图形的平移同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学七年级下册7.3图形的平移同步练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 742.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 15:36:48 | ||
图片预览



文档简介
7.3 图形的平移
一、单选题
1.在以下现象中,属于平移的是( )
①在荡秋千的小朋友的运动;②坐观光电梯上升的过程;③钟面上秒针的运动;④生产过程中传送带上的电视机的移动过程.
A. ①② B. ②④ C. ②③ D. ③④
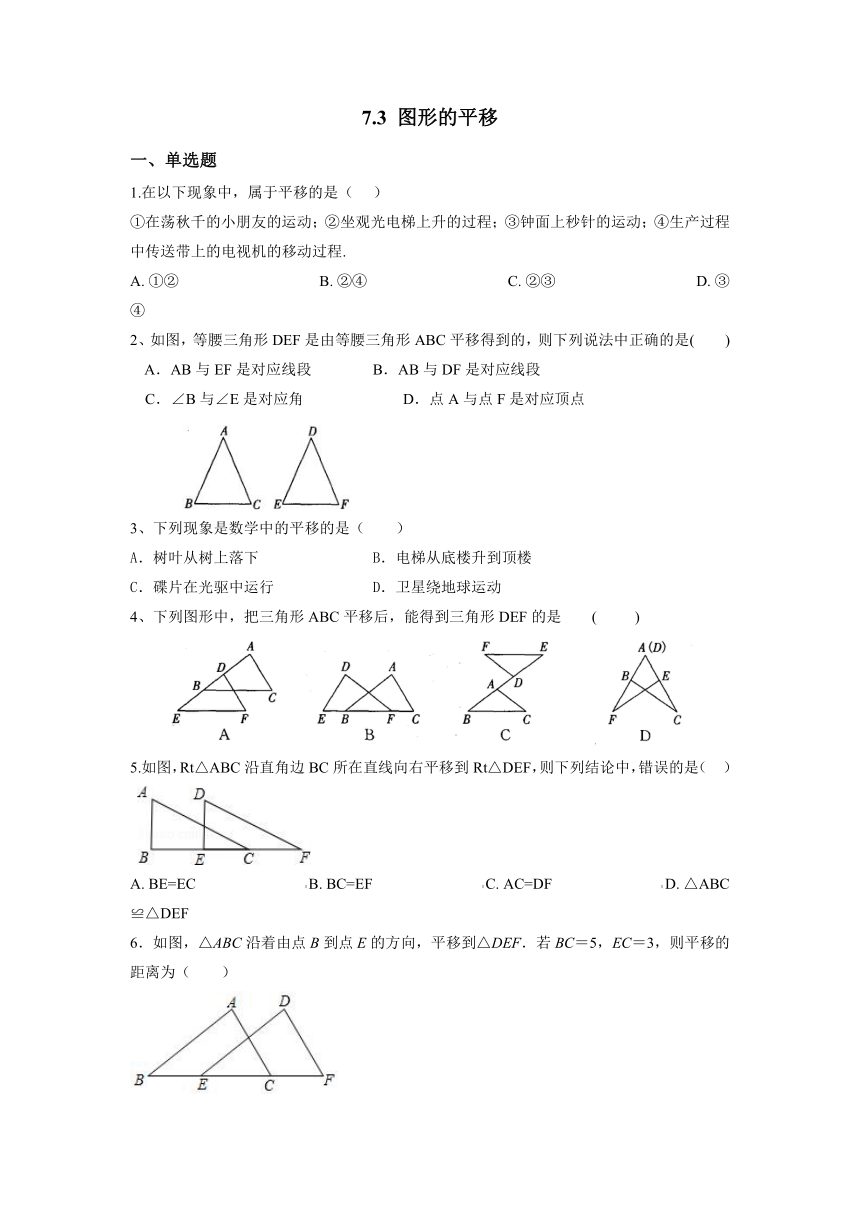
2、如图,等腰三角形DEF是由等腰三角形ABC平移得到的,则下列说法中正确的是( )
A.AB与EF是对应线段 B.AB与DF是对应线段
C.∠B与∠E是对应角 D.点A与点F是对应顶点
3、下列现象是数学中的平移的是( )
A.树叶从树上落下 B.电梯从底楼升到顶楼
C.碟片在光驱中运行 D.卫星绕地球运动
4、下列图形中,把三角形ABC平移后,能得到三角形DEF的是 ( )
5.如图,Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF,则下列结论中,错误的是( )
A. BE=EC B. BC=EF C. AC=DF D. △ABC≌△DEF
6.如图,△ABC沿着由点B到点E的方向,平移到△DEF.若BC=5,EC=3,则平移的距离为( )
A.7 B.5 C.3 D.2
7.如图,两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起,固定三角形ABC不动,将三角形DEF向右平移,当点E和点C重合时,停止移动,设DE交AC于G.给出下列结论:
①四边形ABEG的面积与CGDF的面积相等;
②AD∥EC,且AD=EC,
则( )
A.①,②都正确 B.①正确,②错误
C.①,②都错误 D.①错误,②正确
8.身高1.62米的小明乘升降电梯从1楼上升到3楼,则此时小明的身高为( )
A.1.62米 B.2.62米 C.3.62米 D.4.62米
9.如图所示,把长方形ABCD的斜对角AC等分成6段,以每一段为斜对角线作6个小长方形,若AB=1,BC=2.5,则6个小长方形的周长之和等于( )
A. 3.5 B. 3 C. 7 D. 5
10.如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2m , 则两条小路的总面积是( )m2
A. 108 B. 104 C. 100 D. 98
二、填空题
11、如图所示,△ABC经过平移得到△A’B’C’,图中△_________与△_________大小形状不变,线段AB与A’B’的位置关系是________,线段C C’与B B’的位置关系是________.
(11题) (12题)
12、在高3米,水平距离为4米的楼梯表面铺地毯,地毯的长度至少需要 米.
13、如图,将向右平移得到,如果,,则平移的距离是 .
14.如图,有一块长为32 m、宽为24 m的长方形草坪,其中有两条直道将草坪分为四块,则分成的四块草坪的总面积是________m2 .
三、解答题
15.(2021·全国七年级)平移三角形ABC,使点A移动到点A′,画出平移后的三角形A′B′C′.
16.(2020·浙江杭州市·七年级期中)在图中,利用网格点和三角板画图或计算:
(1)在给定方格纸中画出平移后的,并回答是如何平移的;
(2)图中与A′C′的关系怎样?
(3)记网格的边长为1,则的面积为多少?
17.(2021·全国九年级)如图,在方格纸中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点就是小正方形的格点.
(1)将△ABC向右平移3个单位长度再向下平移1个单位长度,得到△DEF(A与D、B与E、C与F对应),请在方格纸中画出△DEF;
(2)在(1)的条件下,连接AD、CF,AD与CF之间的关系是 ;
(3)在(1)的条件下,连接AE和CE,求△ACE的面积S.
18如图,一块边长为8米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
(1)请利用平移的知识求出种花草的面积.
(2)若空白的部分种植花草共花费了4620元,则每平方米种植花草的费用是多少元?
19如图所示,△ABC平移后得到△DEF.
(1)若∠A=80°,∠E=60°,求∠C的度数;
(2)若AC=BC,BC与DF相交于点O,则OD与OB相等吗?说明理由.
参考答案
一、单选题
1.B 2.C 3.B 4.A 5.A 6.D 7.B 8.A 9. C 10. C
二、填空题
11、【答案】ABC A’B’C’ 平行 平行
12、答案为:7.
13、答案为:2.
14.【答案】 660.
三、解答题
15.见解析
【详解】
解:如图:连接AA′,在AA′在一条直线上CC′=AA′,得到C′;
再作BB′∥AA′且BB′=AA′,最后顺次连接得到△A′B′C′即为所求三角形.
16.(1)见解析;(2)AC∥A′C′且AC=A′C′;(3)8
【详解】
解:(1)如图所示:△ABC向左平移7个单位,向下平移1个单位得到△A′B′C′;
(2)由题意可知:
AC∥A′C′且AC=A′C′;
(3)S△A′B′C′=×4×4=8.
17.(1)答案见解析;(2)AD//CF,AD=CF;(3)9.5
【详解】
解:(1)如图所示:△DEF即为所求;
(2)如图所示:AD与CF之间的关系是:AD//CF,AD=CF;
故答案为:AD//CF,AD=CF;.
(3)△ACE的面积S=4×53×41×41×5=9.5.
19【答案】 解:(1)∵△ABC平移后得到△DEF,
∴∠ABC=∠E=60°,
在△ABC中,∠C=180°﹣∠A﹣∠ABC=180°﹣80°﹣60°=40°;
(2)OD=OB.
理由如下:∵AC=BC,
∴∠A=∠ABC,
由平移的性质得,∠A=∠EDF,
∴∠ABC=∠EDF,
∴OD=OB.
一、单选题
1.在以下现象中,属于平移的是( )
①在荡秋千的小朋友的运动;②坐观光电梯上升的过程;③钟面上秒针的运动;④生产过程中传送带上的电视机的移动过程.
A. ①② B. ②④ C. ②③ D. ③④
2、如图,等腰三角形DEF是由等腰三角形ABC平移得到的,则下列说法中正确的是( )
A.AB与EF是对应线段 B.AB与DF是对应线段
C.∠B与∠E是对应角 D.点A与点F是对应顶点
3、下列现象是数学中的平移的是( )
A.树叶从树上落下 B.电梯从底楼升到顶楼
C.碟片在光驱中运行 D.卫星绕地球运动
4、下列图形中,把三角形ABC平移后,能得到三角形DEF的是 ( )
5.如图,Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF,则下列结论中,错误的是( )
A. BE=EC B. BC=EF C. AC=DF D. △ABC≌△DEF
6.如图,△ABC沿着由点B到点E的方向,平移到△DEF.若BC=5,EC=3,则平移的距离为( )
A.7 B.5 C.3 D.2
7.如图,两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起,固定三角形ABC不动,将三角形DEF向右平移,当点E和点C重合时,停止移动,设DE交AC于G.给出下列结论:
①四边形ABEG的面积与CGDF的面积相等;
②AD∥EC,且AD=EC,
则( )
A.①,②都正确 B.①正确,②错误
C.①,②都错误 D.①错误,②正确
8.身高1.62米的小明乘升降电梯从1楼上升到3楼,则此时小明的身高为( )
A.1.62米 B.2.62米 C.3.62米 D.4.62米
9.如图所示,把长方形ABCD的斜对角AC等分成6段,以每一段为斜对角线作6个小长方形,若AB=1,BC=2.5,则6个小长方形的周长之和等于( )
A. 3.5 B. 3 C. 7 D. 5
10.如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2m , 则两条小路的总面积是( )m2
A. 108 B. 104 C. 100 D. 98
二、填空题
11、如图所示,△ABC经过平移得到△A’B’C’,图中△_________与△_________大小形状不变,线段AB与A’B’的位置关系是________,线段C C’与B B’的位置关系是________.
(11题) (12题)
12、在高3米,水平距离为4米的楼梯表面铺地毯,地毯的长度至少需要 米.
13、如图,将向右平移得到,如果,,则平移的距离是 .
14.如图,有一块长为32 m、宽为24 m的长方形草坪,其中有两条直道将草坪分为四块,则分成的四块草坪的总面积是________m2 .
三、解答题
15.(2021·全国七年级)平移三角形ABC,使点A移动到点A′,画出平移后的三角形A′B′C′.
16.(2020·浙江杭州市·七年级期中)在图中,利用网格点和三角板画图或计算:
(1)在给定方格纸中画出平移后的,并回答是如何平移的;
(2)图中与A′C′的关系怎样?
(3)记网格的边长为1,则的面积为多少?
17.(2021·全国九年级)如图,在方格纸中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点就是小正方形的格点.
(1)将△ABC向右平移3个单位长度再向下平移1个单位长度,得到△DEF(A与D、B与E、C与F对应),请在方格纸中画出△DEF;
(2)在(1)的条件下,连接AD、CF,AD与CF之间的关系是 ;
(3)在(1)的条件下,连接AE和CE,求△ACE的面积S.
18如图,一块边长为8米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
(1)请利用平移的知识求出种花草的面积.
(2)若空白的部分种植花草共花费了4620元,则每平方米种植花草的费用是多少元?
19如图所示,△ABC平移后得到△DEF.
(1)若∠A=80°,∠E=60°,求∠C的度数;
(2)若AC=BC,BC与DF相交于点O,则OD与OB相等吗?说明理由.
参考答案
一、单选题
1.B 2.C 3.B 4.A 5.A 6.D 7.B 8.A 9. C 10. C
二、填空题
11、【答案】ABC A’B’C’ 平行 平行
12、答案为:7.
13、答案为:2.
14.【答案】 660.
三、解答题
15.见解析
【详解】
解:如图:连接AA′,在AA′在一条直线上CC′=AA′,得到C′;
再作BB′∥AA′且BB′=AA′,最后顺次连接得到△A′B′C′即为所求三角形.
16.(1)见解析;(2)AC∥A′C′且AC=A′C′;(3)8
【详解】
解:(1)如图所示:△ABC向左平移7个单位,向下平移1个单位得到△A′B′C′;
(2)由题意可知:
AC∥A′C′且AC=A′C′;
(3)S△A′B′C′=×4×4=8.
17.(1)答案见解析;(2)AD//CF,AD=CF;(3)9.5
【详解】
解:(1)如图所示:△DEF即为所求;
(2)如图所示:AD与CF之间的关系是:AD//CF,AD=CF;
故答案为:AD//CF,AD=CF;.
(3)△ACE的面积S=4×53×41×41×5=9.5.
19【答案】 解:(1)∵△ABC平移后得到△DEF,
∴∠ABC=∠E=60°,
在△ABC中,∠C=180°﹣∠A﹣∠ABC=180°﹣80°﹣60°=40°;
(2)OD=OB.
理由如下:∵AC=BC,
∴∠A=∠ABC,
由平移的性质得,∠A=∠EDF,
∴∠ABC=∠EDF,
∴OD=OB.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
