广东省新兴县惠能中学高二数学《3.2.2直线的两点式方程》课件
文档属性
| 名称 | 广东省新兴县惠能中学高二数学《3.2.2直线的两点式方程》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 202.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-28 14:54:52 | ||
图片预览






文档简介
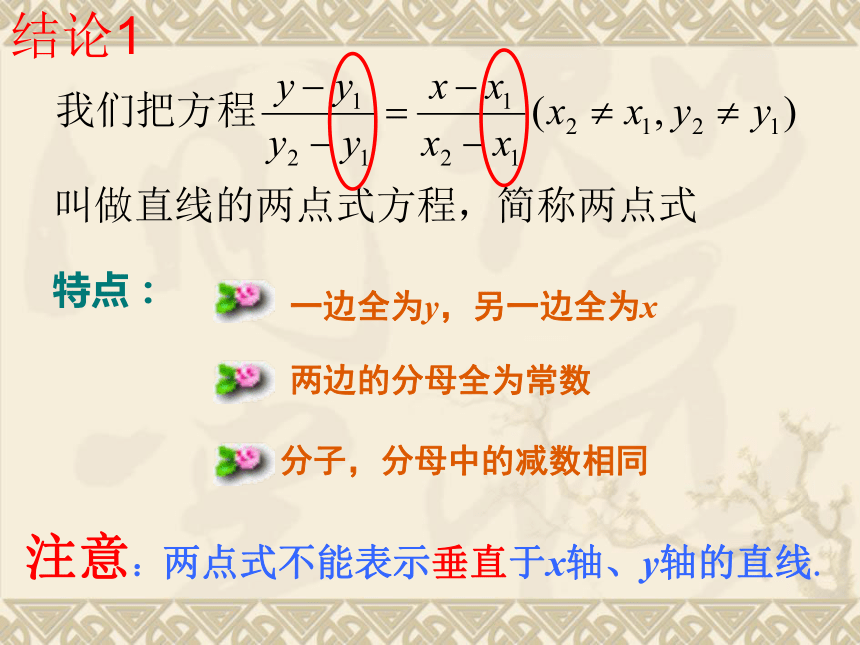
课件16张PPT。3.2.2直线的两点式方程复习旧知经过这两点的直线的斜率把斜率公式代入点斜式方程可以得到: 又y1≠y2,上式可写成探究1:注意:两点式不能表示垂直于x轴、y轴的直线.特点:分子,分母中的减数相同一边全为y,另一边全为x两边的分母全为常数 结论1练习1:求经过下列两点的直线的两点式方程, 再化为一般式方程.
(1) P (2,1),Q (0,-3)
(2) C(-4,-5),D (0,0)
(3) A (0,5),B (5,0)已知三角形的三个顶点A(-5,0),B(3,-3),C(0,2),求BC边所在直线的方程,以及该边上中线所在直线的方程.解:过B(3,-3),C(0,2)
的两点式方程为: 整理得:5x+3y-6=0因此BC边所在直线的方程为:5x+3y-6=0 例1由中点坐标公式: M为AB的中点,由中点坐标公式得到M的坐标为:整理得: x+13y+5=0 这就是BC边上的中线所在直线的方程 A(-5,0),B(3,-3) C(0,2)练习2:若三角形ABC的顶点A(-5,0),
B(3,-2),C(1,2),则经过AB,BC两边中
点的直线方程为________. x-3y-2=0 探究2: 已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求直线l的方程.解:将A,B两点的坐标代入两点式可得: 若直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,则这条直线l的方程为:说明:
(1)直线与x轴的交点(a,0)的横坐标a叫做直线在x轴的截距,此时直线在y轴的截距是b。 (3)截距式适用于横、纵截距都存在且都不为0的直线.即直线不能垂直于x轴和y轴,不能过原点。(2)这个方程由直线在x轴和y轴的截距确定,所以叫做直线方程的截距式方程,简称截距式。纵截距横截距结论2练习3:根据下列条件求直线方程(1)在x轴上的截距为2,在y轴上的截距是3;(2)在x轴上的截距为-5,在y轴上的截距是6;由截距式得: 整理得:由截距式得: 整理得:例2:根据下列条件,求直线的方程(1)过点(0,5),且在两坐标轴上的截距之和为2(2)过点(5,0),且在两坐标轴上的截距之差为2解:所以有: 因为直线过点
(0,5),且在两坐标轴上的截距之和为2, 解出:a=-3,b=5即5x-3y+15=0 因为直线过点
(5,0),且在两坐标轴上的截距之差为2, (2)过点(5,0),且在两坐标轴上的截距之差为2解:所以有: 解出:a=5,b=3或即3x+5y-15=0或7x+5y-35=0 a=5,b=7解:练习4 :过(1,2)并且在两个坐标轴上的截距相等的直线有几条?小结纵横截距a≠0,b≠0作业P100
A组 第4、9题
(1) P (2,1),Q (0,-3)
(2) C(-4,-5),D (0,0)
(3) A (0,5),B (5,0)已知三角形的三个顶点A(-5,0),B(3,-3),C(0,2),求BC边所在直线的方程,以及该边上中线所在直线的方程.解:过B(3,-3),C(0,2)
的两点式方程为: 整理得:5x+3y-6=0因此BC边所在直线的方程为:5x+3y-6=0 例1由中点坐标公式: M为AB的中点,由中点坐标公式得到M的坐标为:整理得: x+13y+5=0 这就是BC边上的中线所在直线的方程 A(-5,0),B(3,-3) C(0,2)练习2:若三角形ABC的顶点A(-5,0),
B(3,-2),C(1,2),则经过AB,BC两边中
点的直线方程为________. x-3y-2=0 探究2: 已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求直线l的方程.解:将A,B两点的坐标代入两点式可得: 若直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,则这条直线l的方程为:说明:
(1)直线与x轴的交点(a,0)的横坐标a叫做直线在x轴的截距,此时直线在y轴的截距是b。 (3)截距式适用于横、纵截距都存在且都不为0的直线.即直线不能垂直于x轴和y轴,不能过原点。(2)这个方程由直线在x轴和y轴的截距确定,所以叫做直线方程的截距式方程,简称截距式。纵截距横截距结论2练习3:根据下列条件求直线方程(1)在x轴上的截距为2,在y轴上的截距是3;(2)在x轴上的截距为-5,在y轴上的截距是6;由截距式得: 整理得:由截距式得: 整理得:例2:根据下列条件,求直线的方程(1)过点(0,5),且在两坐标轴上的截距之和为2(2)过点(5,0),且在两坐标轴上的截距之差为2解:所以有: 因为直线过点
(0,5),且在两坐标轴上的截距之和为2, 解出:a=-3,b=5即5x-3y+15=0 因为直线过点
(5,0),且在两坐标轴上的截距之差为2, (2)过点(5,0),且在两坐标轴上的截距之差为2解:所以有: 解出:a=5,b=3或即3x+5y-15=0或7x+5y-35=0 a=5,b=7解:练习4 :过(1,2)并且在两个坐标轴上的截距相等的直线有几条?小结纵横截距a≠0,b≠0作业P100
A组 第4、9题
