2021—2022学年人教版八年级数学下册18.1平行四边形课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册18.1平行四边形课后练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 385.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 00:00:00 | ||
图片预览


文档简介
2021——2022学年度人教版八年级数学下册 第十八章平行四边形
18.1平行四边形课后练习
一、选择题
1.下列条件中,不能判定一个四边形是平行四边形的是( )
A.一组对边平行且相等 B.对角线互相平分
C.两组对角分别相等 D.一组对边平行,另一组对边相等
2.平行四边形ABCD中,若∠A=2∠B,则∠C的度数为( )
A.120° B.60° C.30° D.15°
3.在四边形中,与相交于点,且,给出下列条件:①;②;③;④.从中选1个作为条件,能使四边形为平行四边形的选法有( )
A.种 B.种 C.种 D.种
4.在平行四边形ABCD中,∠A ∶∠ B ∶∠ C ∶∠ D的值可以是( )
A.1∶2∶3∶4 B.1∶2∶2∶1 C.2∶2∶1∶1 D.1∶2∶1∶2
5.如图,在平行四边形中,是的中点,,,,则的长为( )
A. B. C. D.
6.如图,在 ABCD中,若EFAD,OHCD,EF与GH相交于点O,则图中的平行四边形一共有( )
A.4个 B.5个 C.8个 D.9个
7.如图,平行四边形ABCD中,E、F分别在边BC、AD上,添加条件后不能使AE=CF的是( )
A.BE=DF B.AE∥CF C.AF=AE D.AF=EC
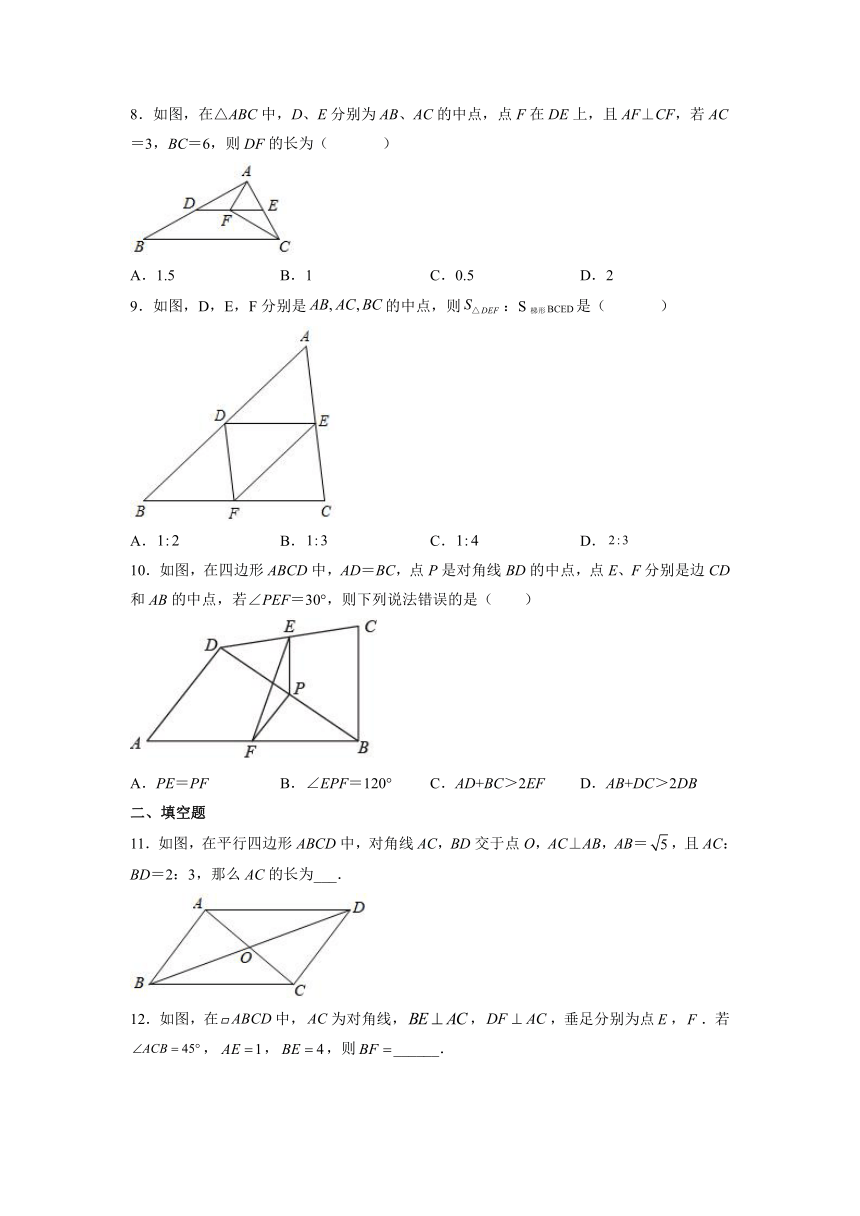
8.如图,在△ABC中,D、E分别为AB、AC的中点,点F在DE上,且AF⊥CF,若AC=3,BC=6,则DF的长为( )
A.1.5 B.1 C.0.5 D.2
9.如图,D,E,F分别是的中点,则:S梯形BCED是( )
A. B. C. D.
10.如图,在四边形ABCD中,AD=BC,点P是对角线BD的中点,点E、F分别是边CD和AB的中点,若∠PEF=30°,则下列说法错误的是( )
A.PE=PF B.∠EPF=120° C.AD+BC>2EF D.AB+DC>2DB
二、填空题
11.如图,在平行四边形ABCD中,对角线AC,BD交于点O,AC⊥AB,AB=,且AC:BD=2:3,那么AC的长为___.
12.如图,在中,为对角线,,,垂足分别为点,.若,,,则______.
13.如图,点P为平行四边形ABCD内一点(点P不在BD上),过点P作EF∥AD,HG∥AB,与各边分别相交于点E、F、G、H.若四边形AEPH的面积为2,四边形PGCF的面积为4,则△PBD的面积=___.
14.如图,在中,为中线,和分别为和的一条高.若,,,则__________.
15.如图,点,,分别是的边,,的中点,如果,那么等于______.
三、解答题
16.如图,在中,与交于点,,,,求长.
17.如图,在中,、为上两点,.求证:.
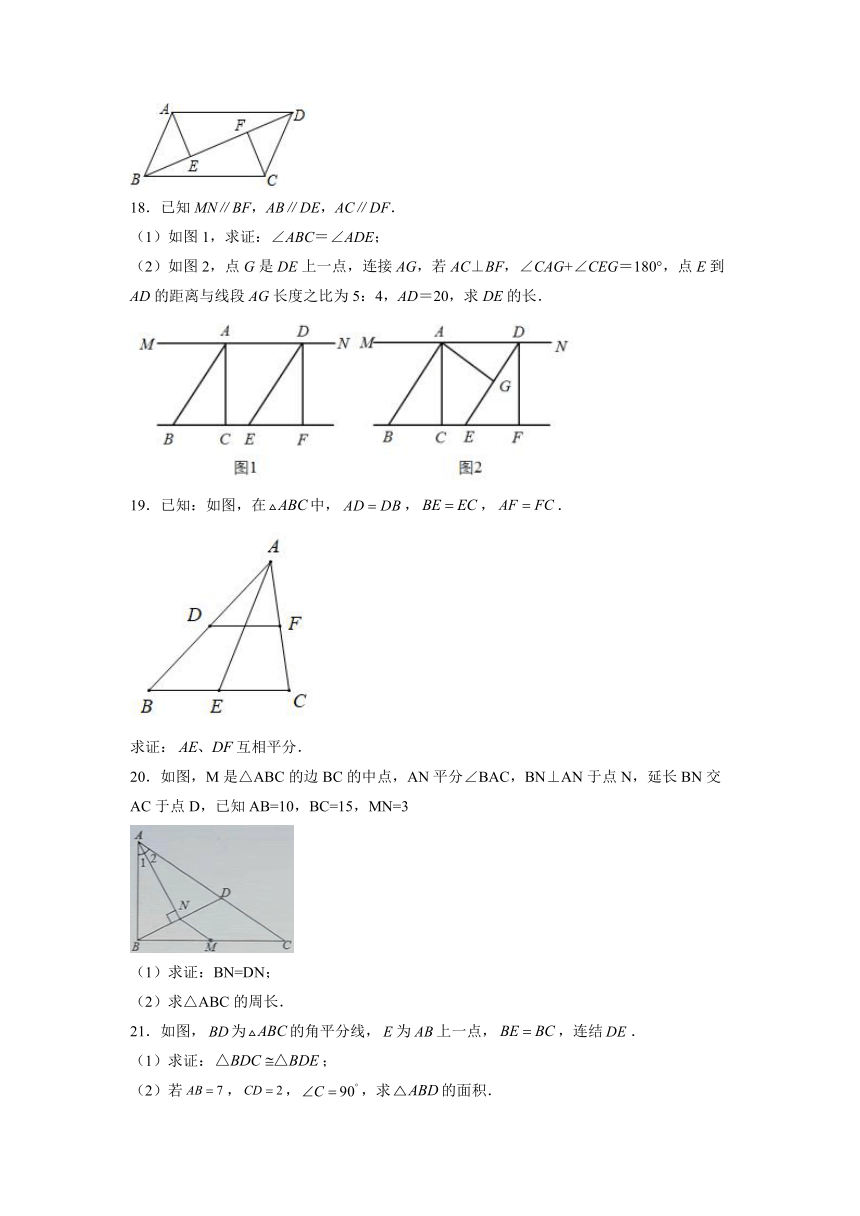
18.已知MN∥BF,AB∥DE,AC∥DF.
(1)如图1,求证:∠ABC=∠ADE;
(2)如图2,点G是DE上一点,连接AG,若AC⊥BF,∠CAG+∠CEG=180°,点E到AD的距离与线段AG长度之比为5:4,AD=20,求DE的长.
19.已知:如图,在中,,,.
求证:互相平分.
20.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
(1)求证:BN=DN;
(2)求△ABC的周长.
21.如图,为的角平分线,为上一点,,连结.
(1)求证:;
(2)若,,,求的面积.
22.如图,,是四边形的对角线的三等分点,,的延长线分别平分,,交点分别为点,.
(1)求证:;
(2)求证:四边形是平行四边形.
23.如图,平行四边形ABCD的对角线AC,BD交于点O,M,N分别是AB,AD的中点.
(1)求证:四边形AMON是平行四边形;
(2)若AC=6,BD=4,∠AOB=90°,求NO的长度.
【参考答案】
1.D 2.A 3.B 4.D 5.D 6.D 7.C 8.A 9.B 10.D
11.4
12.5
13.1
14.2
15.50°
16.解:∵四边形ABCD是平行四边形,∠DAC=45°,
∴∠ACB=∠DAC=45°,OA=AC=1,
∵AB⊥AC,
∴△ABC是等腰直角三角形,
∴AB=AC=2,
在Rt△AOB中,根据勾股定理得OB=,
∴BD=2BO=2.
17.证明:四边形平行四边形,
,,
.
在与中,
,
,
,
.
18.解:(1)∵,,
∴,,
∴;
(2)∵,,
∴四边形ABED为平行四边形,
∵,
∴点E到AD的距离为AC,
∵
∴根据四边形内角和可得:,
由平行四边形等面积法可得:,
根据题意可得:,
∴,
∵,
∴.
19.
证明:连接,
∵AD=DB,BE=EC,
∴,
∵BE=EC,AF=FC,
∴,
∴四边形ADEF是平行四边形,
∴AE,DF互相平分.
20.解:(1)证明:在△ABN和△ADN中,∵,
∴△ABN≌△ADN(ASA).
∴BN=DN.
(2)∵△ABN≌△ADN,∴AD=AB=10,DN=NB.
又∵点M是BC中点,∴MN是△BDC的中位线.
∴CD=2MN=6.
∴△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.
21.(1)∵平分,
∴,
∴在和中,
,,,
∴≌;
(2)∵≌,
∴,,
∴.
22.证明:(1)连接交于,连接,,
∵,是的三等分点
∴
是中点,
是的一条中位线,
,即,
同理:,
四边形是平行四边形.
∴,,
∴,即
(2)由(1)得:,
又,
,即
四边形是平行四边形.
23.(1)∵四边形是平行四边形,
∴AO=OC,BO=OD.
∵,分别是、的中点,
∴,,
∴,,
∴四边形是平行四边形;
(2)解:∵四边形是平行四边形,
∴,.
∵,,
∴,.
∵,
∴
∵是的中点,,
∴,
∴
18.1平行四边形课后练习
一、选择题
1.下列条件中,不能判定一个四边形是平行四边形的是( )
A.一组对边平行且相等 B.对角线互相平分
C.两组对角分别相等 D.一组对边平行,另一组对边相等
2.平行四边形ABCD中,若∠A=2∠B,则∠C的度数为( )
A.120° B.60° C.30° D.15°
3.在四边形中,与相交于点,且,给出下列条件:①;②;③;④.从中选1个作为条件,能使四边形为平行四边形的选法有( )
A.种 B.种 C.种 D.种
4.在平行四边形ABCD中,∠A ∶∠ B ∶∠ C ∶∠ D的值可以是( )
A.1∶2∶3∶4 B.1∶2∶2∶1 C.2∶2∶1∶1 D.1∶2∶1∶2
5.如图,在平行四边形中,是的中点,,,,则的长为( )
A. B. C. D.
6.如图,在 ABCD中,若EFAD,OHCD,EF与GH相交于点O,则图中的平行四边形一共有( )
A.4个 B.5个 C.8个 D.9个
7.如图,平行四边形ABCD中,E、F分别在边BC、AD上,添加条件后不能使AE=CF的是( )
A.BE=DF B.AE∥CF C.AF=AE D.AF=EC
8.如图,在△ABC中,D、E分别为AB、AC的中点,点F在DE上,且AF⊥CF,若AC=3,BC=6,则DF的长为( )
A.1.5 B.1 C.0.5 D.2
9.如图,D,E,F分别是的中点,则:S梯形BCED是( )
A. B. C. D.
10.如图,在四边形ABCD中,AD=BC,点P是对角线BD的中点,点E、F分别是边CD和AB的中点,若∠PEF=30°,则下列说法错误的是( )
A.PE=PF B.∠EPF=120° C.AD+BC>2EF D.AB+DC>2DB
二、填空题
11.如图,在平行四边形ABCD中,对角线AC,BD交于点O,AC⊥AB,AB=,且AC:BD=2:3,那么AC的长为___.
12.如图,在中,为对角线,,,垂足分别为点,.若,,,则______.
13.如图,点P为平行四边形ABCD内一点(点P不在BD上),过点P作EF∥AD,HG∥AB,与各边分别相交于点E、F、G、H.若四边形AEPH的面积为2,四边形PGCF的面积为4,则△PBD的面积=___.
14.如图,在中,为中线,和分别为和的一条高.若,,,则__________.
15.如图,点,,分别是的边,,的中点,如果,那么等于______.
三、解答题
16.如图,在中,与交于点,,,,求长.
17.如图,在中,、为上两点,.求证:.
18.已知MN∥BF,AB∥DE,AC∥DF.
(1)如图1,求证:∠ABC=∠ADE;
(2)如图2,点G是DE上一点,连接AG,若AC⊥BF,∠CAG+∠CEG=180°,点E到AD的距离与线段AG长度之比为5:4,AD=20,求DE的长.
19.已知:如图,在中,,,.
求证:互相平分.
20.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
(1)求证:BN=DN;
(2)求△ABC的周长.
21.如图,为的角平分线,为上一点,,连结.
(1)求证:;
(2)若,,,求的面积.
22.如图,,是四边形的对角线的三等分点,,的延长线分别平分,,交点分别为点,.
(1)求证:;
(2)求证:四边形是平行四边形.
23.如图,平行四边形ABCD的对角线AC,BD交于点O,M,N分别是AB,AD的中点.
(1)求证:四边形AMON是平行四边形;
(2)若AC=6,BD=4,∠AOB=90°,求NO的长度.
【参考答案】
1.D 2.A 3.B 4.D 5.D 6.D 7.C 8.A 9.B 10.D
11.4
12.5
13.1
14.2
15.50°
16.解:∵四边形ABCD是平行四边形,∠DAC=45°,
∴∠ACB=∠DAC=45°,OA=AC=1,
∵AB⊥AC,
∴△ABC是等腰直角三角形,
∴AB=AC=2,
在Rt△AOB中,根据勾股定理得OB=,
∴BD=2BO=2.
17.证明:四边形平行四边形,
,,
.
在与中,
,
,
,
.
18.解:(1)∵,,
∴,,
∴;
(2)∵,,
∴四边形ABED为平行四边形,
∵,
∴点E到AD的距离为AC,
∵
∴根据四边形内角和可得:,
由平行四边形等面积法可得:,
根据题意可得:,
∴,
∵,
∴.
19.
证明:连接,
∵AD=DB,BE=EC,
∴,
∵BE=EC,AF=FC,
∴,
∴四边形ADEF是平行四边形,
∴AE,DF互相平分.
20.解:(1)证明:在△ABN和△ADN中,∵,
∴△ABN≌△ADN(ASA).
∴BN=DN.
(2)∵△ABN≌△ADN,∴AD=AB=10,DN=NB.
又∵点M是BC中点,∴MN是△BDC的中位线.
∴CD=2MN=6.
∴△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.
21.(1)∵平分,
∴,
∴在和中,
,,,
∴≌;
(2)∵≌,
∴,,
∴.
22.证明:(1)连接交于,连接,,
∵,是的三等分点
∴
是中点,
是的一条中位线,
,即,
同理:,
四边形是平行四边形.
∴,,
∴,即
(2)由(1)得:,
又,
,即
四边形是平行四边形.
23.(1)∵四边形是平行四边形,
∴AO=OC,BO=OD.
∵,分别是、的中点,
∴,,
∴,,
∴四边形是平行四边形;
(2)解:∵四边形是平行四边形,
∴,.
∵,,
∴,.
∵,
∴
∵是的中点,,
∴,
∴
