六年级数学下册课件 - 7.2.长方体·正方体·圆柱·圆锥等体积不变问题 苏教版(共18张ppt)
文档属性
| 名称 | 六年级数学下册课件 - 7.2.长方体·正方体·圆柱·圆锥等体积不变问题 苏教版(共18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 149.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 16:27:52 | ||
图片预览





文档简介
(共18张PPT)
长方体·正方体·圆柱·圆锥等
体积不变问题
教学目标:
1.在掌握长方体、正方体、圆柱、圆锥等相关知识的基础上,初步学会解决体积不变问题的基本方法。
2.让学生经历观察、猜想、操作、交流和归纳等数学活动过程,学会解决体积不变问题。
3.培养学生勇于探索、积极学习的乐观精神。
教学过程设计
复习导入
新课探究
巩固反馈
课堂总结
布置作业
长
v
=a b h
v
正
=a
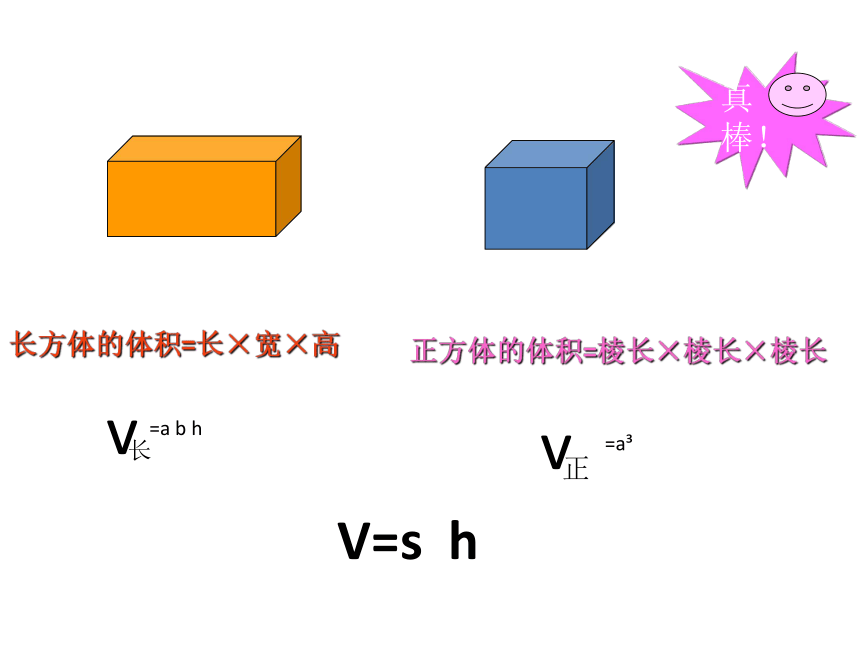
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
V=s h
真 棒!
圆柱的体积=底面积×高 V=sh
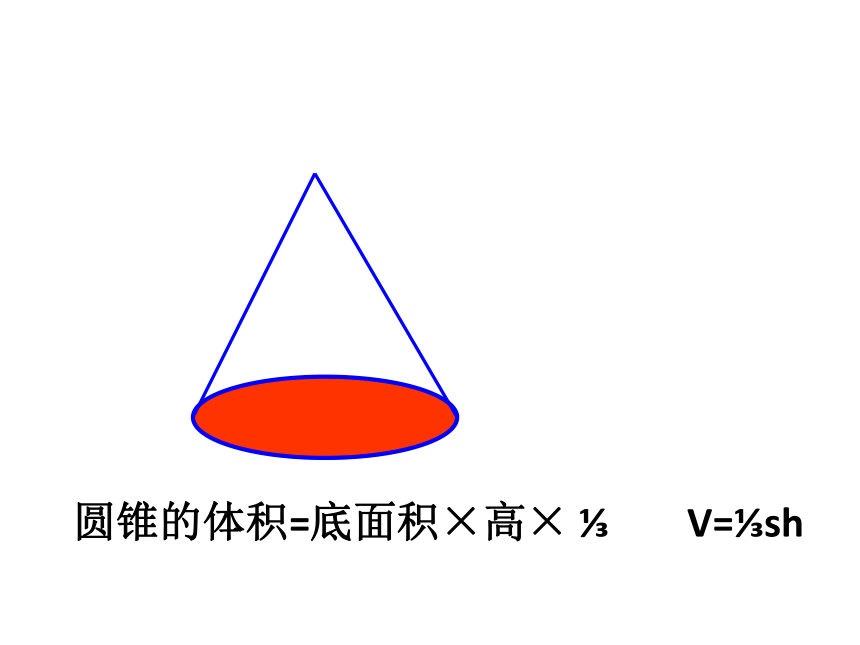
圆锥的体积=底面积×高× V= sh
1、你知道这些立体图形体积公式的变形公式吗?小组内说一说。
2、你能熟练运用吗?做一些题试试吧!
例1.把一个长15.7厘米,宽12厘米,高8厘米的长方体铁块熔 铸 成一个底面积是314平方厘米的圆柱,这个圆柱的高是多少厘米?
V=15.7×12×8
=1507.2(立方厘米)
h=1507.2÷314
=4.8(厘米)
答:这个圆柱的高为4.8厘米。
例2.一个圆锥形沙堆,底面积是78平方米,高是3米,用这堆沙子去填一个长6.5米,宽40分米的长方体沙坑,沙坑里的沙子厚度是多少米?
40分米=4米
V=78×3×
=78(立方米)
h=78÷(6.5×4)
=78÷26
=3(米)
答:沙坑里的沙子厚度是3米。
1、 你发现了什么?
2、怎样做正方体、长方体、圆柱、圆锥等体积不变的问题?
1.一个圆锥形沙堆,底面周长是12.56米,高2.4米。把它均匀的铺在一条长125.6米,宽4米的路上,平均厚度会超过2厘米吗?
2、用一个长30厘米,宽12厘米,高1分米的长方体铅块,铸造成一个底面直径4厘米,高12厘米的铅锥,最多能铸造多少个这样的铅锥?(π取3)
3、一个圆柱形水桶,底面半径为2分米,里面盛有80厘米的水。现将一个底面周长为62.8厘米的圆锥形铁块完全浸入水中(水未溢出),水面高度比原来上升了1∕16。这个圆锥形铁块的高是多少厘米?
通过这节课的学习,你有怎样的收获?在做体积不变问题时,我们应该怎样办?哪些点我们应该特别注意?
小结:
1、读完题先看单位是否统一,不统一的把单位统一起来。
2、找到所求的问题是什么,在练习本上写书所用公式。
3、根据所用公式找相应答案。
4、做题!
2、三分之一不要忘记了!
注意:
1、圆锥体积公式是什么?
2、把一个底面半径10厘米,高18厘米的圆锥形铁块完全浸没在一个底面长30厘米,宽20厘米的长方形水槽中,水面会上升多少厘米?
1、一个圆柱形铁块底面半径40厘米,高是4.5分米,将它铸造成一个底面半径6分米的圆锥,圆锥的高是多少分米?
课外作业
谢谢大家
再见
长方体·正方体·圆柱·圆锥等
体积不变问题
教学目标:
1.在掌握长方体、正方体、圆柱、圆锥等相关知识的基础上,初步学会解决体积不变问题的基本方法。
2.让学生经历观察、猜想、操作、交流和归纳等数学活动过程,学会解决体积不变问题。
3.培养学生勇于探索、积极学习的乐观精神。
教学过程设计
复习导入
新课探究
巩固反馈
课堂总结
布置作业
长
v
=a b h
v
正
=a
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
V=s h
真 棒!
圆柱的体积=底面积×高 V=sh
圆锥的体积=底面积×高× V= sh
1、你知道这些立体图形体积公式的变形公式吗?小组内说一说。
2、你能熟练运用吗?做一些题试试吧!
例1.把一个长15.7厘米,宽12厘米,高8厘米的长方体铁块熔 铸 成一个底面积是314平方厘米的圆柱,这个圆柱的高是多少厘米?
V=15.7×12×8
=1507.2(立方厘米)
h=1507.2÷314
=4.8(厘米)
答:这个圆柱的高为4.8厘米。
例2.一个圆锥形沙堆,底面积是78平方米,高是3米,用这堆沙子去填一个长6.5米,宽40分米的长方体沙坑,沙坑里的沙子厚度是多少米?
40分米=4米
V=78×3×
=78(立方米)
h=78÷(6.5×4)
=78÷26
=3(米)
答:沙坑里的沙子厚度是3米。
1、 你发现了什么?
2、怎样做正方体、长方体、圆柱、圆锥等体积不变的问题?
1.一个圆锥形沙堆,底面周长是12.56米,高2.4米。把它均匀的铺在一条长125.6米,宽4米的路上,平均厚度会超过2厘米吗?
2、用一个长30厘米,宽12厘米,高1分米的长方体铅块,铸造成一个底面直径4厘米,高12厘米的铅锥,最多能铸造多少个这样的铅锥?(π取3)
3、一个圆柱形水桶,底面半径为2分米,里面盛有80厘米的水。现将一个底面周长为62.8厘米的圆锥形铁块完全浸入水中(水未溢出),水面高度比原来上升了1∕16。这个圆锥形铁块的高是多少厘米?
通过这节课的学习,你有怎样的收获?在做体积不变问题时,我们应该怎样办?哪些点我们应该特别注意?
小结:
1、读完题先看单位是否统一,不统一的把单位统一起来。
2、找到所求的问题是什么,在练习本上写书所用公式。
3、根据所用公式找相应答案。
4、做题!
2、三分之一不要忘记了!
注意:
1、圆锥体积公式是什么?
2、把一个底面半径10厘米,高18厘米的圆锥形铁块完全浸没在一个底面长30厘米,宽20厘米的长方形水槽中,水面会上升多少厘米?
1、一个圆柱形铁块底面半径40厘米,高是4.5分米,将它铸造成一个底面半径6分米的圆锥,圆锥的高是多少分米?
课外作业
谢谢大家
再见
