六年级下册数学课件 1.2 圆柱的体积 北京版(25张PPT)
文档属性
| 名称 | 六年级下册数学课件 1.2 圆柱的体积 北京版(25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 18:31:38 | ||
图片预览








文档简介
(共25张PPT)
学习目标:
1.通过动手操作实验推导出圆柱体积的计算公式。
2.理解并掌握圆柱体积公式,能运用公式求圆柱的体积,并会解决简单的实际问题。
3.通过学生动脑动手,培养学生的观察分析的综合能力。
温故知新
(1) 圆面积公式是怎样推导出来的?
πr
r
S=πr ×r =π
S=π
圆的面积公式推导过程:
温故知新
(2)什么叫物体的体积?你学过哪些物体体积?公式是什么?通用的公式是什么?
长
v
=a b h
v
3
正
=a
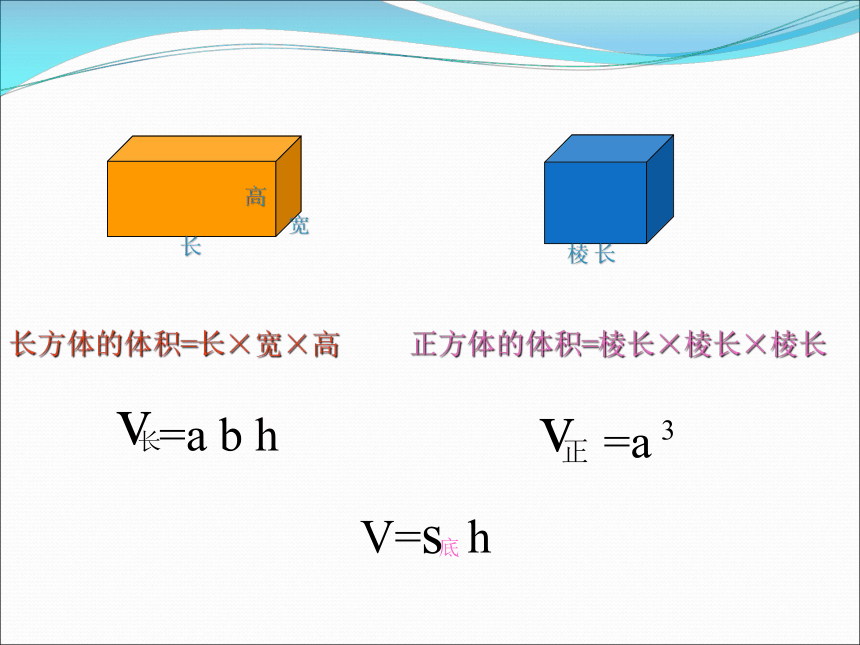
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
V=s h
底
长
宽
高
棱 长
怎样求它们的体积呢
新知探究
圆柱体积的大小与哪些条件有关?
归纳小结:
当高相等时,底面积越大,体积就(越大)。
当底面积相等时,高越长,体积就(越大)。
1.你是怎样转化圆柱学具的?
2.转化的两个物体什么变了?什么没变?
3. 它们的底面积相等吗?高相等吗?
4.试着推导圆柱的体积公式。
讨论题
圆柱的体积
平均分成的份数越多,拼成的图形就越接近(长方体)。
长方体的体积=?
长方体体积 =底面积×高
圆柱体积
=
=底面积×高
长方体的底面积等于圆柱的 底面积 ,
高等于圆柱的 高 。
V =Sh
V =s h
体积 = 底面积×高
上面长方体、正方体和圆柱的底面积都相等,高也相等,那它们的体积相等吗?为什么?
想一想:
要求圆柱的体积需要
知道什么条件?
知道S和h:
知道r和h:
知道d和h:
知道C和h:
V=Sh
V=πr2×h
V=π (C÷π÷2)2×h
(1)
(2)
(3)
考一考:
1.(求圆柱的体积,只列式不计算,并写出相应的公式)
V=s h
12×6
3.14 ×3 ×7
2
3.14 ×(6÷2) ×8
2
6
分
米
12平方分米
7分米
.
3分米
6分米
8分米
V=兀(d÷2)×h
2
V= 兀r × h
2
2.我是小法官:
1.正方体、长方体、圆柱体的底面积和高相等,他们体积也相等。( )
2.长方体、正方体、圆柱体的体积都 可以用 底面积乘高的方法来计算。( )
3.圆柱体的底面积越大,它的 体积越大。( )
4.圆柱体的高越长,它的体积越大。( )
5.如果圆柱体的底面半径扩大2倍,高不变,体积也扩大2倍.( )
√
×
×
×
√
运用所学的知识解决实际问题
一根圆柱形钢材,底面积是20平方厘米,高是1.5米。它的体积是多少?
V=sh
1.5米=150厘米
20×150=3000(立方厘米)
答:它的体积是3000立方厘米。
我们在计算和应用圆柱体有关知识时应注意些什么?
努力吧!
练习巩固 应用拓展
把一根长1.5分米的圆柱形钢材截成三段后,如图,表面积比原来增加9.6平方分米,这根钢材原来的体积是多少?
(9.6÷3)×1.5=4.8(立方分米)
答:这根钢材原来的体积是4.8立方分米
(9.6÷4)×1.5=3.6(立方分米)
答:这根钢材原来的体积是3.6立方分米
把一个马铃薯完全浸没在一个底面直径是20厘米,水深12厘米的圆柱形容器中,水没有溢出,且量得水面上升了3厘米。这个马铃薯的体积是多少立方厘米?
3cm
12cm
20cm
上升3厘米的水的体积=马铃薯的体积=底面积X高
3.14X(20÷2)
2
X3
= 942(立方厘米)
答:这个土豆的体积是942立方厘米。
本节课你有哪些收获?
学习目标:
1.通过动手操作实验推导出圆柱体积的计算公式。
2.理解并掌握圆柱体积公式,能运用公式求圆柱的体积,并会解决简单的实际问题。
3.通过学生动脑动手,培养学生的观察分析的综合能力。
温故知新
(1) 圆面积公式是怎样推导出来的?
πr
r
S=πr ×r =π
S=π
圆的面积公式推导过程:
温故知新
(2)什么叫物体的体积?你学过哪些物体体积?公式是什么?通用的公式是什么?
长
v
=a b h
v
3
正
=a
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
V=s h
底
长
宽
高
棱 长
怎样求它们的体积呢
新知探究
圆柱体积的大小与哪些条件有关?
归纳小结:
当高相等时,底面积越大,体积就(越大)。
当底面积相等时,高越长,体积就(越大)。
1.你是怎样转化圆柱学具的?
2.转化的两个物体什么变了?什么没变?
3. 它们的底面积相等吗?高相等吗?
4.试着推导圆柱的体积公式。
讨论题
圆柱的体积
平均分成的份数越多,拼成的图形就越接近(长方体)。
长方体的体积=?
长方体体积 =底面积×高
圆柱体积
=
=底面积×高
长方体的底面积等于圆柱的 底面积 ,
高等于圆柱的 高 。
V =Sh
V =s h
体积 = 底面积×高
上面长方体、正方体和圆柱的底面积都相等,高也相等,那它们的体积相等吗?为什么?
想一想:
要求圆柱的体积需要
知道什么条件?
知道S和h:
知道r和h:
知道d和h:
知道C和h:
V=Sh
V=πr2×h
V=π (C÷π÷2)2×h
(1)
(2)
(3)
考一考:
1.(求圆柱的体积,只列式不计算,并写出相应的公式)
V=s h
12×6
3.14 ×3 ×7
2
3.14 ×(6÷2) ×8
2
6
分
米
12平方分米
7分米
.
3分米
6分米
8分米
V=兀(d÷2)×h
2
V= 兀r × h
2
2.我是小法官:
1.正方体、长方体、圆柱体的底面积和高相等,他们体积也相等。( )
2.长方体、正方体、圆柱体的体积都 可以用 底面积乘高的方法来计算。( )
3.圆柱体的底面积越大,它的 体积越大。( )
4.圆柱体的高越长,它的体积越大。( )
5.如果圆柱体的底面半径扩大2倍,高不变,体积也扩大2倍.( )
√
×
×
×
√
运用所学的知识解决实际问题
一根圆柱形钢材,底面积是20平方厘米,高是1.5米。它的体积是多少?
V=sh
1.5米=150厘米
20×150=3000(立方厘米)
答:它的体积是3000立方厘米。
我们在计算和应用圆柱体有关知识时应注意些什么?
努力吧!
练习巩固 应用拓展
把一根长1.5分米的圆柱形钢材截成三段后,如图,表面积比原来增加9.6平方分米,这根钢材原来的体积是多少?
(9.6÷3)×1.5=4.8(立方分米)
答:这根钢材原来的体积是4.8立方分米
(9.6÷4)×1.5=3.6(立方分米)
答:这根钢材原来的体积是3.6立方分米
把一个马铃薯完全浸没在一个底面直径是20厘米,水深12厘米的圆柱形容器中,水没有溢出,且量得水面上升了3厘米。这个马铃薯的体积是多少立方厘米?
3cm
12cm
20cm
上升3厘米的水的体积=马铃薯的体积=底面积X高
3.14X(20÷2)
2
X3
= 942(立方厘米)
答:这个土豆的体积是942立方厘米。
本节课你有哪些收获?
