华东师大版七年级数学下册 9.1.2三角形的内角和与外角和 教案
文档属性
| 名称 | 华东师大版七年级数学下册 9.1.2三角形的内角和与外角和 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 150.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 08:18:45 | ||
图片预览

文档简介
三角形的内角和与外角和
教学目标
知识与技能
1、理解三角形的内角和、外角和以及外角的性质。
2、学会用简单的说理来计算三角形相关的角。
过程与方法
经历三角形内角和、外角和及性质的探索过程,培养实践能力及观察总结能力。
情感态度与价值观
在学习过程中,激发学生主动学习数学的兴趣,体验数学学习成功的喜悦。
重点难点
重点:三角形内角和定理的证明,三角形外角和定理与性质。
难点:三角形内角和定理和外角性质的证明方法。
教学设计
一、情境引入
同学们,在小学咱们曾经学过三角形的内角和是吧,是怎样总结出来的呢?把三个角剪下来重新拼一拼的。请一个同学来试一试,将∠A 和∠B 剪下来,和 ∠C 拼在一起,发现拼成了一个平角,所以内角和是180°
根据目前的知识水平,我们要用说理的方法来证明该结论的正确性了。
(学生活动:动手拼图。)
二、探索新知
1、三角形内角和定理
求证:三角形三个内角和等于180°。
已知:如图,△ABC。
求证:∠A+∠B +∠C=180° 。
A E
1 2
B
C D
(先让学生自己试着证明,老师在给出规范引领)
证明:延长BC至D,过点
C作CE∥BA。
∴∠A=∠1 ∠B=∠2
∵∠1+∠2+ ∠ACB=180°
∴∠A+∠B +∠ACB=180°
结论:三角形的内角和是180°
2、 直角三角形两锐角互余。
提问:(1)一个三角形可以有两个直角吗?
(2)一个三角形可以有两个钝角角吗?
(3)一个三角形可以有两个锐角吗?
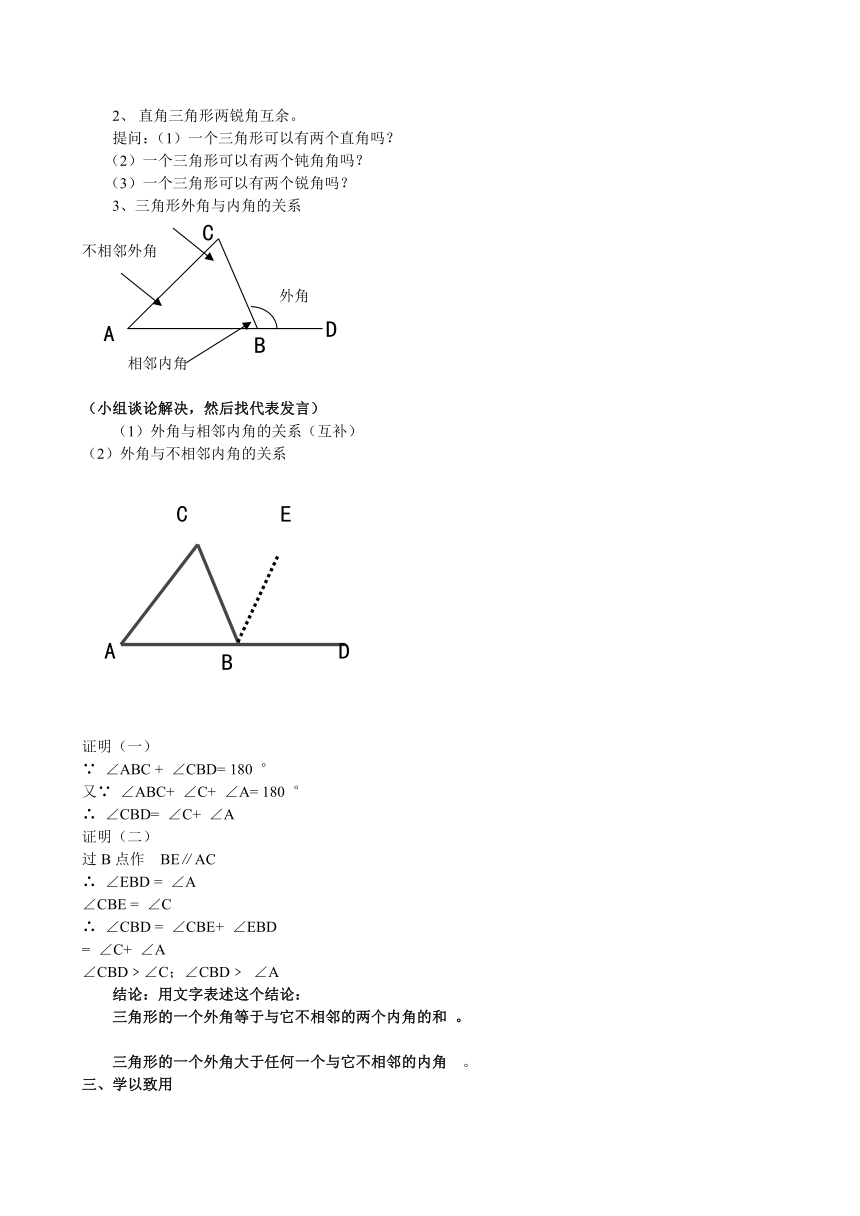
3、三角形外角与内角的关系
不相邻外角
外角
相邻内角
(小组谈论解决,然后找代表发言)
(1)外角与相邻内角的关系(互补)
(2)外角与不相邻内角的关系
证明(一)
∵ ∠ABC + ∠CBD= 180 °
又∵ ∠ABC+ ∠C+ ∠A= 180 °
∴ ∠CBD= ∠C+ ∠A
证明(二)
过B点作 BE∥AC
∴ ∠EBD = ∠A
∠CBE = ∠C
∴ ∠CBD = ∠CBE+ ∠EBD
= ∠C+ ∠A
∠CBD﹥∠C;∠CBD﹥ ∠A
结论:用文字表述这个结论:
三角形的一个外角等于与它不相邻的两个内角的和 。
三角形的一个外角大于任何一个与它不相邻的内角 。
三、学以致用
判断:1、三角形的一个外角等于两内角的和。 ( )
2、三角形的一个外角大于任何一个内角。( )
突出“不相邻”
(3)试一试计算角度
∠1= ∠1= ∠1=
∠1=_____;
∠2=_____;
∠3=______
(4)例题讲解:
例1 如图,D是△ABC的边BC上一点,∠B=∠BAD, ∠ADC=80 , ∠BAC=70 . 求:(1) ∠ B的度数;(2) ∠ C的度数。
A
B
D C
(学生思考后同桌可以交流思路,教师引导、点评,重点对∠ADC的认识:既可以看成三角形ADC的内角,也可以看成三角形ABD的外角。)。
引申:探索三角形的外角和
(1)三角形外角和是指在每个顶点处只取一个角共三个外角的和。
(2)动手操作,完成教材上的“做一做”让学生投影到白板上并做讲解。
结论:三角形的外角和是360°。
∠1+ ∠2+ ∠3= 360°
(3)练习:三角形的三个外角之比为2:3:4,则它的三个外角分别为( )
A. 80 120 160 B. 160 120 80
C. 100 60 20 D. 140 120 100 它的三个内角的比是多少?
四、反馈总结
让学生谈收获:
1. 三角形的外角性质:
三角形的一个外角等于与它不相邻的两个内角的和;
三角形的一个外角大于任何一个与它不相邻的内角。
2. 三角形的内角和等于180 ,直角三角形两锐角互余。三角形的外角和等于360
3. 在求角的度数时,常可利用三角形的内角和及外角的性质来找数量关系;涉及图形时,可先把已知条件尽可能的在图中标出来,有助于直观分析题意。
五、作业布置
C
D
B
A
C E
A
D
B
2
1
3
37°
155°
1
2
3
A
B
C
教学目标
知识与技能
1、理解三角形的内角和、外角和以及外角的性质。
2、学会用简单的说理来计算三角形相关的角。
过程与方法
经历三角形内角和、外角和及性质的探索过程,培养实践能力及观察总结能力。
情感态度与价值观
在学习过程中,激发学生主动学习数学的兴趣,体验数学学习成功的喜悦。
重点难点
重点:三角形内角和定理的证明,三角形外角和定理与性质。
难点:三角形内角和定理和外角性质的证明方法。
教学设计
一、情境引入
同学们,在小学咱们曾经学过三角形的内角和是吧,是怎样总结出来的呢?把三个角剪下来重新拼一拼的。请一个同学来试一试,将∠A 和∠B 剪下来,和 ∠C 拼在一起,发现拼成了一个平角,所以内角和是180°
根据目前的知识水平,我们要用说理的方法来证明该结论的正确性了。
(学生活动:动手拼图。)
二、探索新知
1、三角形内角和定理
求证:三角形三个内角和等于180°。
已知:如图,△ABC。
求证:∠A+∠B +∠C=180° 。
A E
1 2
B
C D
(先让学生自己试着证明,老师在给出规范引领)
证明:延长BC至D,过点
C作CE∥BA。
∴∠A=∠1 ∠B=∠2
∵∠1+∠2+ ∠ACB=180°
∴∠A+∠B +∠ACB=180°
结论:三角形的内角和是180°
2、 直角三角形两锐角互余。
提问:(1)一个三角形可以有两个直角吗?
(2)一个三角形可以有两个钝角角吗?
(3)一个三角形可以有两个锐角吗?
3、三角形外角与内角的关系
不相邻外角
外角
相邻内角
(小组谈论解决,然后找代表发言)
(1)外角与相邻内角的关系(互补)
(2)外角与不相邻内角的关系
证明(一)
∵ ∠ABC + ∠CBD= 180 °
又∵ ∠ABC+ ∠C+ ∠A= 180 °
∴ ∠CBD= ∠C+ ∠A
证明(二)
过B点作 BE∥AC
∴ ∠EBD = ∠A
∠CBE = ∠C
∴ ∠CBD = ∠CBE+ ∠EBD
= ∠C+ ∠A
∠CBD﹥∠C;∠CBD﹥ ∠A
结论:用文字表述这个结论:
三角形的一个外角等于与它不相邻的两个内角的和 。
三角形的一个外角大于任何一个与它不相邻的内角 。
三、学以致用
判断:1、三角形的一个外角等于两内角的和。 ( )
2、三角形的一个外角大于任何一个内角。( )
突出“不相邻”
(3)试一试计算角度
∠1= ∠1= ∠1=
∠1=_____;
∠2=_____;
∠3=______
(4)例题讲解:
例1 如图,D是△ABC的边BC上一点,∠B=∠BAD, ∠ADC=80 , ∠BAC=70 . 求:(1) ∠ B的度数;(2) ∠ C的度数。
A
B
D C
(学生思考后同桌可以交流思路,教师引导、点评,重点对∠ADC的认识:既可以看成三角形ADC的内角,也可以看成三角形ABD的外角。)。
引申:探索三角形的外角和
(1)三角形外角和是指在每个顶点处只取一个角共三个外角的和。
(2)动手操作,完成教材上的“做一做”让学生投影到白板上并做讲解。
结论:三角形的外角和是360°。
∠1+ ∠2+ ∠3= 360°
(3)练习:三角形的三个外角之比为2:3:4,则它的三个外角分别为( )
A. 80 120 160 B. 160 120 80
C. 100 60 20 D. 140 120 100 它的三个内角的比是多少?
四、反馈总结
让学生谈收获:
1. 三角形的外角性质:
三角形的一个外角等于与它不相邻的两个内角的和;
三角形的一个外角大于任何一个与它不相邻的内角。
2. 三角形的内角和等于180 ,直角三角形两锐角互余。三角形的外角和等于360
3. 在求角的度数时,常可利用三角形的内角和及外角的性质来找数量关系;涉及图形时,可先把已知条件尽可能的在图中标出来,有助于直观分析题意。
五、作业布置
C
D
B
A
C E
A
D
B
2
1
3
37°
155°
1
2
3
A
B
C
