华东师大版七年级数学下册 10.3.3旋转对称图形 教案
文档属性
| 名称 | 华东师大版七年级数学下册 10.3.3旋转对称图形 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 00:00:00 | ||
图片预览


文档简介
10.3.3旋转对称图形
华东师范大学出版社
本节课共1课时
一、教学设计:
1、教材分析:
旋转也是图形的一种基本变换,本节在学习了旋转的概念和特征之后,学生对于旋转的基本知识已经掌握,加上生活的经验,学生对于旋转对称图形有了初步的感知,为进一步学习打下基础,学习起来应该比较轻松.旋转角度的确定是本节课的难点,这里让学生经历“猜想、实验、探究、发现”的过程,自行归纳出公式,其次七年级的学生对于图形美的欣赏能力较弱,本节课最后让学生来设计旋转对称图形有意识地培养了学生这方面的能力.
2、课标分析
课程标准提出:在第三学段中,“学生将探索基本图形(直线形、圆)的基本性质及其相互关系,进一步丰富对空间图形的认识和感受,学习平移、旋转、对称的基本性质,欣赏并体验变换在现实生活中的广泛应用,学习运用坐标系确定物体位置的方法,发展空间观念”.在教学中,应注重所学内容与现 实生活的联系,注重使学生经历观察、操作、推理、想像等探索过程.
具体要求: ①通过具体实例认识旋转对称图形,探索它的基本特征,熟练判断旋转中心和旋转角度;②感受旋转对称图形的美,体会数学的图形美、对称美;③探索图形之间的变换关系;④灵活运用轴对称、平移和旋转的组合进行图案设计.
3、学情分析:
学生是晋江市一般中学的学生,地处城乡结合部,学生的动手能力较弱,但绝大部分学生学习数学的兴趣较浓,通过近一年来的学习指导,学生有一定的探究意识学生已经学了平移、轴对称、旋转等图形的变换,有较强的动手操作能力和一定的小组合作经验,对探究图形变换的规律和性质有一定的基础但解决实际问题的能力和创新意识还有待提高.
4、教学目标:
(1)知识与技能:
通过具体实例认识旋转对称图形;能判断一个图形是不是旋转对称图形;能确定旋转对称图形的旋转角及旋转中心.
(2)过程与方法:
学生在经历“猜想、实验、探究、发现、运用”的过程中,体验数学与生活密切联系,培养勤于思考,乐于探索的良好学习习惯以及有序,周密思考问题的思维品质.
(3)情感态度与价值观:
通过旋转对称图形和旋转对称的特征,利用旋转设计一些图案,增强学生学习几何的趣味感,培养审美情操,体验探索发现数学奥秘的成功愉悦,感悟数学的魅力,激发学生学习数学的兴趣.
5、教学重、难点
(1)教学重点:旋转对称图形的定义及旋转角的确定.
(2)教学难点:旋转角度的确定及设计旋转对称图形.
二、教学过程
(一)历史渊源,初步感知
课外阅读材料:
古建筑中的旋转对称——从敦煌洞窟到欧洲教堂.
敦煌的佛教洞窟与欧洲的基督教堂相距数千公里,文化和宗教背景截然不同,然而在相距几百年的时间里,却先后出现了完全相同的一种图案:三只兔子相互追逐形成一个环.
这几个图案有什么特点呢,三只兔子是如何中国传到欧洲的呢
(设计意图:将今天所学的内容和史实相互联系,可以激起学生的学习兴趣,丰富扩充学生的学习内容,也让学生对旋转对称图形有初步感受.)
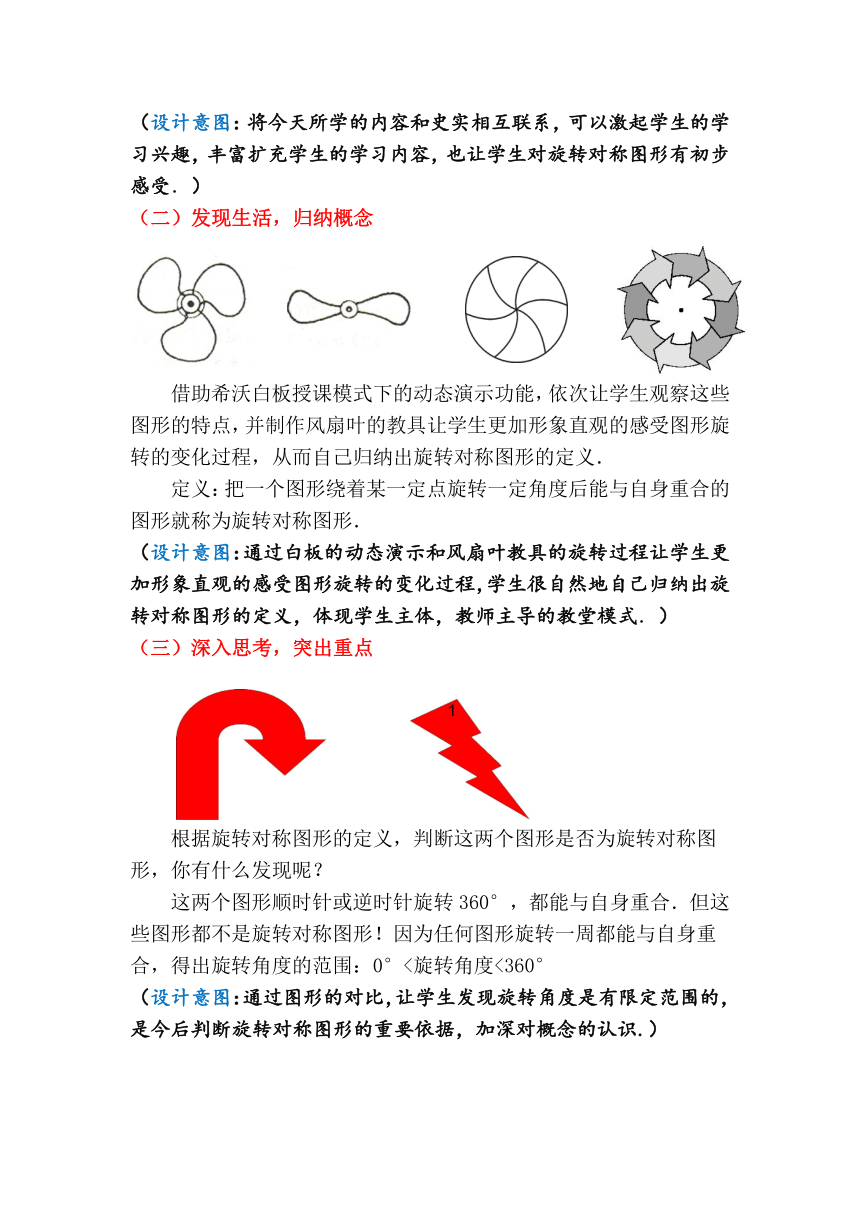
(二)发现生活,归纳概念
借助希沃白板授课模式下的动态演示功能,依次让学生观察这些图形的特点,并制作风扇叶的教具让学生更加形象直观的感受图形旋转的变化过程,从而自己归纳出旋转对称图形的定义.
定义:把一个图形绕着某一定点旋转一定角度后能与自身重合的图形就称为旋转对称图形.
(设计意图:通过白板的动态演示和风扇叶教具的旋转过程让学生更加形象直观的感受图形旋转的变化过程,学生很自然地自己归纳出旋转对称图形的定义,体现学生主体,教师主导的教堂模式.)
(三)深入思考,突出重点
根据旋转对称图形的定义,判断这两个图形是否为旋转对称图形,你有什么发现呢?
这两个图形顺时针或逆时针旋转360°,都能与自身重合.但这些图形都不是旋转对称图形!因为任何图形旋转一周都能与自身重合,得出旋转角度的范围:0°<旋转角度<360°
(设计意图:通过图形的对比,让学生发现旋转角度是有限定范围的,是今后判断旋转对称图形的重要依据,加深对概念的认识.)
(四)游戏比拼,巩固概念
1、举例有哪些字母或符号是旋转对称图形呢 (如S,H,%)
2、随机抽取两名学生进行游戏比拼,判断下列哪些字母和符号是旋转对称图形.
(设计意图:现学现用,活学活用,即时练习,在游戏中巩固加深旋转对称图形的定义.)
(五)探究新知,突破难点
探究下面这个图形:
1、 旋转中心在何处?(在图形的正中心)
2、 旋转角度有什么规律?
至少旋转 与自身重合,
或者旋转 、 也能与自身重合.
教师通过白板旋转演示让学生发现旋转角度与图形的基本图案个数的关系,即旋转角度最小是
(设计意图:教师通过白板旋转演示让学生发现旋转角度的特点,以及旋转角度与图形之间的联系,探究基本图案的个数和最小旋转角度的关系,让学生在观察分析中学习新知识,突破本节课的难点.)
(六)小试牛刀,寓学于乐
1、通过拖动选项这一游戏环节让学生回答以上图形的最小旋转角度,加深巩固求解旋转对称图形的旋转角度.
2、判断下面两个图形是否是旋转对称图形,若是,说出旋转角度.
(设计意图:设置拖动选项功能,及手动旋转图形让学生感受旋转过程,学生在游戏中学习,提高学习兴趣,又及时练习,新知得以巩固.)
(七)新旧联系,融会贯通
先让学生动手画出将△ABC经过两次翻拍后的△A”B”C”,画好后观察思考你有什么发现.
接着教师通过几何画板动态演示,并引导学生思考通过怎样的变换也能使△ABC变成△A”B”C”,由此学生很容易得出:两次轴对称等于一次的旋转对称.
(设计意图:通过动手操作、观察发现,几何画板动态直观感知,将前面学习的轴对称与本节旋转对称相联系,让学生对知识的整体性有更好的把握,融会贯通,拓展知识面.)
(八)多彩设计,展示分享
1、首尾呼应,课前我们展示的“三只兔子”的故事,你现在知道这三只兔子的秘密了吗?(三们组成了一个旋转对称图形.)
2、小小设计师:以小组为单位,请你设计一个旋转对称图形,并上台展示,说明它旋转几度能与自身重合.
教师循堂并将优秀设计作品上传至白板,之后请“设计师”们上台展示并讲解设计思路或说明该图形旋转几度能与自身重合.
(设计意图:首尾呼应,让学生再次感受旋转对称图形之美,与史实结合,更富神秘色彩,激发学生的探索精神;其次,本节课的最后一个环节让学生根据所学设计旋转对称图形,并让学生上台展示分享,既让学生动手操作,又激发了学生的创意和灵感,积极培养学生的数学核心素养—几何直观.展示环节锻炼了学生的解说及表达能力,本节课内容在此环节得以升华.)
(九)课堂小结,布置作业
1、课堂小结:
①什么是旋转对称图形;
②会找旋转中心和旋转度数;
③轴对称与旋转的关系.
2、作业:P124:第1~4题
三、课后反思
(另附文本)
华东师范大学出版社
本节课共1课时
一、教学设计:
1、教材分析:
旋转也是图形的一种基本变换,本节在学习了旋转的概念和特征之后,学生对于旋转的基本知识已经掌握,加上生活的经验,学生对于旋转对称图形有了初步的感知,为进一步学习打下基础,学习起来应该比较轻松.旋转角度的确定是本节课的难点,这里让学生经历“猜想、实验、探究、发现”的过程,自行归纳出公式,其次七年级的学生对于图形美的欣赏能力较弱,本节课最后让学生来设计旋转对称图形有意识地培养了学生这方面的能力.
2、课标分析
课程标准提出:在第三学段中,“学生将探索基本图形(直线形、圆)的基本性质及其相互关系,进一步丰富对空间图形的认识和感受,学习平移、旋转、对称的基本性质,欣赏并体验变换在现实生活中的广泛应用,学习运用坐标系确定物体位置的方法,发展空间观念”.在教学中,应注重所学内容与现 实生活的联系,注重使学生经历观察、操作、推理、想像等探索过程.
具体要求: ①通过具体实例认识旋转对称图形,探索它的基本特征,熟练判断旋转中心和旋转角度;②感受旋转对称图形的美,体会数学的图形美、对称美;③探索图形之间的变换关系;④灵活运用轴对称、平移和旋转的组合进行图案设计.
3、学情分析:
学生是晋江市一般中学的学生,地处城乡结合部,学生的动手能力较弱,但绝大部分学生学习数学的兴趣较浓,通过近一年来的学习指导,学生有一定的探究意识学生已经学了平移、轴对称、旋转等图形的变换,有较强的动手操作能力和一定的小组合作经验,对探究图形变换的规律和性质有一定的基础但解决实际问题的能力和创新意识还有待提高.
4、教学目标:
(1)知识与技能:
通过具体实例认识旋转对称图形;能判断一个图形是不是旋转对称图形;能确定旋转对称图形的旋转角及旋转中心.
(2)过程与方法:
学生在经历“猜想、实验、探究、发现、运用”的过程中,体验数学与生活密切联系,培养勤于思考,乐于探索的良好学习习惯以及有序,周密思考问题的思维品质.
(3)情感态度与价值观:
通过旋转对称图形和旋转对称的特征,利用旋转设计一些图案,增强学生学习几何的趣味感,培养审美情操,体验探索发现数学奥秘的成功愉悦,感悟数学的魅力,激发学生学习数学的兴趣.
5、教学重、难点
(1)教学重点:旋转对称图形的定义及旋转角的确定.
(2)教学难点:旋转角度的确定及设计旋转对称图形.
二、教学过程
(一)历史渊源,初步感知
课外阅读材料:
古建筑中的旋转对称——从敦煌洞窟到欧洲教堂.
敦煌的佛教洞窟与欧洲的基督教堂相距数千公里,文化和宗教背景截然不同,然而在相距几百年的时间里,却先后出现了完全相同的一种图案:三只兔子相互追逐形成一个环.
这几个图案有什么特点呢,三只兔子是如何中国传到欧洲的呢
(设计意图:将今天所学的内容和史实相互联系,可以激起学生的学习兴趣,丰富扩充学生的学习内容,也让学生对旋转对称图形有初步感受.)
(二)发现生活,归纳概念
借助希沃白板授课模式下的动态演示功能,依次让学生观察这些图形的特点,并制作风扇叶的教具让学生更加形象直观的感受图形旋转的变化过程,从而自己归纳出旋转对称图形的定义.
定义:把一个图形绕着某一定点旋转一定角度后能与自身重合的图形就称为旋转对称图形.
(设计意图:通过白板的动态演示和风扇叶教具的旋转过程让学生更加形象直观的感受图形旋转的变化过程,学生很自然地自己归纳出旋转对称图形的定义,体现学生主体,教师主导的教堂模式.)
(三)深入思考,突出重点
根据旋转对称图形的定义,判断这两个图形是否为旋转对称图形,你有什么发现呢?
这两个图形顺时针或逆时针旋转360°,都能与自身重合.但这些图形都不是旋转对称图形!因为任何图形旋转一周都能与自身重合,得出旋转角度的范围:0°<旋转角度<360°
(设计意图:通过图形的对比,让学生发现旋转角度是有限定范围的,是今后判断旋转对称图形的重要依据,加深对概念的认识.)
(四)游戏比拼,巩固概念
1、举例有哪些字母或符号是旋转对称图形呢 (如S,H,%)
2、随机抽取两名学生进行游戏比拼,判断下列哪些字母和符号是旋转对称图形.
(设计意图:现学现用,活学活用,即时练习,在游戏中巩固加深旋转对称图形的定义.)
(五)探究新知,突破难点
探究下面这个图形:
1、 旋转中心在何处?(在图形的正中心)
2、 旋转角度有什么规律?
至少旋转 与自身重合,
或者旋转 、 也能与自身重合.
教师通过白板旋转演示让学生发现旋转角度与图形的基本图案个数的关系,即旋转角度最小是
(设计意图:教师通过白板旋转演示让学生发现旋转角度的特点,以及旋转角度与图形之间的联系,探究基本图案的个数和最小旋转角度的关系,让学生在观察分析中学习新知识,突破本节课的难点.)
(六)小试牛刀,寓学于乐
1、通过拖动选项这一游戏环节让学生回答以上图形的最小旋转角度,加深巩固求解旋转对称图形的旋转角度.
2、判断下面两个图形是否是旋转对称图形,若是,说出旋转角度.
(设计意图:设置拖动选项功能,及手动旋转图形让学生感受旋转过程,学生在游戏中学习,提高学习兴趣,又及时练习,新知得以巩固.)
(七)新旧联系,融会贯通
先让学生动手画出将△ABC经过两次翻拍后的△A”B”C”,画好后观察思考你有什么发现.
接着教师通过几何画板动态演示,并引导学生思考通过怎样的变换也能使△ABC变成△A”B”C”,由此学生很容易得出:两次轴对称等于一次的旋转对称.
(设计意图:通过动手操作、观察发现,几何画板动态直观感知,将前面学习的轴对称与本节旋转对称相联系,让学生对知识的整体性有更好的把握,融会贯通,拓展知识面.)
(八)多彩设计,展示分享
1、首尾呼应,课前我们展示的“三只兔子”的故事,你现在知道这三只兔子的秘密了吗?(三们组成了一个旋转对称图形.)
2、小小设计师:以小组为单位,请你设计一个旋转对称图形,并上台展示,说明它旋转几度能与自身重合.
教师循堂并将优秀设计作品上传至白板,之后请“设计师”们上台展示并讲解设计思路或说明该图形旋转几度能与自身重合.
(设计意图:首尾呼应,让学生再次感受旋转对称图形之美,与史实结合,更富神秘色彩,激发学生的探索精神;其次,本节课的最后一个环节让学生根据所学设计旋转对称图形,并让学生上台展示分享,既让学生动手操作,又激发了学生的创意和灵感,积极培养学生的数学核心素养—几何直观.展示环节锻炼了学生的解说及表达能力,本节课内容在此环节得以升华.)
(九)课堂小结,布置作业
1、课堂小结:
①什么是旋转对称图形;
②会找旋转中心和旋转度数;
③轴对称与旋转的关系.
2、作业:P124:第1~4题
三、课后反思
(另附文本)
