吉安三中2012年下半年期中考试高一年级数学试卷
文档属性
| 名称 | 吉安三中2012年下半年期中考试高一年级数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 130.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-28 18:22:22 | ||
图片预览


文档简介
吉安三中2012年下半年期中考试高一年级数学试卷
(时间120分钟,满分150分) 命题人:黄晓阳
第Ⅰ卷
一、选择题:本大题共10题,每小题5分,共50分
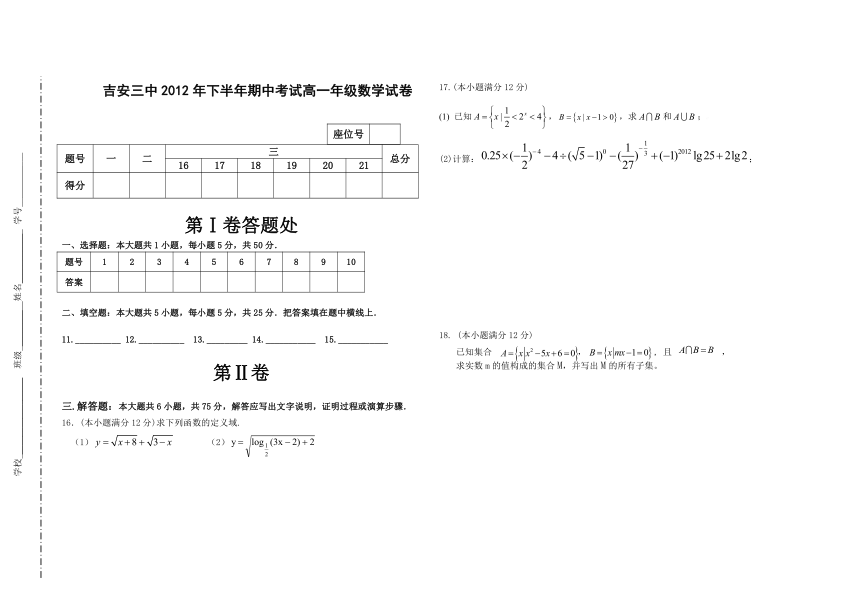
1.设集合,集合,,则等于( )
A.{ 5 } B. C. D.
2.已知集合, 那么集合为( )
A. B. C. D.
3.设全集,图中阴影部分所表示的集合是 ( )
A. B.
C. D.
4. 下列四个图像中,是函数图像的是 ( )
A. ① B. ①③④ C. ①②③ D. ③④
5. 已知,则等于 ( )
A. B. C. D.
6.如果函数对任意实数都有,那么( )
A.<< B.<<
C.<< D.<<
7. 如果函数在区间上是减少的,那么实数
的取值范围是 ( )
A B C D
8.某学生在校运动会参加3000米项目,匀速跑步前进一段路程后 ,因体力不足,减缓了跑步速度,并且坚持到达了终点,下图中横轴表示出发后的时间,纵轴表示该学生离到达终点还需要跑的路程,则较符合该学生跑法的图是( )
9.下列所给4个图象中,与所给3件事吻合最好的顺序是 ( )
①我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本过了一会儿再上学;
A B C D
9.直角梯形ABCD如图(1),动点P从B点出发,由B→C→D→A沿边运动,设点P运动的距离为x,ΔABP的面积为f(x).如果函数y= f(x)的图象如图(2),则ΔABC的面积为( )
A.10 B.16 C.18 D.32
10.国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4000元的按超过部分的14% 纳税;超过4000元的按全稿酬的11% 纳税.某人出版了一书共纳税420元,这个人的稿费为 ( )
A. 3800元 B. 5600元 C. 3818元 D. 3000元
二、填空题:本大题共5小题,每小题5分,共25分
11.如图,函数的图象是折线段,
其中的坐标分别为,
则 .
12.设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图,
则不等式f(x)<0的解集是________ .
13.设是A到B的一个映射,其中 A=B=,
,则在的作用下的原象是
14.函数的单调递增区间是 .
15.已知下列各组函数:
(1),;
(2),
(3),圆面积关于圆半径的函数;
(4),。
其中表示同一函数的是第 组.
吉安三中2012年下半年期中考试高一年级数学试卷
座位号
题号
一
二
三
总分
16
17
18
19
20
21
得分
第Ⅰ卷答题处
一、选择题:本大题共1小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上.
11.__________ 12.__________ 13._________ 14.___________ 15.___________
第Ⅱ卷
三.解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)求下列函数的定义域.
(1) (2)
17.(本小题满分12分)
(1) 已知,,求和;
(2)计算:;
18. (本小题满分12分)
已知集合 , , 且 ,
求实数m的值构成的集合M,并写出M的所有子集。
19.(本小题满分12分)
已知是R上的偶函数,时,
(1)当时,求的解析式.
(2)作出函数的图象,并指出其单调区间.
20. (本小题满分13分)
某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次, 如果每次拖7节车厢,则每日能来回10次.
(1)若每日来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式:
(2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。
21.(本小题满分14分)
已知定义域为的函数是奇函数.
(1)求的值;
(2)判断函数的单调性,并证明.
(3)若对任意的,不等式恒成立,求的取值范围.
吉安三中2012年下半年期中考试高一年级数学试卷答案
第Ⅰ卷答题处
一、选择题:本大题共1小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
D
B
B
A
A
D
B
A
二、填空题:本大题共5小题,每小题5分,共25分.
11. 2 ; 12. {x|-2<x<0或2<x≤5}; 13. ;14. [2,3); 15.(3)(4)
第Ⅱ卷
三.解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16.解:(1)∵ ………6分
∴定义域为
(2)(,2]------------ (6分)
17. 解:(1)A={x|-11} …………4分
={x|1-1} …………6分
(2)原式= …………4分
= 4-4-3+lg100
= -1 …………6分
18. 解:由条件可知,A={2,3} ……………2分
当m=0时, B= ? …………4分
当m≠0时, m=1∕2 或m=1∕3
得M={0,1∕2 ,1∕3} …………8分
M的所有子集:? ,{0},{1∕2 },{1∕3},{0,1∕2 }
{0,1∕3},{1∕2 ,1∕3},{0,1∕2 ,1∕3}…………12分
19.(1) 当X<0时, -X>0
则
得 …………4分
( 2) 图像 …………8分
单调递增区间:[-1,0],[1,+∞]
单调递减区间(- ∞,-1),(0,1) …………12分
20. 解:(1)设每日来回y次,每次挂x节车厢,由题意
当x=4时y=16 当x=7时y=10得下列方程组:
16=4k+b
10=7k+b ……4分
解得:k= b=24
……… 6分
(2)设每日来回y次,每次挂x节车厢由题意知,每日挂车厢最多时,营运人数最多,设每日营运S节车厢则
……10分
所以当时,此时y=12,
则每日最多运营人数为110×72=7920(人) ……12分
答:这列火车每天来回12次,才能使运营人数最多。每天最多运营人数为7920.
……13分
21.解:(1) ∵为上是奇函数,所以=0,即…….2分
(2)由(Ⅰ)知,
设则
因为函数y=2在R上是增函数且 ∴>0
又>0 ∴>0即
∴在上为减函数. ……………………8分
(3)因是奇函数,从而不等式:
等价于, ……………………..10分
因为减函数,由上式推得:.
即对一切有:, …………………………12分
从而判别式. ………………………14分
(时间120分钟,满分150分) 命题人:黄晓阳
第Ⅰ卷
一、选择题:本大题共10题,每小题5分,共50分
1.设集合,集合,,则等于( )
A.{ 5 } B. C. D.
2.已知集合, 那么集合为( )
A. B. C. D.
3.设全集,图中阴影部分所表示的集合是 ( )
A. B.
C. D.
4. 下列四个图像中,是函数图像的是 ( )
A. ① B. ①③④ C. ①②③ D. ③④
5. 已知,则等于 ( )
A. B. C. D.
6.如果函数对任意实数都有,那么( )
A.<< B.<<
C.<< D.<<
7. 如果函数在区间上是减少的,那么实数
的取值范围是 ( )
A B C D
8.某学生在校运动会参加3000米项目,匀速跑步前进一段路程后 ,因体力不足,减缓了跑步速度,并且坚持到达了终点,下图中横轴表示出发后的时间,纵轴表示该学生离到达终点还需要跑的路程,则较符合该学生跑法的图是( )
9.下列所给4个图象中,与所给3件事吻合最好的顺序是 ( )
①我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本过了一会儿再上学;
A B C D
9.直角梯形ABCD如图(1),动点P从B点出发,由B→C→D→A沿边运动,设点P运动的距离为x,ΔABP的面积为f(x).如果函数y= f(x)的图象如图(2),则ΔABC的面积为( )
A.10 B.16 C.18 D.32
10.国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4000元的按超过部分的14% 纳税;超过4000元的按全稿酬的11% 纳税.某人出版了一书共纳税420元,这个人的稿费为 ( )
A. 3800元 B. 5600元 C. 3818元 D. 3000元
二、填空题:本大题共5小题,每小题5分,共25分
11.如图,函数的图象是折线段,
其中的坐标分别为,
则 .
12.设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图,
则不等式f(x)<0的解集是________ .
13.设是A到B的一个映射,其中 A=B=,
,则在的作用下的原象是
14.函数的单调递增区间是 .
15.已知下列各组函数:
(1),;
(2),
(3),圆面积关于圆半径的函数;
(4),。
其中表示同一函数的是第 组.
吉安三中2012年下半年期中考试高一年级数学试卷
座位号
题号
一
二
三
总分
16
17
18
19
20
21
得分
第Ⅰ卷答题处
一、选择题:本大题共1小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上.
11.__________ 12.__________ 13._________ 14.___________ 15.___________
第Ⅱ卷
三.解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)求下列函数的定义域.
(1) (2)
17.(本小题满分12分)
(1) 已知,,求和;
(2)计算:;
18. (本小题满分12分)
已知集合 , , 且 ,
求实数m的值构成的集合M,并写出M的所有子集。
19.(本小题满分12分)
已知是R上的偶函数,时,
(1)当时,求的解析式.
(2)作出函数的图象,并指出其单调区间.
20. (本小题满分13分)
某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次, 如果每次拖7节车厢,则每日能来回10次.
(1)若每日来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式:
(2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。
21.(本小题满分14分)
已知定义域为的函数是奇函数.
(1)求的值;
(2)判断函数的单调性,并证明.
(3)若对任意的,不等式恒成立,求的取值范围.
吉安三中2012年下半年期中考试高一年级数学试卷答案
第Ⅰ卷答题处
一、选择题:本大题共1小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
D
B
B
A
A
D
B
A
二、填空题:本大题共5小题,每小题5分,共25分.
11. 2 ; 12. {x|-2<x<0或2<x≤5}; 13. ;14. [2,3); 15.(3)(4)
第Ⅱ卷
三.解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16.解:(1)∵ ………6分
∴定义域为
(2)(,2]------------ (6分)
17. 解:(1)A={x|-1
={x|1
(2)原式= …………4分
= 4-4-3+lg100
= -1 …………6分
18. 解:由条件可知,A={2,3} ……………2分
当m=0时, B= ? …………4分
当m≠0时, m=1∕2 或m=1∕3
得M={0,1∕2 ,1∕3} …………8分
M的所有子集:? ,{0},{1∕2 },{1∕3},{0,1∕2 }
{0,1∕3},{1∕2 ,1∕3},{0,1∕2 ,1∕3}…………12分
19.(1) 当X<0时, -X>0
则
得 …………4分
( 2) 图像 …………8分
单调递增区间:[-1,0],[1,+∞]
单调递减区间(- ∞,-1),(0,1) …………12分
20. 解:(1)设每日来回y次,每次挂x节车厢,由题意
当x=4时y=16 当x=7时y=10得下列方程组:
16=4k+b
10=7k+b ……4分
解得:k= b=24
……… 6分
(2)设每日来回y次,每次挂x节车厢由题意知,每日挂车厢最多时,营运人数最多,设每日营运S节车厢则
……10分
所以当时,此时y=12,
则每日最多运营人数为110×72=7920(人) ……12分
答:这列火车每天来回12次,才能使运营人数最多。每天最多运营人数为7920.
……13分
21.解:(1) ∵为上是奇函数,所以=0,即…….2分
(2)由(Ⅰ)知,
设则
因为函数y=2在R上是增函数且 ∴>0
又>0 ∴>0即
∴在上为减函数. ……………………8分
(3)因是奇函数,从而不等式:
等价于, ……………………..10分
因为减函数,由上式推得:.
即对一切有:, …………………………12分
从而判别式. ………………………14分
同课章节目录
