人教版七年级下册8.4 三元一次方程组的解法 课件(共17张)
文档属性
| 名称 | 人教版七年级下册8.4 三元一次方程组的解法 课件(共17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 508.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 09:48:07 | ||
图片预览





文档简介
(共17张PPT)
人教版数学七年级下册
第八章 二元一次方程组
8.4 三元一次方程组的解法
学习目标
1.了解三元一次方程组的概念。
2.会解简单的三元一次方程组。
3.会借助三元一次方程组解决简单的问题。
公元5世纪末,我国古代数学家张丘建在它所撰定的《算经》中,提出这样一个问题:“鸡翁一,值钱五;鸡母一,值钱三,鸡雏三,值钱一,百钱买百鸡,问鸡翁、母、雏各几何?”意思是说公鸡每只5元,母鸡每只3元,小鸡3只1元,用100元钱买100只鸡,求公鸡、母鸡、小鸡的只数。
探究
小明手头有12张面额分别为1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍,求1元、2元、5元纸币各多张?
解:设1元、2元、5元纸币分别为x张、y张、z张,由题意得
{
x+y+z=12
x+2y+5z=12
x=4y
探究
小明手头有12张面额分别为1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍,求1元、2元、5元纸币各多张?
解:设1元、2元、5元纸币分别为x张、y张、z张,由题意得
{
x+y+z=12
x+2y+5z=12
x=4y
1.三元一次方程组
方程组含有三个未知数,每个方程中含有未知数的项的次数都是一次,并且一共有三个方程,这样的方程组叫做三元一次方程组.
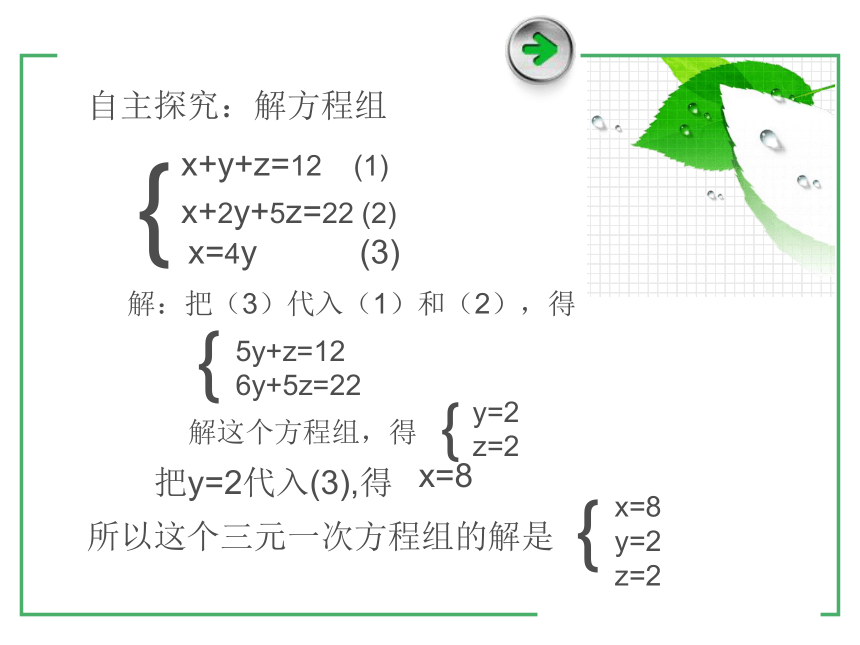
自主探究:解方程组
{
x+y+z=12 (1)
x+2y+5z=22 (2)
x=4y (3)
解:把(3)代入(1)和(2),得
{
5y+z=12
6y+5z=22
解这个方程组,得
{
y=2
z=2
把y=2代入(3),得
x=8
所以这个三元一次方程组的解是
{
x=8
y=2
z=2
解三元一次方程组的方法
陶中学数学组
基本思想:消元,即通过“代入”或“加减”进行消元,转化为二元一次方程组,进而转化为一元一次方程来解决。
三元一次方程组
二元一次方程组
一元一次方程
习题1、解方程组:
解: 将(1)代入(2),解得
将(1)代入(3)中,解得
所以,原方程组的解是
例1 解方程组:
解:(1)-(2)得
(4)
(3)+(4)得
解得:
把 代入(1)解得:
把 代入(3)解得:
所以,原方程组的解是:
例1 解方程组:
解:(1)+(2)+(3)得
所以,原方程组的解是:
2(x+y+z)=-2
即 x+y+z=-1 (4)
(4)-(1),得z=13
(4)-(2),得x=6
(4)-(3),得y=-20
当三元一次方程组有一个方程是二元一次方程时,就利用另两个方程用消去这二元一次方程所缺的那个元,与它组成二元一次方程组,再解此二元一次方程组,最后求得三元一次方程组的解。
结论
例题2 解方程组:
解:(1)+(2)得:
即
(4)
(2)+(3)得:
(5)
(4)×5-(5)得:
解得
,
把 代入(4),解得
把 、代入(1)中得:
所以,原方程组的解是
例题3
我校体育部的篮球个数比排球个数的2倍少3,足球个数与排球的比是2:3,三种球共有41个,则篮球、排球、足球三种球各有多少个?
解:设篮球有x个,排球有y个,足球有z个,得
{
x=2y-3
2y=3z
x+y+z=41
解得
{
x=21
y=12
z=8
答:篮球21个,排球12个,足球8个。
公元5世纪末,我国古代数学家张丘建在它所撰定的《算经》中,提出这样一个问题:“鸡翁一,值钱五;鸡母一,值钱三,鸡雏三,值钱一,百钱买百鸡,问鸡翁、母、雏各几何?”意思是说公鸡每只5元,母鸡每只3元,小鸡3只1元,用100元钱买100只鸡,求公鸡、母鸡、小鸡的只数。
拓展探究
小 结
1.三元一次方程组的概念
3.利用三元一次方程组解应用题
2.解三元一次方程组.
作业:
数学练习册47页做完
人教版数学七年级下册
第八章 二元一次方程组
8.4 三元一次方程组的解法
学习目标
1.了解三元一次方程组的概念。
2.会解简单的三元一次方程组。
3.会借助三元一次方程组解决简单的问题。
公元5世纪末,我国古代数学家张丘建在它所撰定的《算经》中,提出这样一个问题:“鸡翁一,值钱五;鸡母一,值钱三,鸡雏三,值钱一,百钱买百鸡,问鸡翁、母、雏各几何?”意思是说公鸡每只5元,母鸡每只3元,小鸡3只1元,用100元钱买100只鸡,求公鸡、母鸡、小鸡的只数。
探究
小明手头有12张面额分别为1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍,求1元、2元、5元纸币各多张?
解:设1元、2元、5元纸币分别为x张、y张、z张,由题意得
{
x+y+z=12
x+2y+5z=12
x=4y
探究
小明手头有12张面额分别为1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍,求1元、2元、5元纸币各多张?
解:设1元、2元、5元纸币分别为x张、y张、z张,由题意得
{
x+y+z=12
x+2y+5z=12
x=4y
1.三元一次方程组
方程组含有三个未知数,每个方程中含有未知数的项的次数都是一次,并且一共有三个方程,这样的方程组叫做三元一次方程组.
自主探究:解方程组
{
x+y+z=12 (1)
x+2y+5z=22 (2)
x=4y (3)
解:把(3)代入(1)和(2),得
{
5y+z=12
6y+5z=22
解这个方程组,得
{
y=2
z=2
把y=2代入(3),得
x=8
所以这个三元一次方程组的解是
{
x=8
y=2
z=2
解三元一次方程组的方法
陶中学数学组
基本思想:消元,即通过“代入”或“加减”进行消元,转化为二元一次方程组,进而转化为一元一次方程来解决。
三元一次方程组
二元一次方程组
一元一次方程
习题1、解方程组:
解: 将(1)代入(2),解得
将(1)代入(3)中,解得
所以,原方程组的解是
例1 解方程组:
解:(1)-(2)得
(4)
(3)+(4)得
解得:
把 代入(1)解得:
把 代入(3)解得:
所以,原方程组的解是:
例1 解方程组:
解:(1)+(2)+(3)得
所以,原方程组的解是:
2(x+y+z)=-2
即 x+y+z=-1 (4)
(4)-(1),得z=13
(4)-(2),得x=6
(4)-(3),得y=-20
当三元一次方程组有一个方程是二元一次方程时,就利用另两个方程用消去这二元一次方程所缺的那个元,与它组成二元一次方程组,再解此二元一次方程组,最后求得三元一次方程组的解。
结论
例题2 解方程组:
解:(1)+(2)得:
即
(4)
(2)+(3)得:
(5)
(4)×5-(5)得:
解得
,
把 代入(4),解得
把 、代入(1)中得:
所以,原方程组的解是
例题3
我校体育部的篮球个数比排球个数的2倍少3,足球个数与排球的比是2:3,三种球共有41个,则篮球、排球、足球三种球各有多少个?
解:设篮球有x个,排球有y个,足球有z个,得
{
x=2y-3
2y=3z
x+y+z=41
解得
{
x=21
y=12
z=8
答:篮球21个,排球12个,足球8个。
公元5世纪末,我国古代数学家张丘建在它所撰定的《算经》中,提出这样一个问题:“鸡翁一,值钱五;鸡母一,值钱三,鸡雏三,值钱一,百钱买百鸡,问鸡翁、母、雏各几何?”意思是说公鸡每只5元,母鸡每只3元,小鸡3只1元,用100元钱买100只鸡,求公鸡、母鸡、小鸡的只数。
拓展探究
小 结
1.三元一次方程组的概念
3.利用三元一次方程组解应用题
2.解三元一次方程组.
作业:
数学练习册47页做完
