人教版数学七下9.1.1不等式及其解集 课件(共23张)
文档属性
| 名称 | 人教版数学七下9.1.1不等式及其解集 课件(共23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 15:23:27 | ||
图片预览







文档简介
(共23张PPT)
人教版 七年级下册
9.1.1不等式及其解集
【教学目标】
1.了解不等式概念,理解不等式的解和解集。
2.培养数感,渗透数形结合的思想。
3.培养自主学习的能力,合作交流意识与探究精
神。
【教学重难点】
重点:不等式的解和解集的区别
难点:理解不等式的解集
拔河时力气的大小
从上面的图片中让我们感受到生活中的问题:身高、体重、速度等等,仅仅学习研究等量关系还远远不够,还需学习和研究不等关系。
现实生活中“不相等”处处可见。从今天起,我们开始学习一类新的数学知识:不等式。
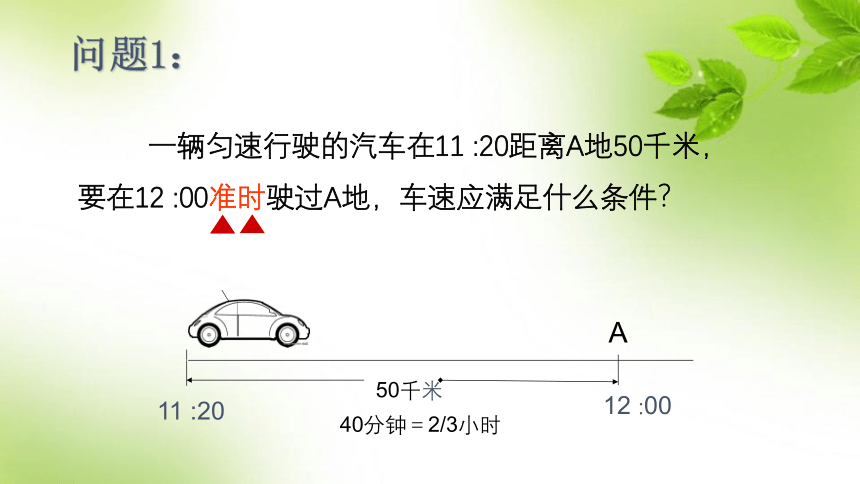
一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00准时驶过A地,车速应满足什么条件?
A
50千米
问题1:
11 :20
12 :00
40分钟=2/3小时
分析:
解:设车速是千米/时,根据题意,得
解得
所以汽车要在12:00准时驶过A
地,车速必须等于75千米/时
一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00之前驶过A地,车速应满足什么条件?
A
50千米
问题2:
11 :20
12 :00
40分钟=2/3小时
分析:
解:设车速是千米/时,根据题意,
在规定时间内路程必须得大于50
或者行使时间小于,
观察所得到的式子,它们之间有何区别?
思考:
像这样用等号连接表示相等关系的式子叫等式。
像这样用不等号连接表示不等关系的式子叫不等式。
②
①
1.不等式
像 和 那样,用不等号“<”或“>”表示不等关系的式子,叫做不等式。
注意:
① 用“≠”表示不等关系的式子也是不等式.
②“<” 、“>” 、“≠”、“ ≤”、“ ≥”都是不等号
③不等式中可以含有未知数,也可以不含有未知数.
①
②
练习巩固 马上过招:
第一招:判断下列式子哪些是不等式,哪
些不是?
(1) -8 <0 (2) 3-2
(3) 3+9=0 (4) 5+3> 420
(5)+3≠0 (6) 5-≥1
不等式可含有未知数,也可以无未知数
第二招:用不等式表示
(1)是正数
(2)与的和不小于5
(3)与2的差大于-1
(4)的4倍大于7
(5)一半小于3
(6)与1的差是非负数
(7)不大于2.
注意:不小于等同于大于或等于
注意:不大于等同于小于或等于
下面给出的数中,能使不等式>45成立吗?你还能找出其他的数吗?
20, 40, 50, 100.
当=20,20<45, 不成立;
当=40,40<45, 不成立;
当=50,50, 成立;
当=100,100>45, 成立.
解
不等式的解与解集
三
我们曾经学过“使方程两边相等的未知数的值就是方程的解”,与方程类似 , 能使不等式成立的未知数的值叫不等式的解.
代入法是检验某个值是否是不等式的解的简单、实用的方法.
例如:100是>45的解.
不等式的解与解集
三
一般的,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
想一想:
1.不等式的解和不等式的解集是一样的吗
2.不等式的解与解不等式一样吗?
求不等式的解集的过程叫解不等式.
不等式的解与解集
三
1、下列说法正确的是( )
A. x=3是2x+1>5的解
B. x=3是2x+1>5的唯一解
C. x=3不是2x+1>5的解
D. x=3是2x+1>5的解集
A
练一练
2、下列数值哪些是不等式+3>6的解?哪些不是?
-4,0,1,2.5,3,3.2,4.8,8
3、不等式2>8的解集是( )
A、>6 B、>16
C、>10 D、<1
×
√
×
×
×
×
√
√
C
补充题: 不等式<5有多少个解?有多少个正
整数解?
变式练习:不等式有多少个解?有多
少个非正整数解?
四、课堂小结
1、通过本节课学习你学到了哪些知识?
2、想提醒你的同学们注意什么事项?
布置作业:
必做题:小练习册P49第1--8题
选做题:小练习册P50第9题
人教版 七年级下册
9.1.1不等式及其解集
【教学目标】
1.了解不等式概念,理解不等式的解和解集。
2.培养数感,渗透数形结合的思想。
3.培养自主学习的能力,合作交流意识与探究精
神。
【教学重难点】
重点:不等式的解和解集的区别
难点:理解不等式的解集
拔河时力气的大小
从上面的图片中让我们感受到生活中的问题:身高、体重、速度等等,仅仅学习研究等量关系还远远不够,还需学习和研究不等关系。
现实生活中“不相等”处处可见。从今天起,我们开始学习一类新的数学知识:不等式。
一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00准时驶过A地,车速应满足什么条件?
A
50千米
问题1:
11 :20
12 :00
40分钟=2/3小时
分析:
解:设车速是千米/时,根据题意,得
解得
所以汽车要在12:00准时驶过A
地,车速必须等于75千米/时
一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00之前驶过A地,车速应满足什么条件?
A
50千米
问题2:
11 :20
12 :00
40分钟=2/3小时
分析:
解:设车速是千米/时,根据题意,
在规定时间内路程必须得大于50
或者行使时间小于,
观察所得到的式子,它们之间有何区别?
思考:
像这样用等号连接表示相等关系的式子叫等式。
像这样用不等号连接表示不等关系的式子叫不等式。
②
①
1.不等式
像 和 那样,用不等号“<”或“>”表示不等关系的式子,叫做不等式。
注意:
① 用“≠”表示不等关系的式子也是不等式.
②“<” 、“>” 、“≠”、“ ≤”、“ ≥”都是不等号
③不等式中可以含有未知数,也可以不含有未知数.
①
②
练习巩固 马上过招:
第一招:判断下列式子哪些是不等式,哪
些不是?
(1) -8 <0 (2) 3-2
(3) 3+9=0 (4) 5+3> 420
(5)+3≠0 (6) 5-≥1
不等式可含有未知数,也可以无未知数
第二招:用不等式表示
(1)是正数
(2)与的和不小于5
(3)与2的差大于-1
(4)的4倍大于7
(5)一半小于3
(6)与1的差是非负数
(7)不大于2.
注意:不小于等同于大于或等于
注意:不大于等同于小于或等于
下面给出的数中,能使不等式>45成立吗?你还能找出其他的数吗?
20, 40, 50, 100.
当=20,20<45, 不成立;
当=40,40<45, 不成立;
当=50,50, 成立;
当=100,100>45, 成立.
解
不等式的解与解集
三
我们曾经学过“使方程两边相等的未知数的值就是方程的解”,与方程类似 , 能使不等式成立的未知数的值叫不等式的解.
代入法是检验某个值是否是不等式的解的简单、实用的方法.
例如:100是>45的解.
不等式的解与解集
三
一般的,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
想一想:
1.不等式的解和不等式的解集是一样的吗
2.不等式的解与解不等式一样吗?
求不等式的解集的过程叫解不等式.
不等式的解与解集
三
1、下列说法正确的是( )
A. x=3是2x+1>5的解
B. x=3是2x+1>5的唯一解
C. x=3不是2x+1>5的解
D. x=3是2x+1>5的解集
A
练一练
2、下列数值哪些是不等式+3>6的解?哪些不是?
-4,0,1,2.5,3,3.2,4.8,8
3、不等式2>8的解集是( )
A、>6 B、>16
C、>10 D、<1
×
√
×
×
×
×
√
√
C
补充题: 不等式<5有多少个解?有多少个正
整数解?
变式练习:不等式有多少个解?有多
少个非正整数解?
四、课堂小结
1、通过本节课学习你学到了哪些知识?
2、想提醒你的同学们注意什么事项?
布置作业:
必做题:小练习册P49第1--8题
选做题:小练习册P50第9题
