人教版数学七下9.1.2不等式的性质 课件(共19张)
文档属性
| 名称 | 人教版数学七下9.1.2不等式的性质 课件(共19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 269.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
9.1.2 不等式的性质
1、观察下面这几个式子,完成下面的填空。
回忆思考
∵
∴
∴
同一个数
式子
等式的两边加(或减) 或 ,结果仍相等。
等式的性质1:
3
(x2+2y)
2、继续观察下面这几个式子,完成下面的填空。
回忆思考
∵
∴
∴
同一个数
等式的两边乘以(或除以) (除数不能为零),结果仍相等。
等式的性质2:
那么不等式有没有类似的性质呢?
3b
+
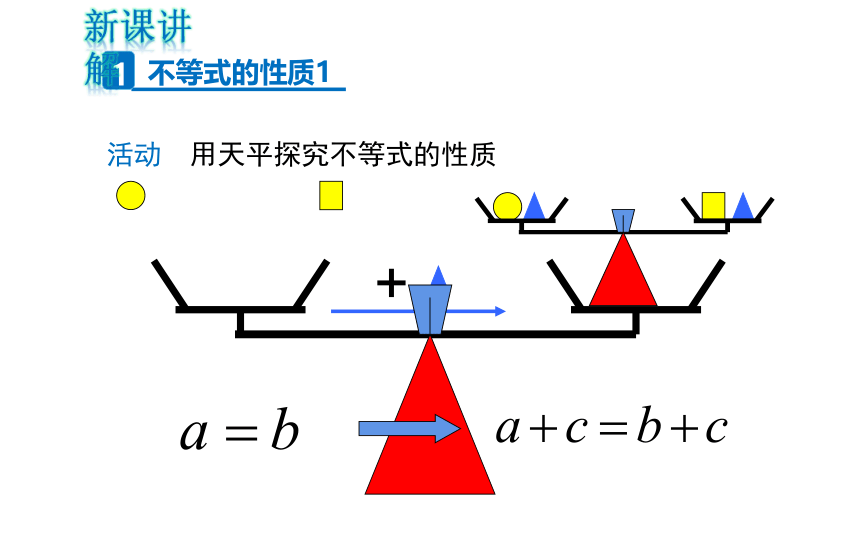
不等式的性质1
活动 用天平探究不等式的性质
1
新课讲解
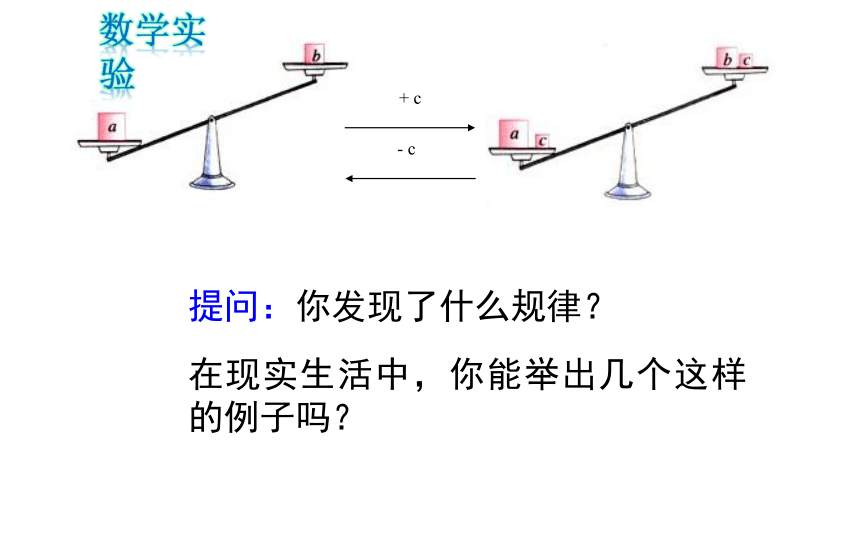
提问:你发现了什么规律?
在现实生活中,你能举出几个这样的例子吗?
+ c
- c
数学实验
不等式性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
新课讲解
字母表示为:
如果a>b,那么a±c > b±c
解: 因为 a>b,两边都加上8,
解: 因为 a由不等式性质1,得
a+8 > b+8;
由不等式性质1,得
a-6 < b-6 .
(1)已知 a>b,则a+8 b+8
(2)已知 a>
<
用“>”或“<”填空:
例题讲解
例1
练习1:用“>”或“<”填空,并说明是根据不等式的哪一条性质:
(1)若x+2>9,则x______7,
根据______________;
(2)若a-6<2,则a______8,
根据____________.
>
<
不等式性质1
不等式性质1
巩固练习
数学实验
提问:你又发现了什么规律?
在现实生活中,请你再举出几个这样的例子?
不等式性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
如果a > b,c > 0,那么 ac > bc , > .
新课讲解
字母表示为:
因为 a>b,两边都乘3,
因为 a解:
由不等式基本性质2,得
3a >3b.
由不等式基本性质2,得
5a < 5b.
(1)已知 a>b,则3a 3b ;
(2)已知 a>
<
用“>”或“<”填空:
例题讲解
解:
例2
因为 a>b,两边都除以3,
由不等式基本性质2,得
由不等式基本性质1,得
(3)已知 a>b,则 .
>
因为 ,两边都加上5,
例题讲解
解:
1.设a>b,用“<”“>”填空并回答是根据不等
式的哪一条基本性质.
(1) a - 7____b - 7;
(2) a÷6____b÷6
(3) 0.1a____0.1b;
(4) 8a___8b
(5) 2a+3____2b+3;
(6)(m2+1)a____ (m2+1)b(m为常数)
>
>
>
>
>
>
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质2
不等式的性质1,2
不等式的性质2
巩固练习
2.判断正误,并说明理由
(1)已知a+m>b+m,可得a>b
(2)已知4a>4b,可得a(3)已知2a+4>2b+4,可得a>b
(4)已知a>b,可得ac2>bc2
(√ )
(× )
(√ )
(× )
巩固练习
2.如果不等式 (a+1)x<a+1可变形为 x<1,那么a 必须满足________.
方法总结:当不等式的两边乘(或除以)同一个正数时,不等号的方向不变.
解析:根据不等式的基本性质可判断,a+1为正数,即a+1>0,可得 a>-1.
a>-1
拓展延伸
1.如果不等式ax<a,且x<1,那么a_____0
>
不等式的基本性质
不等式基本性质2
→
如果 那么
不等式的基本性质1
如果a>b,那么a+c>b+c,
a-c>b-c
→
课堂小结
比较等式与不等式的性质.
等式的性质1 不等式的性质1
等式的性质2 不等式的性质2
等式两边加(或减)同一个数(或式子),结果仍相等。
等式两边乘同一个数,或除以同一个不为零的数,结果仍相等。
不等式的两边加(或减)同一个数(或式子),不等号的方向不变。
不等式的两边乘(或除以)同一个正数,不等号的方向不变。
1.A层同学大册73页轻松尝试和74页能力提升1-7题。
2.B层同学大册73页轻松尝试和74页第6和7题。
3.C层同学大练73页做完。
作业布置
思考 等式有对称性及传递性,那么不等式具有对
称性和传递性吗
已知x>7,那么7由5如:5<11,11<15 ,5 15.
x>7 7<
性质(对称性):如果a>b,那么b性质(同向传递性):如果a>b,b>c,那么a>c.
拓展延伸
9.1.2 不等式的性质
1、观察下面这几个式子,完成下面的填空。
回忆思考
∵
∴
∴
同一个数
式子
等式的两边加(或减) 或 ,结果仍相等。
等式的性质1:
3
(x2+2y)
2、继续观察下面这几个式子,完成下面的填空。
回忆思考
∵
∴
∴
同一个数
等式的两边乘以(或除以) (除数不能为零),结果仍相等。
等式的性质2:
那么不等式有没有类似的性质呢?
3b
+
不等式的性质1
活动 用天平探究不等式的性质
1
新课讲解
提问:你发现了什么规律?
在现实生活中,你能举出几个这样的例子吗?
+ c
- c
数学实验
不等式性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
新课讲解
字母表示为:
如果a>b,那么a±c > b±c
解: 因为 a>b,两边都加上8,
解: 因为 a
a+8 > b+8;
由不等式性质1,得
a-6 < b-6 .
(1)已知 a>b,则a+8 b+8
(2)已知 a
<
用“>”或“<”填空:
例题讲解
例1
练习1:用“>”或“<”填空,并说明是根据不等式的哪一条性质:
(1)若x+2>9,则x______7,
根据______________;
(2)若a-6<2,则a______8,
根据____________.
>
<
不等式性质1
不等式性质1
巩固练习
数学实验
提问:你又发现了什么规律?
在现实生活中,请你再举出几个这样的例子?
不等式性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
如果a > b,c > 0,那么 ac > bc , > .
新课讲解
字母表示为:
因为 a>b,两边都乘3,
因为 a
由不等式基本性质2,得
3a >3b.
由不等式基本性质2,得
5a < 5b.
(1)已知 a>b,则3a 3b ;
(2)已知 a
<
用“>”或“<”填空:
例题讲解
解:
例2
因为 a>b,两边都除以3,
由不等式基本性质2,得
由不等式基本性质1,得
(3)已知 a>b,则 .
>
因为 ,两边都加上5,
例题讲解
解:
1.设a>b,用“<”“>”填空并回答是根据不等
式的哪一条基本性质.
(1) a - 7____b - 7;
(2) a÷6____b÷6
(3) 0.1a____0.1b;
(4) 8a___8b
(5) 2a+3____2b+3;
(6)(m2+1)a____ (m2+1)b(m为常数)
>
>
>
>
>
>
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质2
不等式的性质1,2
不等式的性质2
巩固练习
2.判断正误,并说明理由
(1)已知a+m>b+m,可得a>b
(2)已知4a>4b,可得a
(4)已知a>b,可得ac2>bc2
(√ )
(× )
(√ )
(× )
巩固练习
2.如果不等式 (a+1)x<a+1可变形为 x<1,那么a 必须满足________.
方法总结:当不等式的两边乘(或除以)同一个正数时,不等号的方向不变.
解析:根据不等式的基本性质可判断,a+1为正数,即a+1>0,可得 a>-1.
a>-1
拓展延伸
1.如果不等式ax<a,且x<1,那么a_____0
>
不等式的基本性质
不等式基本性质2
→
如果 那么
不等式的基本性质1
如果a>b,那么a+c>b+c,
a-c>b-c
→
课堂小结
比较等式与不等式的性质.
等式的性质1 不等式的性质1
等式的性质2 不等式的性质2
等式两边加(或减)同一个数(或式子),结果仍相等。
等式两边乘同一个数,或除以同一个不为零的数,结果仍相等。
不等式的两边加(或减)同一个数(或式子),不等号的方向不变。
不等式的两边乘(或除以)同一个正数,不等号的方向不变。
1.A层同学大册73页轻松尝试和74页能力提升1-7题。
2.B层同学大册73页轻松尝试和74页第6和7题。
3.C层同学大练73页做完。
作业布置
思考 等式有对称性及传递性,那么不等式具有对
称性和传递性吗
已知x>7,那么7
x>7 7
性质(对称性):如果a>b,那么b
拓展延伸
