人教版数学七下9.1.2不等式的性质 课件(共16张)
文档属性
| 名称 | 人教版数学七下9.1.2不等式的性质 课件(共16张) |  | |
| 格式 | pptx | ||
| 文件大小 | 271.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 20:11:23 | ||
图片预览






文档简介
(共16张PPT)
9.1.2 不等式的性质
交流预习
四星小组交流预习作业中存在的问题
(2分钟)
要求:B.C.D星把预习作业中的每一个问题先与A星交流,
A星及时指点。
举例说明你是怎样推导出不等式性质的?
互助探究一
正数
不变
负数
改变
不等式的性质2:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
不等式的性质3:不等式的两边都乘以(或除以)同一个_______,不等号的方向______。
如果a>b,那么a±c b±c。
不等式的性质1:不等式的两边都加上(或减)同一个数(或式子),不等号的方向 。
不变
>
如果a>b,c>0,那么ac bc (或 )
c
b
c
a
>
>
如果a>b,c<0,那么ac bc (或 )
c
b
c
a
<
<
类比归纳
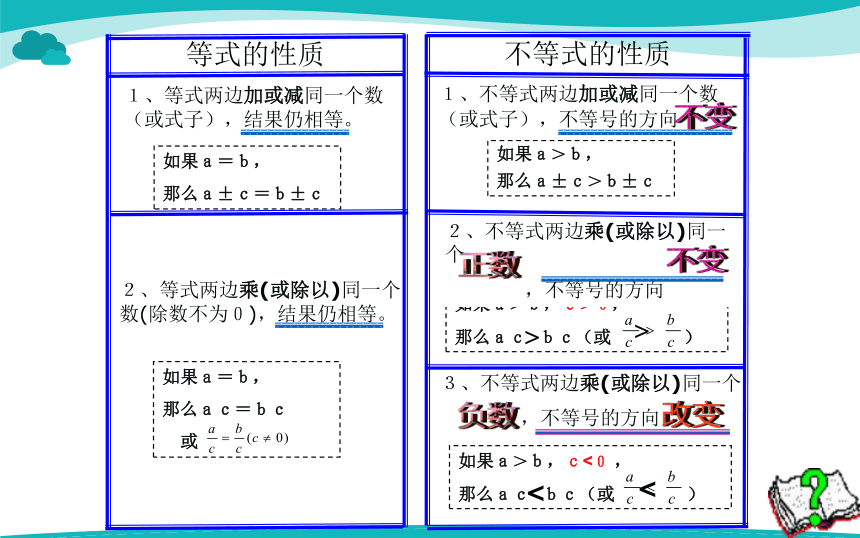
等式性质和不等式性质的相同点和不同点是什么?
如果a>b,c>0,
那么ac bc(或 )
>
>
2、不等式两边乘(或除以)同一个
,不等号的方向
不等式的性质
如果a>b,c<0 ,
那么ac bc(或 )
<
<
3、不等式两边乘(或除以)同一个
,不等号的方向
1、不等式两边加或减同一个数(或式子),不等号的方向
不变
不变
正数
负数
改变
如果a>b,
那么a±c>b±c
1、等式两边加或减同一个数(或式子),结果仍相等。
如果a=b,
那么a±c=b±c
等式的性质
如果a=b,
那么ac=bc
或
2、等式两边乘(或除以)同一个数(除数不为0),结果仍相等。
如果a⑴ a-8 b-8 ⑵ 3a 3b
⑶ -2a -2b (4)
>
1、用“>”或“<”填空:
<
<
>
2、判断下列各题的推导是否正确?为什么?
(1)因为4a>4b,所以a>b;
(2)因为a>3,所以-a>-3;
(3)因为3>2 ,所以 3 + a>2+a;
(4)因为3>2,所以3a>2a.
×
×
要求:
本题由C或D星回答
√
√
分层提高(A层)
(1)∵a-3<b-3,∴ a b( )
(2)∵-4a > -4b,∴a b ( )
(3)若x+1>0,不等式两边同时减1,得 ,依据: 。
(4)若2 x >-6,不等式两边同时除以2,得________,依据 。
(5)若-0.5 x≤1,不等式两边同时乘以-2,得________,依据 。
3、填空:
<
<
x >-1
不等式的性质1
x >-3
不等式的性质2
x≥-2
不等式的性质3
不等式的性质1
不等式的性质3
互助探究2
例1 利用不等式的性质解下列不等式,
并在数轴上表示解集。
(1) x-7 > 26 (2) 3x< 2x+1
(3) (4) -4x>3
> 50
分层提高(B层)
利用不等式的性质解不等式,并把解集在数轴上表示出来:
要求:先独立思考,
再小组交流。
最后由本组B或C星回答
是任意有理数,试比较 与 的大小。
∴
解:∵ 5 >3 ∴
这种解法对吗?如果正确,说出它根据的是不等式的哪一条基本性质;如果不正确,请就明理由。
分层提高(C层)
要求:先独立思考,再小组交流。最后由本组A星回答
课堂练习
1.按下列要求,写出正确的不等式:
(1)由-2<-1,两边都加-a;
(2)由7>5,两边都乘以不为零的-a.
-2-a<-1-a
若a>0,则-a<0,故-7a<-5a;
若a<0,则-a>0,故-7a>-5a;
2.判断正误:
(1)如果a>b,那么ac>bc。
(2)如果a>b,那么ac2>bc2。
(3)如果ac2>bc2, 那么a>b。
×
×
总结归纳
1、这节课你学会了哪些知识和方法?
2、你对本节课的内容还存在哪些疑惑?
3、你对你的学习小组(A.B.C.D星)有何评价建议?
教材98页 第 3题、第5题
作业
质疑是一切新知的来源。
谢谢
9.1.2 不等式的性质
交流预习
四星小组交流预习作业中存在的问题
(2分钟)
要求:B.C.D星把预习作业中的每一个问题先与A星交流,
A星及时指点。
举例说明你是怎样推导出不等式性质的?
互助探究一
正数
不变
负数
改变
不等式的性质2:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
不等式的性质3:不等式的两边都乘以(或除以)同一个_______,不等号的方向______。
如果a>b,那么a±c b±c。
不等式的性质1:不等式的两边都加上(或减)同一个数(或式子),不等号的方向 。
不变
>
如果a>b,c>0,那么ac bc (或 )
c
b
c
a
>
>
如果a>b,c<0,那么ac bc (或 )
c
b
c
a
<
<
类比归纳
等式性质和不等式性质的相同点和不同点是什么?
如果a>b,c>0,
那么ac bc(或 )
>
>
2、不等式两边乘(或除以)同一个
,不等号的方向
不等式的性质
如果a>b,c<0 ,
那么ac bc(或 )
<
<
3、不等式两边乘(或除以)同一个
,不等号的方向
1、不等式两边加或减同一个数(或式子),不等号的方向
不变
不变
正数
负数
改变
如果a>b,
那么a±c>b±c
1、等式两边加或减同一个数(或式子),结果仍相等。
如果a=b,
那么a±c=b±c
等式的性质
如果a=b,
那么ac=bc
或
2、等式两边乘(或除以)同一个数(除数不为0),结果仍相等。
如果a
⑶ -2a -2b (4)
>
1、用“>”或“<”填空:
<
<
>
2、判断下列各题的推导是否正确?为什么?
(1)因为4a>4b,所以a>b;
(2)因为a>3,所以-a>-3;
(3)因为3>2 ,所以 3 + a>2+a;
(4)因为3>2,所以3a>2a.
×
×
要求:
本题由C或D星回答
√
√
分层提高(A层)
(1)∵a-3<b-3,∴ a b( )
(2)∵-4a > -4b,∴a b ( )
(3)若x+1>0,不等式两边同时减1,得 ,依据: 。
(4)若2 x >-6,不等式两边同时除以2,得________,依据 。
(5)若-0.5 x≤1,不等式两边同时乘以-2,得________,依据 。
3、填空:
<
<
x >-1
不等式的性质1
x >-3
不等式的性质2
x≥-2
不等式的性质3
不等式的性质1
不等式的性质3
互助探究2
例1 利用不等式的性质解下列不等式,
并在数轴上表示解集。
(1) x-7 > 26 (2) 3x< 2x+1
(3) (4) -4x>3
> 50
分层提高(B层)
利用不等式的性质解不等式,并把解集在数轴上表示出来:
要求:先独立思考,
再小组交流。
最后由本组B或C星回答
是任意有理数,试比较 与 的大小。
∴
解:∵ 5 >3 ∴
这种解法对吗?如果正确,说出它根据的是不等式的哪一条基本性质;如果不正确,请就明理由。
分层提高(C层)
要求:先独立思考,再小组交流。最后由本组A星回答
课堂练习
1.按下列要求,写出正确的不等式:
(1)由-2<-1,两边都加-a;
(2)由7>5,两边都乘以不为零的-a.
-2-a<-1-a
若a>0,则-a<0,故-7a<-5a;
若a<0,则-a>0,故-7a>-5a;
2.判断正误:
(1)如果a>b,那么ac>bc。
(2)如果a>b,那么ac2>bc2。
(3)如果ac2>bc2, 那么a>b。
×
×
总结归纳
1、这节课你学会了哪些知识和方法?
2、你对本节课的内容还存在哪些疑惑?
3、你对你的学习小组(A.B.C.D星)有何评价建议?
教材98页 第 3题、第5题
作业
质疑是一切新知的来源。
谢谢
