安徽省部分学校2021-2022学年高三上学期期末联考文科数学试题(Word版,含答案)
文档属性
| 名称 | 安徽省部分学校2021-2022学年高三上学期期末联考文科数学试题(Word版,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 00:00:00 | ||
图片预览




文档简介
安徽省部分学校2021-2022学年高三上学期期末联考
文科数学
一 选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1 已知全集,则集合( )
A. B. C. D.
2. 已知复数,则( )
A. B. C. D.
3. 已知整数、满足不等式组,满足条件的整数对个数为( )
A. B. C. D.
4. 某科研机构为了研究一种电子元件某项指标x,y的相关关系,观测得到统计数据如下表:
x 2 4 5 6 8
y 30 40 57 m 69
由此数据得到回归直线方程为,则样本点的残差(观测值减去预报值)为( )
A. 3 B. 2.5 C. D.
5. 函数零点所在的区间为( )
A. B. C. D.
6. 已知一个圆锥形饮料杯的侧面展开图为半圆,销售商在杯内装入部分饮料后,放入一个实心冰球使其恰好淹没在饮料中,则该冰球与饮料的体积比为( )
A. B. C. D.
7. 已知,则曲线在处的切线经过点( )
A B. C. D.
8. 已知数列是首项与公差均为1的等差数列,则( )
A. B. C. D.
9. 双曲函数是一类与三角函数类似的函数,在物理学众多领域中有丰富的实际应用.最基本的双曲函数是双曲正弦函数和双曲余弦函数.令,得到下面结论①为偶函数;②为奇函数;③在上单调递增;④在上单调递减.则以上结论正确的是( )
A. ①③ B. ②③ C. ①④ D. ②④
10. 已知函数,各项互不相等的等比数列满足,记,则( )
A. B. C. D.
11. 已知双曲线的一个焦点关于其中一条渐近线的对称点为,若点P恰在C上,则C的方程为( )
A. B. C. D.
12. 已知为正方体,P,Q,R分别为棱的中点,则①;②平面;③;④,上述四个结论正确的个数为( )
A. 1 B. 2 C. 3 D. 4
二 填空题:本题共4小题,每小题5分,共20分.
13. 已知平面向量,,若,则___________.
14. 已知,若a,b都是从区间中任取的一个数,则满足的概率为___________.
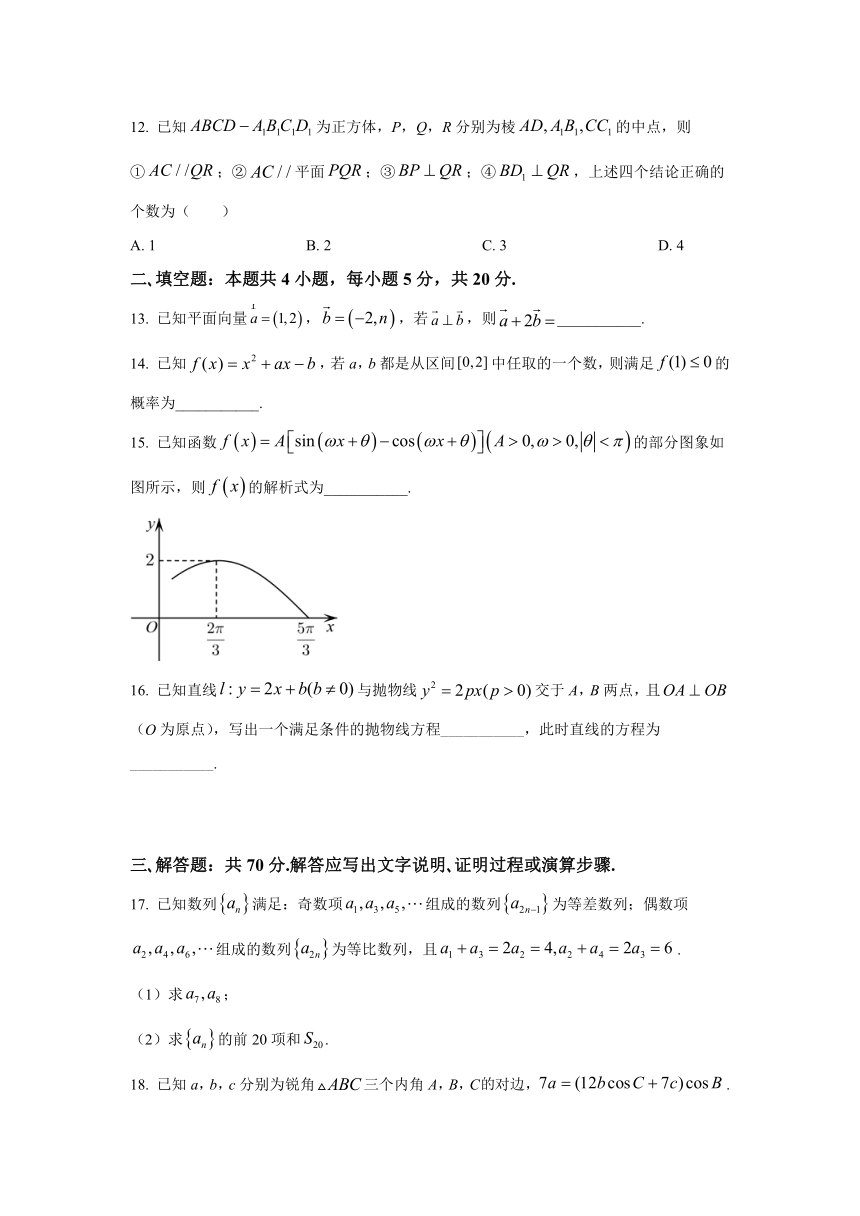
15. 已知函数的部分图象如图所示,则的解析式为___________.
16. 已知直线与抛物线交于A,B两点,且(O为原点),写出一个满足条件的抛物线方程___________,此时直线的方程为___________.
三 解答题:共70分.解答应写出文字说明 证明过程或演算步骤.
17. 已知数列满足:奇数项组成的数列为等差数列;偶数项组成的数列为等比数列,且.
(1)求;
(2)求的前20项和.
18. 已知a,b,c分别为锐角三个内角A,B,C对边,.
(1)求;
(2)若,求的周长.
19. 某小区物业为了让业主有一个良好的居住环境,特制定业主满意度电子调查表,调查表有生活服务 小区环境等多项内容,将每项内容进行分值量化,调查表分值满分为100分.物业管理人员从中随机抽取了100份调查表将其分值作为样本进行统计,作出频率分布直方图如下.
(1)根据频率分布直方图填写各分值段的业主人数表(不必说明理由):
分值
人数
(2)在选取的100位业主中,男士与女士人数相同,规定分值在70分以上为满意,低于70分为不满意,据统计有32位男士满意.请列出列联表,并判断是否有95%的把握认为“业主满意度与性别有关”?
(3)在(2)条件下,物业对满意度分值低于70分的业主进行回访,用分层抽样的方式选出8位业主进行座谈,并从中随机抽取2人为监督员,求恰好抽到男女各一人为监督员的概率.
附:,其中.
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6635 7.879 10.828
20. 如图,四棱锥的底面是矩形,平面平面,E,F分别是的中点.
(1)求证:平面:
(2)求点P到平面的距离.
21. 已知函数.
(1)讨论函数的单调性;
(2)若,求a的取值范围.
22. 已知动点M到直线的距离是M与点距离的倍,记M的轨迹为曲线C.
(1)求曲线C的方程;
(2)动直线与C交于两点A,B,曲线C上是否存在定点P,使得直线的斜率和为零?若存在求出点P坐标;若不存在,请说明理由.
安徽省部分学校2021-2022学年高三上学期期末联考
文科数学 答案版
一 选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1 已知全集,则集合( )
A. B. C. D.
答案 D
2. 已知复数,则( )
A. B. C. D.
答案 D
3. 已知整数、满足不等式组,满足条件的整数对个数为( )
A. B. C. D.
答案 B
4. 某科研机构为了研究一种电子元件某项指标x,y的相关关系,观测得到统计数据如下表:
x 2 4 5 6 8
y 30 40 57 m 69
由此数据得到回归直线方程为,则样本点的残差(观测值减去预报值)为( )
A. 3 B. 2.5 C. D.
答案 D
5. 函数零点所在的区间为( )
A. B. C. D.
答案 C
6. 已知一个圆锥形饮料杯的侧面展开图为半圆,销售商在杯内装入部分饮料后,放入一个实心冰球使其恰好淹没在饮料中,则该冰球与饮料的体积比为( )
A. B. C. D.
答案 C
7. 已知,则曲线在处的切线经过点( )
A B. C. D.
答案 D
8. 已知数列是首项与公差均为1的等差数列,则( )
A. B. C. D.
答案 B
9. 双曲函数是一类与三角函数类似的函数,在物理学众多领域中有丰富的实际应用.最基本的双曲函数是双曲正弦函数和双曲余弦函数.令,得到下面结论①为偶函数;②为奇函数;③在上单调递增;④在上单调递减.则以上结论正确的是( )
A. ①③ B. ②③ C. ①④ D. ②④
答案 B
10. 已知函数,各项互不相等的等比数列满足,记,则( )
A. B. C. D.
答案 D
11. 已知双曲线的一个焦点关于其中一条渐近线的对称点为,若点P恰在C上,则C的方程为( )
A. B. C. D.
答案 A
12. 已知为正方体,P,Q,R分别为棱的中点,则①;②平面;③;④,上述四个结论正确的个数为( )
A. 1 B. 2 C. 3 D. 4
答案 C
二 填空题:本题共4小题,每小题5分,共20分.
13. 已知平面向量,,若,则___________.
答案
14. 已知,若a,b都是从区间中任取的一个数,则满足的概率为___________.
答案 ##0.125
15. 已知函数的部分图象如图所示,则的解析式为___________.
答案 (答案不唯一)
16. 已知直线与抛物线交于A,B两点,且(O为原点),写出一个满足条件的抛物线方程___________,此时直线的方程为___________.
答案 ①. ②.
三 解答题:共70分.解答应写出文字说明 证明过程或演算步骤.
17. 已知数列满足:奇数项组成的数列为等差数列;偶数项组成的数列为等比数列,且.
(1)求;
(2)求的前20项和.
答案 (1),;
(2).
18. 已知a,b,c分别为锐角三个内角A,B,C对边,.
(1)求;
(2)若,求的周长.
答案 (1)
(2)
19. 某小区物业为了让业主有一个良好的居住环境,特制定业主满意度电子调查表,调查表有生活服务 小区环境等多项内容,将每项内容进行分值量化,调查表分值满分为100分.物业管理人员从中随机抽取了100份调查表将其分值作为样本进行统计,作出频率分布直方图如下.
(1)根据频率分布直方图填写各分值段的业主人数表(不必说明理由):
分值
人数
(2)在选取的100位业主中,男士与女士人数相同,规定分值在70分以上为满意,低于70分为不满意,据统计有32位男士满意.请列出列联表,并判断是否有95%的把握认为“业主满意度与性别有关”?
(3)在(2)条件下,物业对满意度分值低于70分的业主进行回访,用分层抽样的方式选出8位业主进行座谈,并从中随机抽取2人为监督员,求恰好抽到男女各一人为监督员的概率.
附:,其中.
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6635 7.879 10.828
答案 (1)答案见解析;
(2)列联表答案见解析,有95%的把握认为“业主满意度与性别有关”;
(3).
20. 如图,四棱锥的底面是矩形,平面平面,E,F分别是的中点.
(1)求证:平面:
(2)求点P到平面的距离.
答案 (1)证明见解析
(2)
21. 已知函数.
(1)讨论函数的单调性;
(2)若,求a的取值范围.
答案 (1)答案见解析
(2)
22. 已知动点M到直线的距离是M与点距离的倍,记M的轨迹为曲线C.
(1)求曲线C的方程;
(2)动直线与C交于两点A,B,曲线C上是否存在定点P,使得直线的斜率和为零?若存在求出点P坐标;若不存在,请说明理由.
答案 (1);
(2)存在,定点或.
文科数学
一 选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1 已知全集,则集合( )
A. B. C. D.
2. 已知复数,则( )
A. B. C. D.
3. 已知整数、满足不等式组,满足条件的整数对个数为( )
A. B. C. D.
4. 某科研机构为了研究一种电子元件某项指标x,y的相关关系,观测得到统计数据如下表:
x 2 4 5 6 8
y 30 40 57 m 69
由此数据得到回归直线方程为,则样本点的残差(观测值减去预报值)为( )
A. 3 B. 2.5 C. D.
5. 函数零点所在的区间为( )
A. B. C. D.
6. 已知一个圆锥形饮料杯的侧面展开图为半圆,销售商在杯内装入部分饮料后,放入一个实心冰球使其恰好淹没在饮料中,则该冰球与饮料的体积比为( )
A. B. C. D.
7. 已知,则曲线在处的切线经过点( )
A B. C. D.
8. 已知数列是首项与公差均为1的等差数列,则( )
A. B. C. D.
9. 双曲函数是一类与三角函数类似的函数,在物理学众多领域中有丰富的实际应用.最基本的双曲函数是双曲正弦函数和双曲余弦函数.令,得到下面结论①为偶函数;②为奇函数;③在上单调递增;④在上单调递减.则以上结论正确的是( )
A. ①③ B. ②③ C. ①④ D. ②④
10. 已知函数,各项互不相等的等比数列满足,记,则( )
A. B. C. D.
11. 已知双曲线的一个焦点关于其中一条渐近线的对称点为,若点P恰在C上,则C的方程为( )
A. B. C. D.
12. 已知为正方体,P,Q,R分别为棱的中点,则①;②平面;③;④,上述四个结论正确的个数为( )
A. 1 B. 2 C. 3 D. 4
二 填空题:本题共4小题,每小题5分,共20分.
13. 已知平面向量,,若,则___________.
14. 已知,若a,b都是从区间中任取的一个数,则满足的概率为___________.
15. 已知函数的部分图象如图所示,则的解析式为___________.
16. 已知直线与抛物线交于A,B两点,且(O为原点),写出一个满足条件的抛物线方程___________,此时直线的方程为___________.
三 解答题:共70分.解答应写出文字说明 证明过程或演算步骤.
17. 已知数列满足:奇数项组成的数列为等差数列;偶数项组成的数列为等比数列,且.
(1)求;
(2)求的前20项和.
18. 已知a,b,c分别为锐角三个内角A,B,C对边,.
(1)求;
(2)若,求的周长.
19. 某小区物业为了让业主有一个良好的居住环境,特制定业主满意度电子调查表,调查表有生活服务 小区环境等多项内容,将每项内容进行分值量化,调查表分值满分为100分.物业管理人员从中随机抽取了100份调查表将其分值作为样本进行统计,作出频率分布直方图如下.
(1)根据频率分布直方图填写各分值段的业主人数表(不必说明理由):
分值
人数
(2)在选取的100位业主中,男士与女士人数相同,规定分值在70分以上为满意,低于70分为不满意,据统计有32位男士满意.请列出列联表,并判断是否有95%的把握认为“业主满意度与性别有关”?
(3)在(2)条件下,物业对满意度分值低于70分的业主进行回访,用分层抽样的方式选出8位业主进行座谈,并从中随机抽取2人为监督员,求恰好抽到男女各一人为监督员的概率.
附:,其中.
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6635 7.879 10.828
20. 如图,四棱锥的底面是矩形,平面平面,E,F分别是的中点.
(1)求证:平面:
(2)求点P到平面的距离.
21. 已知函数.
(1)讨论函数的单调性;
(2)若,求a的取值范围.
22. 已知动点M到直线的距离是M与点距离的倍,记M的轨迹为曲线C.
(1)求曲线C的方程;
(2)动直线与C交于两点A,B,曲线C上是否存在定点P,使得直线的斜率和为零?若存在求出点P坐标;若不存在,请说明理由.
安徽省部分学校2021-2022学年高三上学期期末联考
文科数学 答案版
一 选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1 已知全集,则集合( )
A. B. C. D.
答案 D
2. 已知复数,则( )
A. B. C. D.
答案 D
3. 已知整数、满足不等式组,满足条件的整数对个数为( )
A. B. C. D.
答案 B
4. 某科研机构为了研究一种电子元件某项指标x,y的相关关系,观测得到统计数据如下表:
x 2 4 5 6 8
y 30 40 57 m 69
由此数据得到回归直线方程为,则样本点的残差(观测值减去预报值)为( )
A. 3 B. 2.5 C. D.
答案 D
5. 函数零点所在的区间为( )
A. B. C. D.
答案 C
6. 已知一个圆锥形饮料杯的侧面展开图为半圆,销售商在杯内装入部分饮料后,放入一个实心冰球使其恰好淹没在饮料中,则该冰球与饮料的体积比为( )
A. B. C. D.
答案 C
7. 已知,则曲线在处的切线经过点( )
A B. C. D.
答案 D
8. 已知数列是首项与公差均为1的等差数列,则( )
A. B. C. D.
答案 B
9. 双曲函数是一类与三角函数类似的函数,在物理学众多领域中有丰富的实际应用.最基本的双曲函数是双曲正弦函数和双曲余弦函数.令,得到下面结论①为偶函数;②为奇函数;③在上单调递增;④在上单调递减.则以上结论正确的是( )
A. ①③ B. ②③ C. ①④ D. ②④
答案 B
10. 已知函数,各项互不相等的等比数列满足,记,则( )
A. B. C. D.
答案 D
11. 已知双曲线的一个焦点关于其中一条渐近线的对称点为,若点P恰在C上,则C的方程为( )
A. B. C. D.
答案 A
12. 已知为正方体,P,Q,R分别为棱的中点,则①;②平面;③;④,上述四个结论正确的个数为( )
A. 1 B. 2 C. 3 D. 4
答案 C
二 填空题:本题共4小题,每小题5分,共20分.
13. 已知平面向量,,若,则___________.
答案
14. 已知,若a,b都是从区间中任取的一个数,则满足的概率为___________.
答案 ##0.125
15. 已知函数的部分图象如图所示,则的解析式为___________.
答案 (答案不唯一)
16. 已知直线与抛物线交于A,B两点,且(O为原点),写出一个满足条件的抛物线方程___________,此时直线的方程为___________.
答案 ①. ②.
三 解答题:共70分.解答应写出文字说明 证明过程或演算步骤.
17. 已知数列满足:奇数项组成的数列为等差数列;偶数项组成的数列为等比数列,且.
(1)求;
(2)求的前20项和.
答案 (1),;
(2).
18. 已知a,b,c分别为锐角三个内角A,B,C对边,.
(1)求;
(2)若,求的周长.
答案 (1)
(2)
19. 某小区物业为了让业主有一个良好的居住环境,特制定业主满意度电子调查表,调查表有生活服务 小区环境等多项内容,将每项内容进行分值量化,调查表分值满分为100分.物业管理人员从中随机抽取了100份调查表将其分值作为样本进行统计,作出频率分布直方图如下.
(1)根据频率分布直方图填写各分值段的业主人数表(不必说明理由):
分值
人数
(2)在选取的100位业主中,男士与女士人数相同,规定分值在70分以上为满意,低于70分为不满意,据统计有32位男士满意.请列出列联表,并判断是否有95%的把握认为“业主满意度与性别有关”?
(3)在(2)条件下,物业对满意度分值低于70分的业主进行回访,用分层抽样的方式选出8位业主进行座谈,并从中随机抽取2人为监督员,求恰好抽到男女各一人为监督员的概率.
附:,其中.
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6635 7.879 10.828
答案 (1)答案见解析;
(2)列联表答案见解析,有95%的把握认为“业主满意度与性别有关”;
(3).
20. 如图,四棱锥的底面是矩形,平面平面,E,F分别是的中点.
(1)求证:平面:
(2)求点P到平面的距离.
答案 (1)证明见解析
(2)
21. 已知函数.
(1)讨论函数的单调性;
(2)若,求a的取值范围.
答案 (1)答案见解析
(2)
22. 已知动点M到直线的距离是M与点距离的倍,记M的轨迹为曲线C.
(1)求曲线C的方程;
(2)动直线与C交于两点A,B,曲线C上是否存在定点P,使得直线的斜率和为零?若存在求出点P坐标;若不存在,请说明理由.
答案 (1);
(2)存在,定点或.
同课章节目录
