安徽省阜阳市2021-2022学年高三上学期期末教学质量统测文科数学试题(Word版,含答案)
文档属性
| 名称 | 安徽省阜阳市2021-2022学年高三上学期期末教学质量统测文科数学试题(Word版,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 881.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 00:00:00 | ||
图片预览




文档简介
阜阳市2021-2022学年高三上学期期末教学质量统测
数学(文科)
一 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则( )
A B. C. D.
2. 为虚数单位,若,则( )
A. B. C. D.
3. 下列函数为奇函数的是( )
A. B. C. D.
4. 函数的图象大致为( )
A. B.
C. D.
5. 数学界有很多著名的猜想,角谷猜想就是其中之一.它是指一个正整数,如果是奇数就乘以3再加1,如果是偶数就除以2,经过这样若干次运算,最终回到1.现给定正整数10,按上述运算规则,回到1时经过的运算次数至少为( )
A 5 B. 6 C. 7 D. 8
6. 已知双曲线的顶点到渐近线的距离为,则C的离心率为( )
A. B. C. 2 D. 5
7. 在正四面体中,点是的中点,则与所成角的正弦值为( )
A. B. C. D.
8. 某高中生周末自主学习时,进行了一次数学探究活动,他将一天的日期与星期用有序数对表示,比如某个月10日,11日是周末,就分别用和表示,然后在平面直角坐标系内描出对应的点.他查阅了某年七月份的日历,利用数学软件在平面直角坐标系内描出了31个点,经过思考,他构造了函数,使得这些点都在的图象上,若,则下列叙述正确的是( )
A. 该月12日是星期二,有五天是星期二 B. 该月12日是星期一,有四天是星期二
C. 该月23日是星期六,有五天是星期六 D. 该月23日是星期二,有四天是星期二
9. 若函数有唯一的极值点,则实数a的取值范围为( )
A. B. C. D.
10. 已知,则a,b,c的大小关系为( )
A. B. C. D.
11. 点M在边长为2的正三角形内(包括边界),满足,则的取值范围是( )
A. B. C. D.
12. 在长方体中,,E,F分别为和的中点,则( )
A.
B. 三棱锥的体积为
C. 三棱锥外接球的表面积为
D. 三棱锥外接球球心到平面距离为
二 填空题:本大题共4小题,每小题5分,共20分.把答案填写在答题卡相应的位置.
13. 已知x,y满足约束条件,则的最大值为___________.
14. 某同学去北京参加清华大学冬令营活动,从阜阳出发,统一到合肥集中,再从合肥去往北京,在他可行的时间内,从阜阳到合肥有班高铁,班汽车,从合肥到北京有班飞机,班高铁,则该同学都是乘高铁去北京的概率为___________.
15. 若函数的最大值为2,则的一个可能的取值为___________.
16. 设抛物线的准线为l,焦点为F,以点为圆心的圆过点F且与l相切,点A,B分别在C与l上,点O为原点,,则___________.
三 解答题:本大题共6小题,共70分.解答应写出必要的文字说明 证明过程或演算步骤.
17. 内角A,B,C的对边分别为a,b,c,已知,且的面积为.
(1)求角A;
(2)若,求的周长.
18. 记数列的前n项和为,满足,且.
(1)证明:数列是等差数列;
(2)设数列满足,求的前n项和.
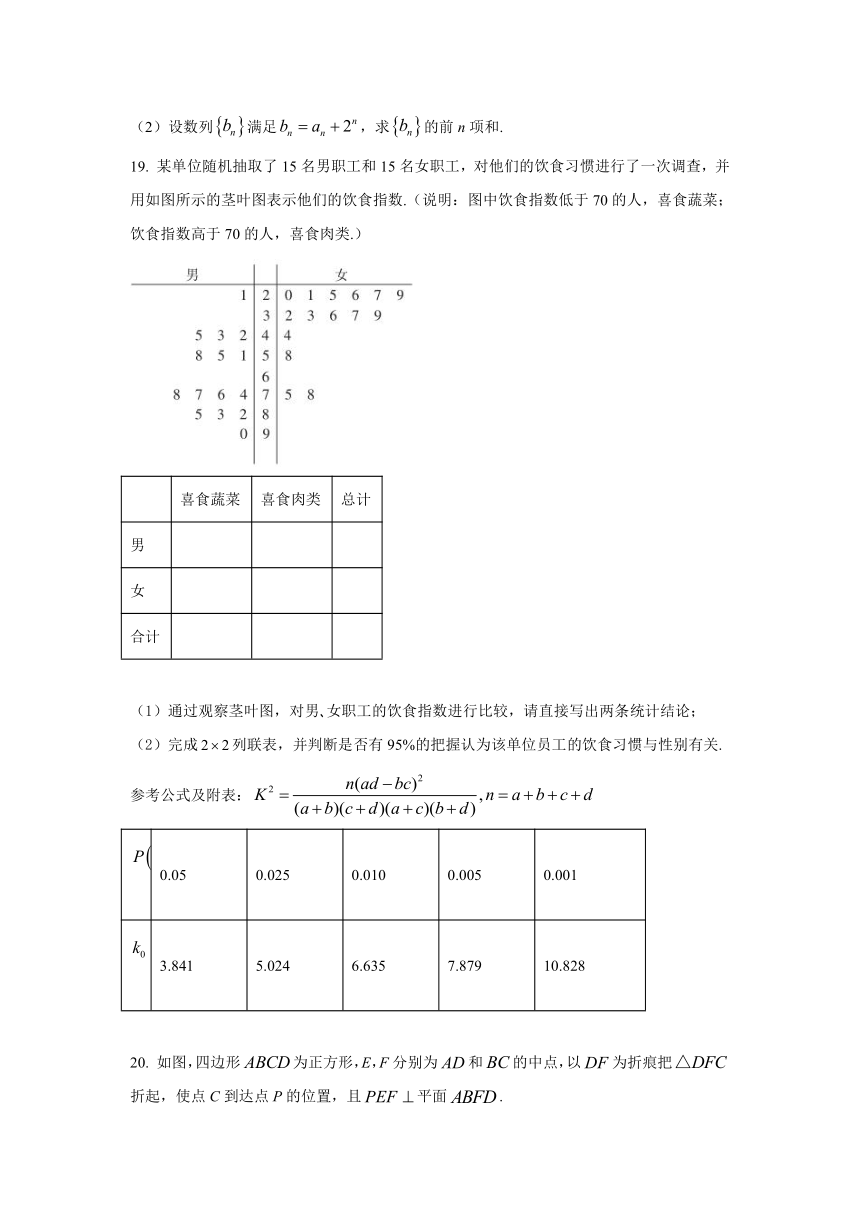
19. 某单位随机抽取了15名男职工和15名女职工,对他们的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数.(说明:图中饮食指数低于70的人,喜食蔬菜;饮食指数高于70的人,喜食肉类.)
喜食蔬菜 喜食肉类 总计
男
女
合计
(1)通过观察茎叶图,对男 女职工的饮食指数进行比较,请直接写出两条统计结论;
(2)完成列联表,并判断是否有95%的把握认为该单位员工的饮食习惯与性别有关.
参考公式及附表:
0.05 0.025 0.010 0.005 0.001
3.841 5.024 6.635 7.879 10.828
20. 如图,四边形为正方形,E,F分别为和的中点,以为折痕把折起,使点C到达点P的位置,且平面.
(1)证明:;
(2)若,求三棱锥的体积.
21. 已知椭圆的离心率为,C的左,右焦点分别为,A,B是C上关于原点对称的两点,四边形的周长为.
(1)求C的方程;
(2)设分别为直线和的斜率,求的取值范围.
22. 已知函数.
(1)若有两个零点,求实数a的取值范围;
(2)设曲线过原点的切线为,在点处的切线为,证明:与y轴围成的区域G的面积S为定值.
阜阳市2021-2022学年高三上学期期末教学质量统测
数学(文科) 答案版
一 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则( )
A B. C. D.
答案 B
2. 为虚数单位,若,则( )
A. B. C. D.
答案 B
3. 下列函数为奇函数的是( )
A. B. C. D.
答案 D
4. 函数的图象大致为( )
A. B.
C. D.
答案 A
5. 数学界有很多著名的猜想,角谷猜想就是其中之一.它是指一个正整数,如果是奇数就乘以3再加1,如果是偶数就除以2,经过这样若干次运算,最终回到1.现给定正整数10,按上述运算规则,回到1时经过的运算次数至少为( )
A 5 B. 6 C. 7 D. 8
答案 B
6. 已知双曲线的顶点到渐近线的距离为,则C的离心率为( )
A. B. C. 2 D. 5
答案 C
7. 在正四面体中,点是的中点,则与所成角的正弦值为( )
A. B. C. D.
答案 A
8. 某高中生周末自主学习时,进行了一次数学探究活动,他将一天的日期与星期用有序数对表示,比如某个月10日,11日是周末,就分别用和表示,然后在平面直角坐标系内描出对应的点.他查阅了某年七月份的日历,利用数学软件在平面直角坐标系内描出了31个点,经过思考,他构造了函数,使得这些点都在的图象上,若,则下列叙述正确的是( )
A. 该月12日是星期二,有五天是星期二 B. 该月12日是星期一,有四天是星期二
C. 该月23日是星期六,有五天是星期六 D. 该月23日是星期二,有四天是星期二
答案 C
9. 若函数有唯一的极值点,则实数a的取值范围为( )
A. B. C. D.
答案 C
10. 已知,则a,b,c的大小关系为( )
A. B. C. D.
答案 D
11. 点M在边长为2的正三角形内(包括边界),满足,则的取值范围是( )
A. B. C. D.
答案 B
12. 在长方体中,,E,F分别为和的中点,则( )
A.
B. 三棱锥的体积为
C. 三棱锥外接球的表面积为
D. 三棱锥外接球球心到平面距离为
答案 D
二 填空题:本大题共4小题,每小题5分,共20分.把答案填写在答题卡相应的位置.
13. 已知x,y满足约束条件,则的最大值为___________.
答案 4
14. 某同学去北京参加清华大学冬令营活动,从阜阳出发,统一到合肥集中,再从合肥去往北京,在他可行的时间内,从阜阳到合肥有班高铁,班汽车,从合肥到北京有班飞机,班高铁,则该同学都是乘高铁去北京的概率为___________.
答案 ##
15. 若函数的最大值为2,则的一个可能的取值为___________.
答案 (答案不唯一)
16. 设抛物线的准线为l,焦点为F,以点为圆心的圆过点F且与l相切,点A,B分别在C与l上,点O为原点,,则___________.
答案 ##
三 解答题:本大题共6小题,共70分.解答应写出必要的文字说明 证明过程或演算步骤.
17. 内角A,B,C的对边分别为a,b,c,已知,且的面积为.
(1)求角A;
(2)若,求的周长.
答案 (1)
(2)
18. 记数列的前n项和为,满足,且.
(1)证明:数列是等差数列;
(2)设数列满足,求的前n项和.
答案 (1)证明见解析
(2)前n项和为
19. 某单位随机抽取了15名男职工和15名女职工,对他们的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数.(说明:图中饮食指数低于70的人,喜食蔬菜;饮食指数高于70的人,喜食肉类.)
喜食蔬菜 喜食肉类 总计
男
女
合计
(1)通过观察茎叶图,对男 女职工的饮食指数进行比较,请直接写出两条统计结论;
(2)完成列联表,并判断是否有95%的把握认为该单位员工的饮食习惯与性别有关.
参考公式及附表:
0.05 0.025 0.010 0.005 0.001
3.841 5.024 6.635 7.879 10.828
答案 (1)答案见解析
(2)列联表答案见解析,有95%的把握认为该单位员工的饮食习惯与性别有关
20. 如图,四边形为正方形,E,F分别为和的中点,以为折痕把折起,使点C到达点P的位置,且平面.
(1)证明:;
(2)若,求三棱锥的体积.
答案 (1)证明见解析
(2)
21. 已知椭圆的离心率为,C的左,右焦点分别为,A,B是C上关于原点对称的两点,四边形的周长为.
(1)求C的方程;
(2)设分别为直线和的斜率,求的取值范围.
答案 (1)
(2)
22. 已知函数.
(1)若有两个零点,求实数a的取值范围;
(2)设曲线过原点的切线为,在点处的切线为,证明:与y轴围成的区域G的面积S为定值.
答案 (1)
(2)证明见解析
数学(文科)
一 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则( )
A B. C. D.
2. 为虚数单位,若,则( )
A. B. C. D.
3. 下列函数为奇函数的是( )
A. B. C. D.
4. 函数的图象大致为( )
A. B.
C. D.
5. 数学界有很多著名的猜想,角谷猜想就是其中之一.它是指一个正整数,如果是奇数就乘以3再加1,如果是偶数就除以2,经过这样若干次运算,最终回到1.现给定正整数10,按上述运算规则,回到1时经过的运算次数至少为( )
A 5 B. 6 C. 7 D. 8
6. 已知双曲线的顶点到渐近线的距离为,则C的离心率为( )
A. B. C. 2 D. 5
7. 在正四面体中,点是的中点,则与所成角的正弦值为( )
A. B. C. D.
8. 某高中生周末自主学习时,进行了一次数学探究活动,他将一天的日期与星期用有序数对表示,比如某个月10日,11日是周末,就分别用和表示,然后在平面直角坐标系内描出对应的点.他查阅了某年七月份的日历,利用数学软件在平面直角坐标系内描出了31个点,经过思考,他构造了函数,使得这些点都在的图象上,若,则下列叙述正确的是( )
A. 该月12日是星期二,有五天是星期二 B. 该月12日是星期一,有四天是星期二
C. 该月23日是星期六,有五天是星期六 D. 该月23日是星期二,有四天是星期二
9. 若函数有唯一的极值点,则实数a的取值范围为( )
A. B. C. D.
10. 已知,则a,b,c的大小关系为( )
A. B. C. D.
11. 点M在边长为2的正三角形内(包括边界),满足,则的取值范围是( )
A. B. C. D.
12. 在长方体中,,E,F分别为和的中点,则( )
A.
B. 三棱锥的体积为
C. 三棱锥外接球的表面积为
D. 三棱锥外接球球心到平面距离为
二 填空题:本大题共4小题,每小题5分,共20分.把答案填写在答题卡相应的位置.
13. 已知x,y满足约束条件,则的最大值为___________.
14. 某同学去北京参加清华大学冬令营活动,从阜阳出发,统一到合肥集中,再从合肥去往北京,在他可行的时间内,从阜阳到合肥有班高铁,班汽车,从合肥到北京有班飞机,班高铁,则该同学都是乘高铁去北京的概率为___________.
15. 若函数的最大值为2,则的一个可能的取值为___________.
16. 设抛物线的准线为l,焦点为F,以点为圆心的圆过点F且与l相切,点A,B分别在C与l上,点O为原点,,则___________.
三 解答题:本大题共6小题,共70分.解答应写出必要的文字说明 证明过程或演算步骤.
17. 内角A,B,C的对边分别为a,b,c,已知,且的面积为.
(1)求角A;
(2)若,求的周长.
18. 记数列的前n项和为,满足,且.
(1)证明:数列是等差数列;
(2)设数列满足,求的前n项和.
19. 某单位随机抽取了15名男职工和15名女职工,对他们的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数.(说明:图中饮食指数低于70的人,喜食蔬菜;饮食指数高于70的人,喜食肉类.)
喜食蔬菜 喜食肉类 总计
男
女
合计
(1)通过观察茎叶图,对男 女职工的饮食指数进行比较,请直接写出两条统计结论;
(2)完成列联表,并判断是否有95%的把握认为该单位员工的饮食习惯与性别有关.
参考公式及附表:
0.05 0.025 0.010 0.005 0.001
3.841 5.024 6.635 7.879 10.828
20. 如图,四边形为正方形,E,F分别为和的中点,以为折痕把折起,使点C到达点P的位置,且平面.
(1)证明:;
(2)若,求三棱锥的体积.
21. 已知椭圆的离心率为,C的左,右焦点分别为,A,B是C上关于原点对称的两点,四边形的周长为.
(1)求C的方程;
(2)设分别为直线和的斜率,求的取值范围.
22. 已知函数.
(1)若有两个零点,求实数a的取值范围;
(2)设曲线过原点的切线为,在点处的切线为,证明:与y轴围成的区域G的面积S为定值.
阜阳市2021-2022学年高三上学期期末教学质量统测
数学(文科) 答案版
一 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则( )
A B. C. D.
答案 B
2. 为虚数单位,若,则( )
A. B. C. D.
答案 B
3. 下列函数为奇函数的是( )
A. B. C. D.
答案 D
4. 函数的图象大致为( )
A. B.
C. D.
答案 A
5. 数学界有很多著名的猜想,角谷猜想就是其中之一.它是指一个正整数,如果是奇数就乘以3再加1,如果是偶数就除以2,经过这样若干次运算,最终回到1.现给定正整数10,按上述运算规则,回到1时经过的运算次数至少为( )
A 5 B. 6 C. 7 D. 8
答案 B
6. 已知双曲线的顶点到渐近线的距离为,则C的离心率为( )
A. B. C. 2 D. 5
答案 C
7. 在正四面体中,点是的中点,则与所成角的正弦值为( )
A. B. C. D.
答案 A
8. 某高中生周末自主学习时,进行了一次数学探究活动,他将一天的日期与星期用有序数对表示,比如某个月10日,11日是周末,就分别用和表示,然后在平面直角坐标系内描出对应的点.他查阅了某年七月份的日历,利用数学软件在平面直角坐标系内描出了31个点,经过思考,他构造了函数,使得这些点都在的图象上,若,则下列叙述正确的是( )
A. 该月12日是星期二,有五天是星期二 B. 该月12日是星期一,有四天是星期二
C. 该月23日是星期六,有五天是星期六 D. 该月23日是星期二,有四天是星期二
答案 C
9. 若函数有唯一的极值点,则实数a的取值范围为( )
A. B. C. D.
答案 C
10. 已知,则a,b,c的大小关系为( )
A. B. C. D.
答案 D
11. 点M在边长为2的正三角形内(包括边界),满足,则的取值范围是( )
A. B. C. D.
答案 B
12. 在长方体中,,E,F分别为和的中点,则( )
A.
B. 三棱锥的体积为
C. 三棱锥外接球的表面积为
D. 三棱锥外接球球心到平面距离为
答案 D
二 填空题:本大题共4小题,每小题5分,共20分.把答案填写在答题卡相应的位置.
13. 已知x,y满足约束条件,则的最大值为___________.
答案 4
14. 某同学去北京参加清华大学冬令营活动,从阜阳出发,统一到合肥集中,再从合肥去往北京,在他可行的时间内,从阜阳到合肥有班高铁,班汽车,从合肥到北京有班飞机,班高铁,则该同学都是乘高铁去北京的概率为___________.
答案 ##
15. 若函数的最大值为2,则的一个可能的取值为___________.
答案 (答案不唯一)
16. 设抛物线的准线为l,焦点为F,以点为圆心的圆过点F且与l相切,点A,B分别在C与l上,点O为原点,,则___________.
答案 ##
三 解答题:本大题共6小题,共70分.解答应写出必要的文字说明 证明过程或演算步骤.
17. 内角A,B,C的对边分别为a,b,c,已知,且的面积为.
(1)求角A;
(2)若,求的周长.
答案 (1)
(2)
18. 记数列的前n项和为,满足,且.
(1)证明:数列是等差数列;
(2)设数列满足,求的前n项和.
答案 (1)证明见解析
(2)前n项和为
19. 某单位随机抽取了15名男职工和15名女职工,对他们的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数.(说明:图中饮食指数低于70的人,喜食蔬菜;饮食指数高于70的人,喜食肉类.)
喜食蔬菜 喜食肉类 总计
男
女
合计
(1)通过观察茎叶图,对男 女职工的饮食指数进行比较,请直接写出两条统计结论;
(2)完成列联表,并判断是否有95%的把握认为该单位员工的饮食习惯与性别有关.
参考公式及附表:
0.05 0.025 0.010 0.005 0.001
3.841 5.024 6.635 7.879 10.828
答案 (1)答案见解析
(2)列联表答案见解析,有95%的把握认为该单位员工的饮食习惯与性别有关
20. 如图,四边形为正方形,E,F分别为和的中点,以为折痕把折起,使点C到达点P的位置,且平面.
(1)证明:;
(2)若,求三棱锥的体积.
答案 (1)证明见解析
(2)
21. 已知椭圆的离心率为,C的左,右焦点分别为,A,B是C上关于原点对称的两点,四边形的周长为.
(1)求C的方程;
(2)设分别为直线和的斜率,求的取值范围.
答案 (1)
(2)
22. 已知函数.
(1)若有两个零点,求实数a的取值范围;
(2)设曲线过原点的切线为,在点处的切线为,证明:与y轴围成的区域G的面积S为定值.
答案 (1)
(2)证明见解析
同课章节目录
