安徽省芜湖市2021-2022学年高三上学期期末考试文科数学试题(Word版,含答案)
文档属性
| 名称 | 安徽省芜湖市2021-2022学年高三上学期期末考试文科数学试题(Word版,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 00:00:00 | ||
图片预览




文档简介
芜湖市2021-2022学年高三上学期期末考试
数学(文科)试题卷
一 选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 集合中的元素个数是( )
A. 0 B. 4 C. 5 D. 6
2. 复数的虚部是( )
A. B. C. D.
3. 徽砚又名歙砚,中国四大名砚之一,是砚史上与端砚齐名珍品.以砚石在古歙州府加工和集散而得名,徽砚始于唐代,据北宋唐积《歙州砚谱》载:婺源砚在唐开元中,猎人叶氏逐兽至长城里,见叠石如城垒状,莹洁可爱,因携之归,刊出成砚,温润大过端溪,此后,徽砚名闻天下,如图所示的徽砚近似底面直径为,高为的圆柱体,则该徽砚的体积为( )
A. B. C. D.
4. 已知,,则p是q( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5. 已知等差数列,公差为,且、、成等比数列,则( )
A. B. C. D.
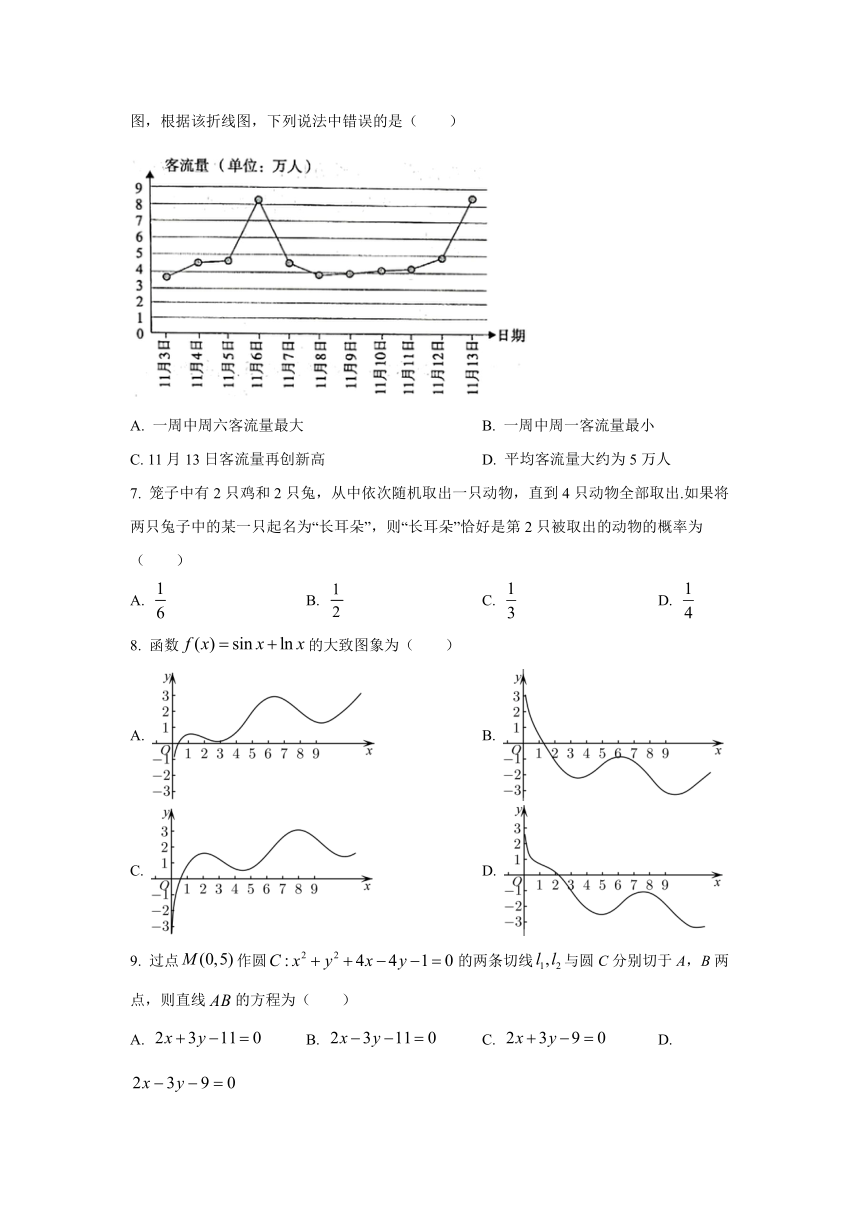
6. 芜湖市轻轨成为城市发展的新亮点,一号线自2021年11月3日(周三)正式运行以来,给本地居民出行带来极大的便捷.如图为轻轨一号线正式运行后连续若干天的客流量折线图,根据该折线图,下列说法中错误的是( )
A. 一周中周六客流量最大 B. 一周中周一客流量最小
C. 11月13日客流量再创新高 D. 平均客流量大约为5万人
7. 笼子中有2只鸡和2只兔,从中依次随机取出一只动物,直到4只动物全部取出.如果将两只兔子中的某一只起名为“长耳朵”,则“长耳朵”恰好是第2只被取出的动物的概率为( )
A. B. C. D.
8. 函数的大致图象为( )
A. B.
C. D.
9. 过点作圆的两条切线与圆C分别切于A,B两点,则直线的方程为( )
A. B. C. D.
10. 已知点P为双曲线的左支上一点,O为坐标原点,为双曲线的左,右焦点.且,则双曲线的离心率为( )
A. B. C. D.
11. 已知函数,则下列说法正确的是( )
A 关于直线对称 B. 关于点对称
C 关于点对称 D. 关于直线对称
12. 如图所示,在长方体中,,,则该长方体外接球球心到平面的距离为( )
A B. C. D.
二 填空题:本题共4小题,每小题5分,共20分.
13. 若x,y满足约束条件则的最大值为___________.
14. 已知向量是互相垂直的两个单位向量,若,则___________.
15. 将函数的图象上所有点的横坐标变为原来的倍,纵坐标不变,再将所得图象向右平移个单位,得到函数的图象,当时,值域为___________.
16. 若函数有两个极值点,则实数a的取值范围是___________.
三 解答题:共70分.解答应写出文字说明 证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22 23题为选考题,考生根据要求作答.
17. 在中,角A,B,C的对边分别为a,b,c,.
(1)求;
(2)若,求的面积.
18. 某校新入学的500名高一学生订购校服的尺码柱状图如下图所示:
(1)请根据同学订购校服的尺码柱状图估算该校高一同学的平均身高;
(2)从入学体检可知该校高一男同学平均身高为,女同学平均身高为,请根据体检数据计算出该校高一学生平均身高,并分析(1)中的估算值与由体检数据得出的平均值存在差异的原因.
19. 已知函数在处切线与x轴平行.
(1)求在区间上的最值;
(2)若恰有两个零点,且在上恒成立,求实数c的取值范围.
20. 如图所示,在等腰梯形中,,在等腰梯形中,,将等腰梯形沿所在直线翻折,使得E,F在平面上的射影恰好与A,B重合.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
21. 已知椭圆的焦距为2,分别是C的左右两个焦点,椭圆C上满足的点P有且只有两个.
(1)求椭圆C的标准方程;
(2)若直线l与椭圆C交于A,B两点,且,求证:存在定点Q,使得Q到直线l的距离为定值,并求出这个定值.
22. 平面直角坐标系中,直线l的参数方程为(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设点,直线l交曲线C于A,B两点,求的值.
23. 已知函数.
(1)求满足不等式的实数m的取值范围;
(2)记的最小值为k,若,且,证明:.
芜湖市2021-2022学年高三上学期期末考试
数学(文科)试题卷 答案版
一 选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 集合中的元素个数是( )
A. 0 B. 4 C. 5 D. 6
【答案】B
2. 复数的虚部是( )
A. B. C. D.
【答案】A
3. 徽砚又名歙砚,中国四大名砚之一,是砚史上与端砚齐名珍品.以砚石在古歙州府加工和集散而得名,徽砚始于唐代,据北宋唐积《歙州砚谱》载:婺源砚在唐开元中,猎人叶氏逐兽至长城里,见叠石如城垒状,莹洁可爱,因携之归,刊出成砚,温润大过端溪,此后,徽砚名闻天下,如图所示的徽砚近似底面直径为,高为的圆柱体,则该徽砚的体积为( )
A. B. C. D.
【答案】C
4. 已知,,则p是q( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】B
5. 已知等差数列,公差为,且、、成等比数列,则( )
A. B. C. D.
【答案】D
6. 芜湖市轻轨成为城市发展的新亮点,一号线自2021年11月3日(周三)正式运行以来,给本地居民出行带来极大的便捷.如图为轻轨一号线正式运行后连续若干天的客流量折线图,根据该折线图,下列说法中错误的是( )
A. 一周中周六客流量最大 B. 一周中周一客流量最小
C. 11月13日客流量再创新高 D. 平均客流量大约为5万人
【答案】B
7. 笼子中有2只鸡和2只兔,从中依次随机取出一只动物,直到4只动物全部取出.如果将两只兔子中的某一只起名为“长耳朵”,则“长耳朵”恰好是第2只被取出的动物的概率为( )
A. B. C. D.
【答案】D
8. 函数的大致图象为( )
A. B.
C. D.
【答案】C
9. 过点作圆的两条切线与圆C分别切于A,B两点,则直线的方程为( )
A. B. C. D.
【答案】A
10. 已知点P为双曲线的左支上一点,O为坐标原点,为双曲线的左,右焦点.且,则双曲线的离心率为( )
A. B. C. D.
【答案】B
11. 已知函数,则下列说法正确的是( )
A 关于直线对称 B. 关于点对称
C 关于点对称 D. 关于直线对称
【答案】B
12. 如图所示,在长方体中,,,则该长方体外接球球心到平面的距离为( )
A B. C. D.
【答案】A
二 填空题:本题共4小题,每小题5分,共20分.
13. 若x,y满足约束条件则的最大值为___________.
【答案】5
14. 已知向量是互相垂直的两个单位向量,若,则___________.
【答案】
15. 将函数的图象上所有点的横坐标变为原来的倍,纵坐标不变,再将所得图象向右平移个单位,得到函数的图象,当时,值域为___________.
【答案】
16. 若函数有两个极值点,则实数a的取值范围是___________.
【答案】
三 解答题:共70分.解答应写出文字说明 证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22 23题为选考题,考生根据要求作答.
17. 在中,角A,B,C的对边分别为a,b,c,.
(1)求;
(2)若,求的面积.
【答案】(1);
(2)14.
18. 某校新入学的500名高一学生订购校服的尺码柱状图如下图所示:
(1)请根据同学订购校服的尺码柱状图估算该校高一同学的平均身高;
(2)从入学体检可知该校高一男同学平均身高为,女同学平均身高为,请根据体检数据计算出该校高一学生平均身高,并分析(1)中的估算值与由体检数据得出的平均值存在差异的原因.
【答案】(1)
(2),分析答案见解析
19. 已知函数在处切线与x轴平行.
(1)求在区间上的最值;
(2)若恰有两个零点,且在上恒成立,求实数c的取值范围.
【答案】(1)最小值为,最大值为;
(2).
20. 如图所示,在等腰梯形中,,在等腰梯形中,,将等腰梯形沿所在直线翻折,使得E,F在平面上的射影恰好与A,B重合.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
21. 已知椭圆的焦距为2,分别是C的左右两个焦点,椭圆C上满足的点P有且只有两个.
(1)求椭圆C的标准方程;
(2)若直线l与椭圆C交于A,B两点,且,求证:存在定点Q,使得Q到直线l的距离为定值,并求出这个定值.
【答案】(1);
(2)证明见解析,定值.
22. 平面直角坐标系中,直线l的参数方程为(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设点,直线l交曲线C于A,B两点,求的值.
【答案】(1),
(2)
23. 已知函数.
(1)求满足不等式的实数m的取值范围;
(2)记的最小值为k,若,且,证明:.
【答案】(1);
(2)证明见解析.
数学(文科)试题卷
一 选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 集合中的元素个数是( )
A. 0 B. 4 C. 5 D. 6
2. 复数的虚部是( )
A. B. C. D.
3. 徽砚又名歙砚,中国四大名砚之一,是砚史上与端砚齐名珍品.以砚石在古歙州府加工和集散而得名,徽砚始于唐代,据北宋唐积《歙州砚谱》载:婺源砚在唐开元中,猎人叶氏逐兽至长城里,见叠石如城垒状,莹洁可爱,因携之归,刊出成砚,温润大过端溪,此后,徽砚名闻天下,如图所示的徽砚近似底面直径为,高为的圆柱体,则该徽砚的体积为( )
A. B. C. D.
4. 已知,,则p是q( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5. 已知等差数列,公差为,且、、成等比数列,则( )
A. B. C. D.
6. 芜湖市轻轨成为城市发展的新亮点,一号线自2021年11月3日(周三)正式运行以来,给本地居民出行带来极大的便捷.如图为轻轨一号线正式运行后连续若干天的客流量折线图,根据该折线图,下列说法中错误的是( )
A. 一周中周六客流量最大 B. 一周中周一客流量最小
C. 11月13日客流量再创新高 D. 平均客流量大约为5万人
7. 笼子中有2只鸡和2只兔,从中依次随机取出一只动物,直到4只动物全部取出.如果将两只兔子中的某一只起名为“长耳朵”,则“长耳朵”恰好是第2只被取出的动物的概率为( )
A. B. C. D.
8. 函数的大致图象为( )
A. B.
C. D.
9. 过点作圆的两条切线与圆C分别切于A,B两点,则直线的方程为( )
A. B. C. D.
10. 已知点P为双曲线的左支上一点,O为坐标原点,为双曲线的左,右焦点.且,则双曲线的离心率为( )
A. B. C. D.
11. 已知函数,则下列说法正确的是( )
A 关于直线对称 B. 关于点对称
C 关于点对称 D. 关于直线对称
12. 如图所示,在长方体中,,,则该长方体外接球球心到平面的距离为( )
A B. C. D.
二 填空题:本题共4小题,每小题5分,共20分.
13. 若x,y满足约束条件则的最大值为___________.
14. 已知向量是互相垂直的两个单位向量,若,则___________.
15. 将函数的图象上所有点的横坐标变为原来的倍,纵坐标不变,再将所得图象向右平移个单位,得到函数的图象,当时,值域为___________.
16. 若函数有两个极值点,则实数a的取值范围是___________.
三 解答题:共70分.解答应写出文字说明 证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22 23题为选考题,考生根据要求作答.
17. 在中,角A,B,C的对边分别为a,b,c,.
(1)求;
(2)若,求的面积.
18. 某校新入学的500名高一学生订购校服的尺码柱状图如下图所示:
(1)请根据同学订购校服的尺码柱状图估算该校高一同学的平均身高;
(2)从入学体检可知该校高一男同学平均身高为,女同学平均身高为,请根据体检数据计算出该校高一学生平均身高,并分析(1)中的估算值与由体检数据得出的平均值存在差异的原因.
19. 已知函数在处切线与x轴平行.
(1)求在区间上的最值;
(2)若恰有两个零点,且在上恒成立,求实数c的取值范围.
20. 如图所示,在等腰梯形中,,在等腰梯形中,,将等腰梯形沿所在直线翻折,使得E,F在平面上的射影恰好与A,B重合.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
21. 已知椭圆的焦距为2,分别是C的左右两个焦点,椭圆C上满足的点P有且只有两个.
(1)求椭圆C的标准方程;
(2)若直线l与椭圆C交于A,B两点,且,求证:存在定点Q,使得Q到直线l的距离为定值,并求出这个定值.
22. 平面直角坐标系中,直线l的参数方程为(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设点,直线l交曲线C于A,B两点,求的值.
23. 已知函数.
(1)求满足不等式的实数m的取值范围;
(2)记的最小值为k,若,且,证明:.
芜湖市2021-2022学年高三上学期期末考试
数学(文科)试题卷 答案版
一 选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 集合中的元素个数是( )
A. 0 B. 4 C. 5 D. 6
【答案】B
2. 复数的虚部是( )
A. B. C. D.
【答案】A
3. 徽砚又名歙砚,中国四大名砚之一,是砚史上与端砚齐名珍品.以砚石在古歙州府加工和集散而得名,徽砚始于唐代,据北宋唐积《歙州砚谱》载:婺源砚在唐开元中,猎人叶氏逐兽至长城里,见叠石如城垒状,莹洁可爱,因携之归,刊出成砚,温润大过端溪,此后,徽砚名闻天下,如图所示的徽砚近似底面直径为,高为的圆柱体,则该徽砚的体积为( )
A. B. C. D.
【答案】C
4. 已知,,则p是q( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】B
5. 已知等差数列,公差为,且、、成等比数列,则( )
A. B. C. D.
【答案】D
6. 芜湖市轻轨成为城市发展的新亮点,一号线自2021年11月3日(周三)正式运行以来,给本地居民出行带来极大的便捷.如图为轻轨一号线正式运行后连续若干天的客流量折线图,根据该折线图,下列说法中错误的是( )
A. 一周中周六客流量最大 B. 一周中周一客流量最小
C. 11月13日客流量再创新高 D. 平均客流量大约为5万人
【答案】B
7. 笼子中有2只鸡和2只兔,从中依次随机取出一只动物,直到4只动物全部取出.如果将两只兔子中的某一只起名为“长耳朵”,则“长耳朵”恰好是第2只被取出的动物的概率为( )
A. B. C. D.
【答案】D
8. 函数的大致图象为( )
A. B.
C. D.
【答案】C
9. 过点作圆的两条切线与圆C分别切于A,B两点,则直线的方程为( )
A. B. C. D.
【答案】A
10. 已知点P为双曲线的左支上一点,O为坐标原点,为双曲线的左,右焦点.且,则双曲线的离心率为( )
A. B. C. D.
【答案】B
11. 已知函数,则下列说法正确的是( )
A 关于直线对称 B. 关于点对称
C 关于点对称 D. 关于直线对称
【答案】B
12. 如图所示,在长方体中,,,则该长方体外接球球心到平面的距离为( )
A B. C. D.
【答案】A
二 填空题:本题共4小题,每小题5分,共20分.
13. 若x,y满足约束条件则的最大值为___________.
【答案】5
14. 已知向量是互相垂直的两个单位向量,若,则___________.
【答案】
15. 将函数的图象上所有点的横坐标变为原来的倍,纵坐标不变,再将所得图象向右平移个单位,得到函数的图象,当时,值域为___________.
【答案】
16. 若函数有两个极值点,则实数a的取值范围是___________.
【答案】
三 解答题:共70分.解答应写出文字说明 证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22 23题为选考题,考生根据要求作答.
17. 在中,角A,B,C的对边分别为a,b,c,.
(1)求;
(2)若,求的面积.
【答案】(1);
(2)14.
18. 某校新入学的500名高一学生订购校服的尺码柱状图如下图所示:
(1)请根据同学订购校服的尺码柱状图估算该校高一同学的平均身高;
(2)从入学体检可知该校高一男同学平均身高为,女同学平均身高为,请根据体检数据计算出该校高一学生平均身高,并分析(1)中的估算值与由体检数据得出的平均值存在差异的原因.
【答案】(1)
(2),分析答案见解析
19. 已知函数在处切线与x轴平行.
(1)求在区间上的最值;
(2)若恰有两个零点,且在上恒成立,求实数c的取值范围.
【答案】(1)最小值为,最大值为;
(2).
20. 如图所示,在等腰梯形中,,在等腰梯形中,,将等腰梯形沿所在直线翻折,使得E,F在平面上的射影恰好与A,B重合.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析
(2)
21. 已知椭圆的焦距为2,分别是C的左右两个焦点,椭圆C上满足的点P有且只有两个.
(1)求椭圆C的标准方程;
(2)若直线l与椭圆C交于A,B两点,且,求证:存在定点Q,使得Q到直线l的距离为定值,并求出这个定值.
【答案】(1);
(2)证明见解析,定值.
22. 平面直角坐标系中,直线l的参数方程为(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设点,直线l交曲线C于A,B两点,求的值.
【答案】(1),
(2)
23. 已知函数.
(1)求满足不等式的实数m的取值范围;
(2)记的最小值为k,若,且,证明:.
【答案】(1);
(2)证明见解析.
同课章节目录
