华东师大版七年级下册数学 10.3.2 旋转的特征 教案
文档属性
| 名称 | 华东师大版七年级下册数学 10.3.2 旋转的特征 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 00:00:00 | ||
图片预览


文档简介
《10.3.2旋转的特征》教学设计
一、教材分析
(一)教材地位与作用
10.3.2旋转的特征是华师大版七年级数学下册第十章《轴对称、平移与旋转》第三节的内容,第三节内容主要研究旋转的定义,旋转的特征及其应用,旋转对称图形。本节的主要内容是旋转的特征及其应用。它是在学生学习了图形的旋转的基础上学习的,是后继学习中心对称图形变换的基础,是空间与图形领域的基础知识,在教材中起着承上启下的作用。同时,旋转在日常生活中的应用也非常广泛,利用旋转可以帮助我们解决很多实际问题。
(二)、教学目标
教学目标 知识与技能 1、通过具体实例认识旋转的特征,理解图形中的每一个点都绕着旋转中心按同 一个旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等、对应角相等,图形的形状与大小不变。2、能够按照要求作出简单平面图形旋转后的图形。
数学思考 在发现、探究旋转特征的过程中完成对旋转这一图形变化从直观到抽象,从感性认识到理性认识的转变,发展学生直观想象能力,分析、归纳、抽象概括的思维能力。
解决问题 在了解图形旋转的特征,并进一步应用所掌握的这些特征进行旋转变化的学习过程中,让学生从数学的角度认识现实生活中的现象,增强数学的应用意识。
情感态度与价值观 让学生体验从身边得到数学规律的成就感,在解题中感受生活中数学的存在。通过研究解决问题的方法,培养学生合作交流意识与探究精神。通过学生欣赏、观察、归纳、比较、抽象图形等数学活动,让学生感受数学的严谨性,图形中蕴涵的规律性,提高学生学习数学的热情及大胆探究新知识的创新能力。
(三)、教学重点与难点
重点:理解旋转的基本特征,按照要求作出简单平面图形旋转后的图形。
难点:按照要求作出平面图形旋转后的图形。
二、学情分析
本学段的学生独立思考和探索的愿望和能力有所提高,并能在探索的过程中形成自己的观点,能在倾听别人意见的过程中逐渐完善自己的想法。在此之前学生已经学习了轴对称、平移两种图形变换,并学习了图形的旋转,对图形变换已经具有了一定的认识。存在的困难是空间想象能力不强。
三 、教学方法和手段
使用相关的教学软件:微课宝、几何画板等来完成图形旋转变换的演示。
几何画板对各种图形旋转变换直观形象的演示一方面解决了传统教学中空间想象“不可见”的大难题,巧妙地突破学生学习本节课时空间想象能力差这一难点。另一方面,增加课时容量,同时有利突出重点,分散难点,增加教学条理性、形象性,更好的提高课堂效率,微课宝能及时反馈和评价学生对所学知识的掌握情况。
四、教学过程
创设情景 展示一些自己班级的学生活动的图片,让学生感受在展示这些图片的过程中采用了哪些图形的变化? [设计理念]异校研学交流,没和学生有过接触,通过展示图片并交流,减少隔膜,从生活中的旋转图形出发,激发学生兴趣,引出课题。
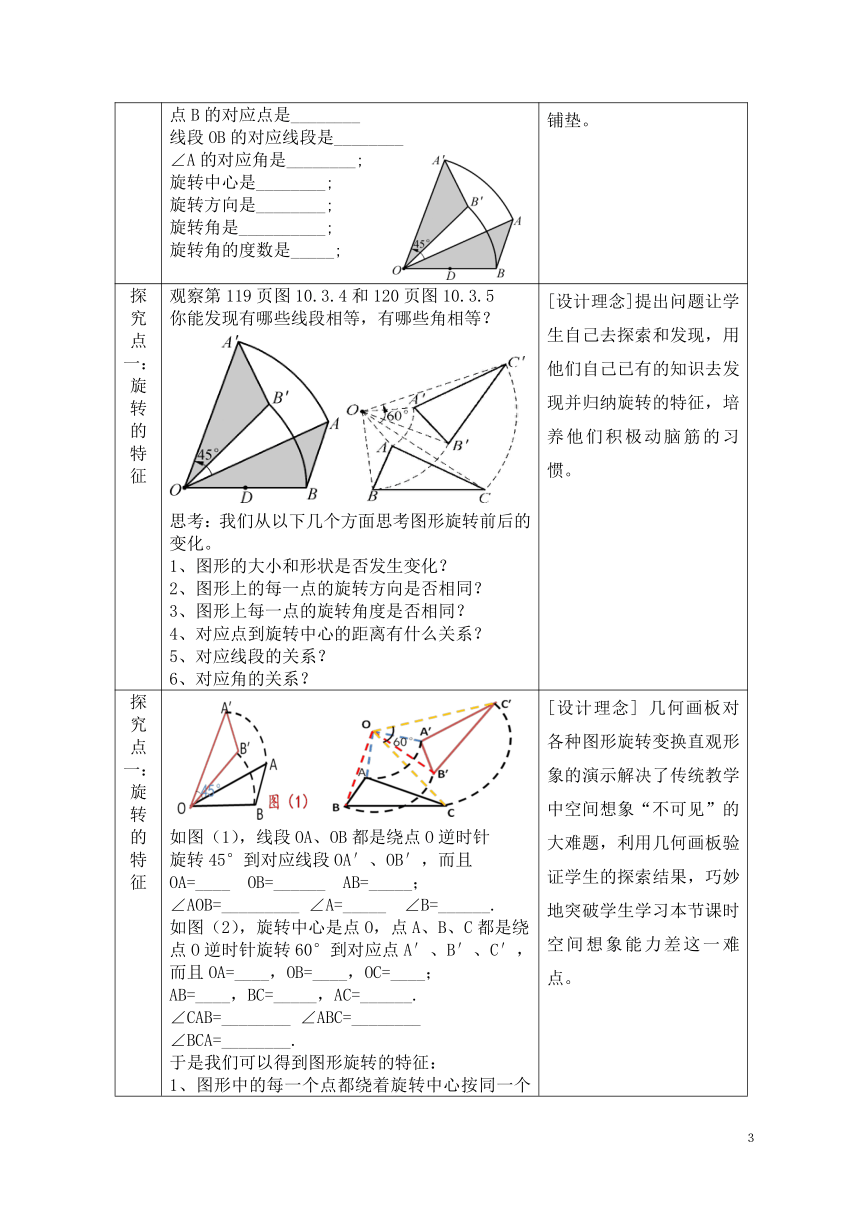
复习旧知 1、什么是旋转?旋转的三个要素是什么?2、如图,△AOB绕点O旋转得到△ A′O B′,则: 点B的对应点是________线段OB的对应线段是________∠A的对应角是________;旋转中心是________;旋转方向是________;旋转角是__________; 旋转角的度数是_____; [设计理念]复习上节课所学的知识,为本节课做好铺垫。
探究点一:旋转的特征 观察第119页图10.3.4和120页图10.3.5你能发现有哪些线段相等,有哪些角相等? 思考:我们从以下几个方面思考图形旋转前后的变化。1、图形的大小和形状是否发生变化?2、图形上的每一点的旋转方向是否相同?3、图形上每一点的旋转角度是否相同?4、对应点到旋转中心的距离有什么关系?5、对应线段的关系?6、对应角的关系? [设计理念]提出问题让学生自己去探索和发现,用他们自己已有的知识去发现并归纳旋转的特征,培养他们积极动脑筋的习惯。
探究点一:旋转的特征 如图(1),线段OA、OB都是绕点O逆时针旋转45°到对应线段OA′、OB′,而且OA=____ OB=______ AB=_____;∠AOB=_________ ∠A=_____ ∠B=______.如图(2),旋转中心是点O,点A、B、C都是绕点O逆时针旋转60°到对应点A′、B′、C′,而且OA=____,OB=____,OC=____; AB=____,BC=_____,AC=______.∠CAB=________ ∠ABC=________ ∠BCA=________.于是我们可以得到图形旋转的特征:1、图形中的每一个点都绕着旋转中心按同一个旋转方向旋转了同样大小的角度。2、对应点到旋转中心的距离相等。3、对应线段相等、对应角相等。4、图形的形状与大小不变。 [设计理念] 几何画板对各种图形旋转变换直观形象的演示解决了传统教学中空间想象“不可见”的大难题,利用几何画板验证学生的探索结果,巧妙地突破学生学习本节课时空间想象能力差这一难点。
例题分析突出重点 例1.如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF. 在这个旋转过程中: (1)旋转中心是什么 (2)经过旋转,点A、B分别移动到什么位置? (3)旋转角是什么? (4)AO与DO的长有什么关系?BO与EO呢? (5)∠AOD与∠BOE有什么大小关系?如图,点D是等边△ABC内一点, 若将△ABD旋转到△ACP, 则旋转中心是 ; 旋转角是 ;= 度,若连结DP, 则△ADP是 三角形. [设计理念] 为了达到突出重点的目的,这里设计了两个例题,让学生在学习了旋转的特征后,学会运用旋转的特征解决有关的问题,在讲解的过程中教师注意和刚才学过的旋转的特征相结合,以加深学生对定义的理解。
探究二:旋转作图 前面我们学习10.1.4设计轴对称图案时,利用轴对称,我们可以设计出许多漂亮的图案。其实,利用旋转,我们也可以设计出漂亮的图案,如图,香港特别行政区区旗中央的紫荆花图案就是利用旋转设计的,它是由其中一个花瓣经过几次旋转得到的 每次旋转了多少度?一个简单的图形经过几次旋转就能变成漂亮的图案,那么如何画出旋转后的图形呢?试画出ABC绕点O逆时针旋转90°后的图形。 [设计理念] 通过观察香港特别行政区区旗中央的紫荆花图案,认识旋转对称图形的美,并尝试画出旋转后的图形,加深对旋转特征的理解,并为学习旋转对称图形做好铺垫。
体会学习数学的价值 欣赏旋转在现实生活中的应用 [设计理念]引导学生用变换的观点解释现实世界中与图形有关的现象,欣赏大千世界的变换美。目的在于引导学生在数学知识和方法的应用中,体会数学的价值,增强用数学的意识,关注数学与现实世界、与其它学科之间的联系。
备用练习 做一做:在下图中,正方形ABCD是正方形EFGH1.如图,△ABO绕点O旋转得到△CDO,在这个旋转过程中:(1)旋转中心是_____,旋转角是____________;(2)经过旋转,点A、B分别移到了__________;(3)若AO=3cm,则CO=__________;(4)若∠AOC=55°,∠AOD=25°,则∠BOD=___,∠BOC=___.2.如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋 转后到达△CAE的位置。问:(1)旋转中心是_____,旋转的度数是____.(2)若∠DCB=20°,则∠CDB=___,∠AEC=___, ∠BAE=___.(3)如果连结DE,那么△DCE是________三角形。, [设计理念] 通过让学生解决蕴含所学知识的实际问题和数学问题将新知识内化入已有的认知结构中。
小结 小结:1、旋转有哪些特征?2、你会找图形旋转前后的对应元素了吗?这节课你理解的最好的地方不明白还需要进一步理解的地方 [设计理念]从知识和能力等方面让学生对所学知识进行概括,相互讨论、回答、补充,共同整理,加深学生对知识的理解,形成知识系统。
作业:感受数学的整体性 拓广探索如图:△ABD、△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的知识说明上述关系成立的理由吗? [设计理念]利用旋转的性质证明三角形全等,从而证明线段相等。体现了《新课标》的整体性原则。教学中有意识、有计划的设计教学活动,引导学生体会数学之间的联系,感受数学的整体性,不断丰富解决问题的策略,提高解决问题的能力。
板书设计
§10.3.2旋转的特征
1、图形中的……
2、对应点……
3、对应线……
4、图形的……
6
6
一、教材分析
(一)教材地位与作用
10.3.2旋转的特征是华师大版七年级数学下册第十章《轴对称、平移与旋转》第三节的内容,第三节内容主要研究旋转的定义,旋转的特征及其应用,旋转对称图形。本节的主要内容是旋转的特征及其应用。它是在学生学习了图形的旋转的基础上学习的,是后继学习中心对称图形变换的基础,是空间与图形领域的基础知识,在教材中起着承上启下的作用。同时,旋转在日常生活中的应用也非常广泛,利用旋转可以帮助我们解决很多实际问题。
(二)、教学目标
教学目标 知识与技能 1、通过具体实例认识旋转的特征,理解图形中的每一个点都绕着旋转中心按同 一个旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等、对应角相等,图形的形状与大小不变。2、能够按照要求作出简单平面图形旋转后的图形。
数学思考 在发现、探究旋转特征的过程中完成对旋转这一图形变化从直观到抽象,从感性认识到理性认识的转变,发展学生直观想象能力,分析、归纳、抽象概括的思维能力。
解决问题 在了解图形旋转的特征,并进一步应用所掌握的这些特征进行旋转变化的学习过程中,让学生从数学的角度认识现实生活中的现象,增强数学的应用意识。
情感态度与价值观 让学生体验从身边得到数学规律的成就感,在解题中感受生活中数学的存在。通过研究解决问题的方法,培养学生合作交流意识与探究精神。通过学生欣赏、观察、归纳、比较、抽象图形等数学活动,让学生感受数学的严谨性,图形中蕴涵的规律性,提高学生学习数学的热情及大胆探究新知识的创新能力。
(三)、教学重点与难点
重点:理解旋转的基本特征,按照要求作出简单平面图形旋转后的图形。
难点:按照要求作出平面图形旋转后的图形。
二、学情分析
本学段的学生独立思考和探索的愿望和能力有所提高,并能在探索的过程中形成自己的观点,能在倾听别人意见的过程中逐渐完善自己的想法。在此之前学生已经学习了轴对称、平移两种图形变换,并学习了图形的旋转,对图形变换已经具有了一定的认识。存在的困难是空间想象能力不强。
三 、教学方法和手段
使用相关的教学软件:微课宝、几何画板等来完成图形旋转变换的演示。
几何画板对各种图形旋转变换直观形象的演示一方面解决了传统教学中空间想象“不可见”的大难题,巧妙地突破学生学习本节课时空间想象能力差这一难点。另一方面,增加课时容量,同时有利突出重点,分散难点,增加教学条理性、形象性,更好的提高课堂效率,微课宝能及时反馈和评价学生对所学知识的掌握情况。
四、教学过程
创设情景 展示一些自己班级的学生活动的图片,让学生感受在展示这些图片的过程中采用了哪些图形的变化? [设计理念]异校研学交流,没和学生有过接触,通过展示图片并交流,减少隔膜,从生活中的旋转图形出发,激发学生兴趣,引出课题。
复习旧知 1、什么是旋转?旋转的三个要素是什么?2、如图,△AOB绕点O旋转得到△ A′O B′,则: 点B的对应点是________线段OB的对应线段是________∠A的对应角是________;旋转中心是________;旋转方向是________;旋转角是__________; 旋转角的度数是_____; [设计理念]复习上节课所学的知识,为本节课做好铺垫。
探究点一:旋转的特征 观察第119页图10.3.4和120页图10.3.5你能发现有哪些线段相等,有哪些角相等? 思考:我们从以下几个方面思考图形旋转前后的变化。1、图形的大小和形状是否发生变化?2、图形上的每一点的旋转方向是否相同?3、图形上每一点的旋转角度是否相同?4、对应点到旋转中心的距离有什么关系?5、对应线段的关系?6、对应角的关系? [设计理念]提出问题让学生自己去探索和发现,用他们自己已有的知识去发现并归纳旋转的特征,培养他们积极动脑筋的习惯。
探究点一:旋转的特征 如图(1),线段OA、OB都是绕点O逆时针旋转45°到对应线段OA′、OB′,而且OA=____ OB=______ AB=_____;∠AOB=_________ ∠A=_____ ∠B=______.如图(2),旋转中心是点O,点A、B、C都是绕点O逆时针旋转60°到对应点A′、B′、C′,而且OA=____,OB=____,OC=____; AB=____,BC=_____,AC=______.∠CAB=________ ∠ABC=________ ∠BCA=________.于是我们可以得到图形旋转的特征:1、图形中的每一个点都绕着旋转中心按同一个旋转方向旋转了同样大小的角度。2、对应点到旋转中心的距离相等。3、对应线段相等、对应角相等。4、图形的形状与大小不变。 [设计理念] 几何画板对各种图形旋转变换直观形象的演示解决了传统教学中空间想象“不可见”的大难题,利用几何画板验证学生的探索结果,巧妙地突破学生学习本节课时空间想象能力差这一难点。
例题分析突出重点 例1.如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF. 在这个旋转过程中: (1)旋转中心是什么 (2)经过旋转,点A、B分别移动到什么位置? (3)旋转角是什么? (4)AO与DO的长有什么关系?BO与EO呢? (5)∠AOD与∠BOE有什么大小关系?如图,点D是等边△ABC内一点, 若将△ABD旋转到△ACP, 则旋转中心是 ; 旋转角是 ;= 度,若连结DP, 则△ADP是 三角形. [设计理念] 为了达到突出重点的目的,这里设计了两个例题,让学生在学习了旋转的特征后,学会运用旋转的特征解决有关的问题,在讲解的过程中教师注意和刚才学过的旋转的特征相结合,以加深学生对定义的理解。
探究二:旋转作图 前面我们学习10.1.4设计轴对称图案时,利用轴对称,我们可以设计出许多漂亮的图案。其实,利用旋转,我们也可以设计出漂亮的图案,如图,香港特别行政区区旗中央的紫荆花图案就是利用旋转设计的,它是由其中一个花瓣经过几次旋转得到的 每次旋转了多少度?一个简单的图形经过几次旋转就能变成漂亮的图案,那么如何画出旋转后的图形呢?试画出ABC绕点O逆时针旋转90°后的图形。 [设计理念] 通过观察香港特别行政区区旗中央的紫荆花图案,认识旋转对称图形的美,并尝试画出旋转后的图形,加深对旋转特征的理解,并为学习旋转对称图形做好铺垫。
体会学习数学的价值 欣赏旋转在现实生活中的应用 [设计理念]引导学生用变换的观点解释现实世界中与图形有关的现象,欣赏大千世界的变换美。目的在于引导学生在数学知识和方法的应用中,体会数学的价值,增强用数学的意识,关注数学与现实世界、与其它学科之间的联系。
备用练习 做一做:在下图中,正方形ABCD是正方形EFGH1.如图,△ABO绕点O旋转得到△CDO,在这个旋转过程中:(1)旋转中心是_____,旋转角是____________;(2)经过旋转,点A、B分别移到了__________;(3)若AO=3cm,则CO=__________;(4)若∠AOC=55°,∠AOD=25°,则∠BOD=___,∠BOC=___.2.如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋 转后到达△CAE的位置。问:(1)旋转中心是_____,旋转的度数是____.(2)若∠DCB=20°,则∠CDB=___,∠AEC=___, ∠BAE=___.(3)如果连结DE,那么△DCE是________三角形。, [设计理念] 通过让学生解决蕴含所学知识的实际问题和数学问题将新知识内化入已有的认知结构中。
小结 小结:1、旋转有哪些特征?2、你会找图形旋转前后的对应元素了吗?这节课你理解的最好的地方不明白还需要进一步理解的地方 [设计理念]从知识和能力等方面让学生对所学知识进行概括,相互讨论、回答、补充,共同整理,加深学生对知识的理解,形成知识系统。
作业:感受数学的整体性 拓广探索如图:△ABD、△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的知识说明上述关系成立的理由吗? [设计理念]利用旋转的性质证明三角形全等,从而证明线段相等。体现了《新课标》的整体性原则。教学中有意识、有计划的设计教学活动,引导学生体会数学之间的联系,感受数学的整体性,不断丰富解决问题的策略,提高解决问题的能力。
板书设计
§10.3.2旋转的特征
1、图形中的……
2、对应点……
3、对应线……
4、图形的……
6
6
