2.3气体的等压变化和等容变化 教案
文档属性
| 名称 | 2.3气体的等压变化和等容变化 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 951.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-12 15:59:29 | ||
图片预览



文档简介
2.3气体的等压变化和等容变化
〖教材分析〗
本课知识主要分为四部分,其中气体的等压、等容变化与前面学习的等温变化,合为气体的三变化。学生可能遇到的问题是气体变化规律解决实际问题,产生这一问题的原因是不会判断气体变化是等温、等容还是等压变化。解决这一问题的方法就是多练,使学生掌握每一种变化情况。结合三个规律的局限性,建立了理想气体模型,进而从微观上解释了气体实验定律。
〖教学目标与核心素养〗
物理观念∶能建立等压过程、等容过程的物理观念,理解这两个过程状态参量的变化。
科学思维∶知道理想气体是一种理想化的物理模型,现实中并不存在,具有建构“理想化的物理模型”的意识。
科学探究:具有与他人交流成果,讨论问题的意识。
科学态度与责任∶理解物理概念的建立的过程和规律;感悟自然界的统一、和谐美;认识到气体实验的规律可以从微观解释,也可以从宏观来感受。
〖教学重难点〗
教学重点:盖—吕萨克和查理定律的理解和计算。
教学难点:盖—吕萨克和查理定律的理解和计算,以及图像问题。
〖教学准备〗
多媒体课件等。
〖教学过程〗
一、新课引入
烧瓶上通过橡胶塞连接一根玻璃管,向玻璃管中注入一段水柱。用手捂住烧瓶,会观察到水柱缓慢向外移动,这说明了什么
实验表明:温度升高时,为了保持气体的压强不变的情况下,气体的体积要随温度的升高而增大。
二、新课教学
(一)气体的等压变化
1.等压变化的概念
温度,压强和体积是气体的三个状态参量,对于一定质量的某种气体,让温度不变,研究压强与体积的变化关系,就是之前学习的等温变化,那如果换成压强不变,研究体积随温度的变化,那就是等压变化。即
一定质量的某种气体,在压强不变时,体积随温度变化的过程叫作气体的等压变化。
实验表面,在V—T图像中,等压线是一条过原点的直线。对于一定质量的气体,温度不变时,压强越大,体积就越小。
2.盖—吕萨克定律
法国科学家盖—吕萨克通过研究发现这一线性关系。得出结论:
一定质量的某种气体,在压强不变的情况下,其体积与热力学温度成正比。
V=CT或
注意
①公式的T是热力学温度。
②适用条件:压强不太大,温度不太低;气体的质量和压强都不变。
③V1T1和V2T2分别表示一定质量的气体在等压变化时,两个不同状态下的体积和热力学温度。
课堂练习
例1:一容器中装有某种气体,且容器上有一个小口与外界大气相通,原来容器内的温度为27℃,若把它加热到127℃,从容器中溢出的空气质量是原来质量的多少倍呢?
分析:图中容器上有一个小口,与外界大气相通,说明容器内外压强始终相同,可以看作是等压变化。那咱根据这个公式,只要把V1T1和V2T2都搞清楚不就好了吗。
解:等压变化过程
初态: P1=P0 V1=V T1=27+273=300K
末态:P2=P0 V2=? T2=127+273=400K
根据:
代入数据得:
解得:
这个体积怎么比容器还要大呢?别忘了这里有个小孔,气体是一直在溢出的,所以你不能只考虑容器内的气体,咱可以假设在这里加了一层无形的膜。这部分就是溢出的气体在容器内的体积是立外面就还剩下1/3V。但你要当心,最后求得是溢出的空气质量,这里溢出的气体是1/3V,整个气体体积是4/3V才对,所以溢出的部分只占总体及大1/4 那质量就也是1/4,这才是正确答案。
(二)气体的等容变化
1.等容变化的概念
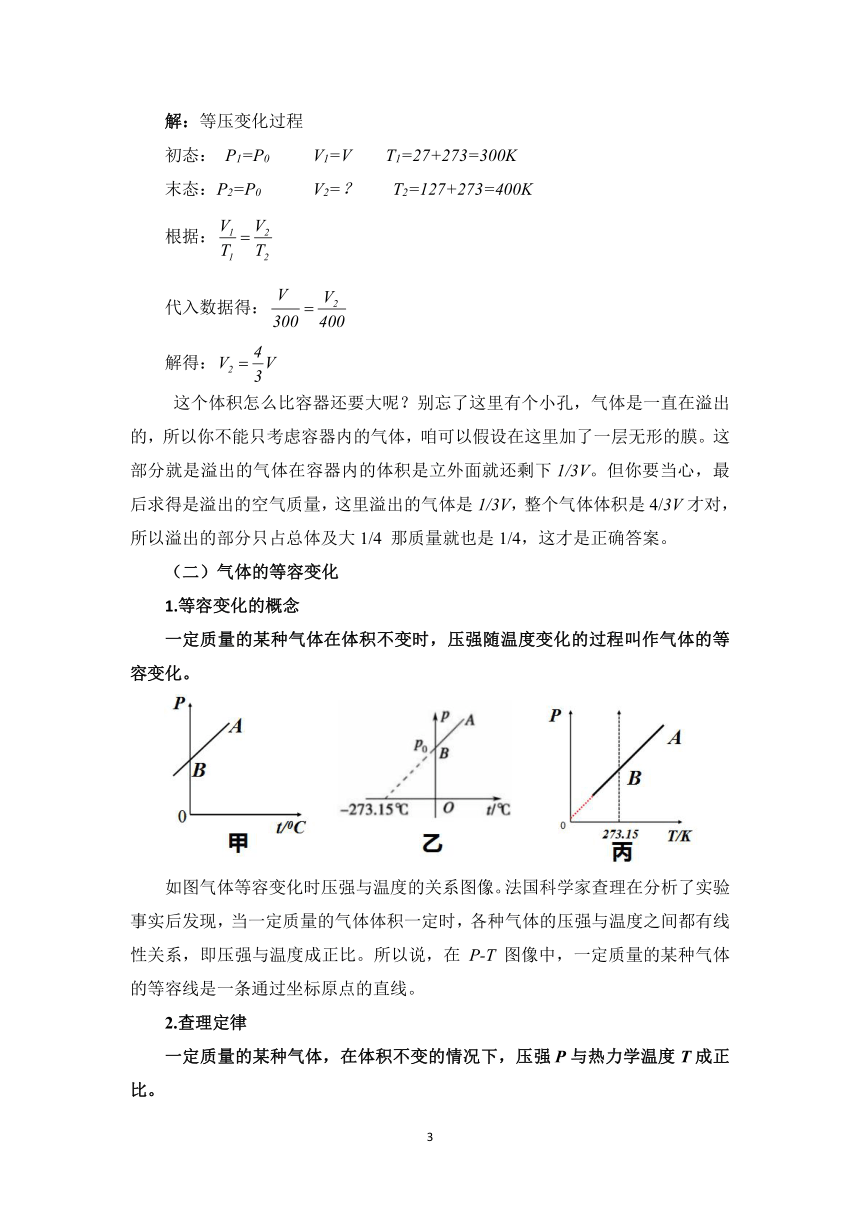
一定质量的某种气体在体积不变时,压强随温度变化的过程叫作气体的等容变化。
如图气体等容变化时压强与温度的关系图像。法国科学家查理在分析了实验事实后发现,当一定质量的气体体积一定时,各种气体的压强与温度之间都有线性关系,即压强与温度成正比。所以说,在 P-T 图像中,一定质量的某种气体的等容线是一条通过坐标原点的直线。
2.查理定律
一定质量的某种气体,在体积不变的情况下,压强P与热力学温度T成正比。
P=CT或
注意
①公式的T是热力学温度。
②适用条件:压强不太大,温度不太低;气体的质量和体积都不变。
③P1T1和P2T2分别表示一定质量的气体在等容变化时,两个不同状态下的压强和热力学温度。
课堂练习
例2:某种气体的压强为2×105Pa,体积为1m3,温度为200K。它经过等温过程后体积变为2m3。随后又经过等容过程,温度变为300K,求此时气体的压强?
分析:分别按等温变化和等容变化来求解。
解:等温变化过程
初态: P1=2×105Pa V1=1m3 T1=200K
末态:P2= V2=2m T2=200K
根据:p1V1=p2V2
代入数据得:2×105×1=P2×2
解得:P2=105Pa
等容变化过程
初态: P2=105Pa V2=2m3 T2=200K
末态: P3=? V3=2m3 T3=300K
根据∶
代入数据得:
解得:P3=1.5×105Pa
思考:分别学习波意耳定律,查理定律和盖—吕萨克定律 分别都有等温、等容和等压变化,不知你是否还记得,三条定律都只在压强不太大,温度不太低时成立。但是当压强很大,或者温度很低时,结果会怎样呢?
举例子说明
初态: P1=P0 V1=1m3 T1=273K
令温度不变,压强增大
末态:P2=500P0 V2=? T2=273K
根据:p1V1=p2V2
代入数据得:
但实际测量的结果并非如此,而是1.36/500m 。与实际有偏离,另外两个定律也存在这样的问题。
疑惑:压强很大、温度很低,结果会偏离的问题,这不就给科学研究带来了麻烦吗?
(三)理想气体
建立理想化模型:可以假设存在这样一种气体。
在任何温度,任何压强下都遵从气体实验定律,就叫他理想气体。
从微观角度来看看理想气体,气体分子被看成一个个质点,忽略了分子的体积,也忽略他们之间的吸引和排斥,相当于忽略了分子势能。所以
①理想气体的内能=分子动能之和(只与温度有关)。
②它是一种理想模型和实际气体近似。
③实际气体压强不太大,温度不太低,就可以看做理想气体。
拓展学习
理想气体的状态方程:描述一定质量的某种理想气,体状态的参量有三个,即压强p、体积V和温度T。
课本例题的解法:
初态: P1=2×105Pa V1=1m3 T2=200K
末态: P2=? V2=2m3 T3=300K
根据:
解得:P2=1.5×105Pa
结果也是一样的,而且更快,省去了很多中间环节。
(五)气体实验定律的微观解释
①波意耳定律:一定质量的某种气体,在温度不变的情况下,压强P与体积V成反比
温度不变→不变
那么V↓→分子密集程度↑→P↑。
②盖—吕萨克定律:一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比。
T↑→↑→P↑。
为了抑制压强的增大,只能减少分子密集程度→V↑
③查理定律:一定质量的某种气体,在体积不变的情况下,压强P与热力学温度T成正比。
体积不变→分子密集程度不变。
T↑→↑→P↑。
从微观角度解释了这三个气体定律,它给了咱新的分析问题的视角,你理解就行,不要死记硬背。
科学方法:理想模型
课堂练习
例3:如图所示,一定质量的理想气体由状态A,沿平行于纵轴的直线变化到状态B,则它的状态变化过程是( )
气体温度不变
气体的内能增加
气体分子的平均速率减小
气体分子在单位时间与器壁单位面积碰撞的次数不变
解析:这是一个压强体积图,那平行于纵轴的直线,就意味着体积不变。从A到B压强增大,所以这也是一个等容升压的过程。根据查理定律,此时压强与热力学温度成正比,所以压强增大,温度应该升高啦。哪A选项说的气体的温度不变就是错误的。看B选项,气体的内能增加,因为理想气体的内能等于分子动能,温度升高,气体分子的平均速率增大,所以平均动能增大,内能当然也增大,所以B是正确,C选项错的。最后看D选项,气体分子在单位时间内与器壁单位面积碰撞的次数不变,刚才说了气体分子的平均速率增大,在分子密集程度不变的情况下,单位时间内与器壁的碰撞次数肯定增大,那这样的话地也是错的。综上所述,正确答案选B。
例4:盛有氧气的钢瓶,在17℃的室内测得氧气的压强是9.31×106Pa。当钢瓶到-13℃的工地上时,瓶内氧气的压强变为8.15×106Pa。钢瓶是不是漏气 为什么?
解:以钢瓶内气体为研究对象,等容变化过程。
初态: P1=9.31×106Pa V1=V T1=17+273.15=290.15K
末态: P2=? V2=V T2=-13+273.15=260.15K
根据:
代入数据得:
解得:P2=8.35×106Pa
比测量值大,说明漏气了。
〖板书设计〗
2.3气体的等压变化和等容变化
一、气体的等压变化
盖—吕萨克定律∶一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比。
二、气体的等容变化
查理定律∶一定质量的某种气体,在体积不变的情况下,压强P与热力学温度T成正比。
三、理想气体:在任何温度,任何压强下都遵从气体实验定律。
①理想气体的内能=分子动能之和(只与温度有关)
②它是一种理想模型和实际气体近似
③实际气体压强不太大,温度不太低,就可以看做理想气体
四、气体实验定律的微观解释
〖教学反思〗
气体的等压和等容变化,它们基本上介于宏观喝微观之间,可以从微观去解释,又可以从宏观上直接感受。这对于学生的学习是由一定的帮助的,但是也可能使学生对知识变得更加模糊。理想气体的转态方程作为一个拓展学习内容,但是在课本的例题又出现了理想气体的转态方程,那么这个内容的讲解可以把例题的讲解的方法放到拓展学习再讲。例题的讲解还是按老办法分两个过程去讲解就好了。
(
1
)
〖教材分析〗
本课知识主要分为四部分,其中气体的等压、等容变化与前面学习的等温变化,合为气体的三变化。学生可能遇到的问题是气体变化规律解决实际问题,产生这一问题的原因是不会判断气体变化是等温、等容还是等压变化。解决这一问题的方法就是多练,使学生掌握每一种变化情况。结合三个规律的局限性,建立了理想气体模型,进而从微观上解释了气体实验定律。
〖教学目标与核心素养〗
物理观念∶能建立等压过程、等容过程的物理观念,理解这两个过程状态参量的变化。
科学思维∶知道理想气体是一种理想化的物理模型,现实中并不存在,具有建构“理想化的物理模型”的意识。
科学探究:具有与他人交流成果,讨论问题的意识。
科学态度与责任∶理解物理概念的建立的过程和规律;感悟自然界的统一、和谐美;认识到气体实验的规律可以从微观解释,也可以从宏观来感受。
〖教学重难点〗
教学重点:盖—吕萨克和查理定律的理解和计算。
教学难点:盖—吕萨克和查理定律的理解和计算,以及图像问题。
〖教学准备〗
多媒体课件等。
〖教学过程〗
一、新课引入
烧瓶上通过橡胶塞连接一根玻璃管,向玻璃管中注入一段水柱。用手捂住烧瓶,会观察到水柱缓慢向外移动,这说明了什么
实验表明:温度升高时,为了保持气体的压强不变的情况下,气体的体积要随温度的升高而增大。
二、新课教学
(一)气体的等压变化
1.等压变化的概念
温度,压强和体积是气体的三个状态参量,对于一定质量的某种气体,让温度不变,研究压强与体积的变化关系,就是之前学习的等温变化,那如果换成压强不变,研究体积随温度的变化,那就是等压变化。即
一定质量的某种气体,在压强不变时,体积随温度变化的过程叫作气体的等压变化。
实验表面,在V—T图像中,等压线是一条过原点的直线。对于一定质量的气体,温度不变时,压强越大,体积就越小。
2.盖—吕萨克定律
法国科学家盖—吕萨克通过研究发现这一线性关系。得出结论:
一定质量的某种气体,在压强不变的情况下,其体积与热力学温度成正比。
V=CT或
注意
①公式的T是热力学温度。
②适用条件:压强不太大,温度不太低;气体的质量和压强都不变。
③V1T1和V2T2分别表示一定质量的气体在等压变化时,两个不同状态下的体积和热力学温度。
课堂练习
例1:一容器中装有某种气体,且容器上有一个小口与外界大气相通,原来容器内的温度为27℃,若把它加热到127℃,从容器中溢出的空气质量是原来质量的多少倍呢?
分析:图中容器上有一个小口,与外界大气相通,说明容器内外压强始终相同,可以看作是等压变化。那咱根据这个公式,只要把V1T1和V2T2都搞清楚不就好了吗。
解:等压变化过程
初态: P1=P0 V1=V T1=27+273=300K
末态:P2=P0 V2=? T2=127+273=400K
根据:
代入数据得:
解得:
这个体积怎么比容器还要大呢?别忘了这里有个小孔,气体是一直在溢出的,所以你不能只考虑容器内的气体,咱可以假设在这里加了一层无形的膜。这部分就是溢出的气体在容器内的体积是立外面就还剩下1/3V。但你要当心,最后求得是溢出的空气质量,这里溢出的气体是1/3V,整个气体体积是4/3V才对,所以溢出的部分只占总体及大1/4 那质量就也是1/4,这才是正确答案。
(二)气体的等容变化
1.等容变化的概念
一定质量的某种气体在体积不变时,压强随温度变化的过程叫作气体的等容变化。
如图气体等容变化时压强与温度的关系图像。法国科学家查理在分析了实验事实后发现,当一定质量的气体体积一定时,各种气体的压强与温度之间都有线性关系,即压强与温度成正比。所以说,在 P-T 图像中,一定质量的某种气体的等容线是一条通过坐标原点的直线。
2.查理定律
一定质量的某种气体,在体积不变的情况下,压强P与热力学温度T成正比。
P=CT或
注意
①公式的T是热力学温度。
②适用条件:压强不太大,温度不太低;气体的质量和体积都不变。
③P1T1和P2T2分别表示一定质量的气体在等容变化时,两个不同状态下的压强和热力学温度。
课堂练习
例2:某种气体的压强为2×105Pa,体积为1m3,温度为200K。它经过等温过程后体积变为2m3。随后又经过等容过程,温度变为300K,求此时气体的压强?
分析:分别按等温变化和等容变化来求解。
解:等温变化过程
初态: P1=2×105Pa V1=1m3 T1=200K
末态:P2= V2=2m T2=200K
根据:p1V1=p2V2
代入数据得:2×105×1=P2×2
解得:P2=105Pa
等容变化过程
初态: P2=105Pa V2=2m3 T2=200K
末态: P3=? V3=2m3 T3=300K
根据∶
代入数据得:
解得:P3=1.5×105Pa
思考:分别学习波意耳定律,查理定律和盖—吕萨克定律 分别都有等温、等容和等压变化,不知你是否还记得,三条定律都只在压强不太大,温度不太低时成立。但是当压强很大,或者温度很低时,结果会怎样呢?
举例子说明
初态: P1=P0 V1=1m3 T1=273K
令温度不变,压强增大
末态:P2=500P0 V2=? T2=273K
根据:p1V1=p2V2
代入数据得:
但实际测量的结果并非如此,而是1.36/500m 。与实际有偏离,另外两个定律也存在这样的问题。
疑惑:压强很大、温度很低,结果会偏离的问题,这不就给科学研究带来了麻烦吗?
(三)理想气体
建立理想化模型:可以假设存在这样一种气体。
在任何温度,任何压强下都遵从气体实验定律,就叫他理想气体。
从微观角度来看看理想气体,气体分子被看成一个个质点,忽略了分子的体积,也忽略他们之间的吸引和排斥,相当于忽略了分子势能。所以
①理想气体的内能=分子动能之和(只与温度有关)。
②它是一种理想模型和实际气体近似。
③实际气体压强不太大,温度不太低,就可以看做理想气体。
拓展学习
理想气体的状态方程:描述一定质量的某种理想气,体状态的参量有三个,即压强p、体积V和温度T。
课本例题的解法:
初态: P1=2×105Pa V1=1m3 T2=200K
末态: P2=? V2=2m3 T3=300K
根据:
解得:P2=1.5×105Pa
结果也是一样的,而且更快,省去了很多中间环节。
(五)气体实验定律的微观解释
①波意耳定律:一定质量的某种气体,在温度不变的情况下,压强P与体积V成反比
温度不变→不变
那么V↓→分子密集程度↑→P↑。
②盖—吕萨克定律:一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比。
T↑→↑→P↑。
为了抑制压强的增大,只能减少分子密集程度→V↑
③查理定律:一定质量的某种气体,在体积不变的情况下,压强P与热力学温度T成正比。
体积不变→分子密集程度不变。
T↑→↑→P↑。
从微观角度解释了这三个气体定律,它给了咱新的分析问题的视角,你理解就行,不要死记硬背。
科学方法:理想模型
课堂练习
例3:如图所示,一定质量的理想气体由状态A,沿平行于纵轴的直线变化到状态B,则它的状态变化过程是( )
气体温度不变
气体的内能增加
气体分子的平均速率减小
气体分子在单位时间与器壁单位面积碰撞的次数不变
解析:这是一个压强体积图,那平行于纵轴的直线,就意味着体积不变。从A到B压强增大,所以这也是一个等容升压的过程。根据查理定律,此时压强与热力学温度成正比,所以压强增大,温度应该升高啦。哪A选项说的气体的温度不变就是错误的。看B选项,气体的内能增加,因为理想气体的内能等于分子动能,温度升高,气体分子的平均速率增大,所以平均动能增大,内能当然也增大,所以B是正确,C选项错的。最后看D选项,气体分子在单位时间内与器壁单位面积碰撞的次数不变,刚才说了气体分子的平均速率增大,在分子密集程度不变的情况下,单位时间内与器壁的碰撞次数肯定增大,那这样的话地也是错的。综上所述,正确答案选B。
例4:盛有氧气的钢瓶,在17℃的室内测得氧气的压强是9.31×106Pa。当钢瓶到-13℃的工地上时,瓶内氧气的压强变为8.15×106Pa。钢瓶是不是漏气 为什么?
解:以钢瓶内气体为研究对象,等容变化过程。
初态: P1=9.31×106Pa V1=V T1=17+273.15=290.15K
末态: P2=? V2=V T2=-13+273.15=260.15K
根据:
代入数据得:
解得:P2=8.35×106Pa
比测量值大,说明漏气了。
〖板书设计〗
2.3气体的等压变化和等容变化
一、气体的等压变化
盖—吕萨克定律∶一定质量的某种气体,在压强不变的情况下,其体积V与热力学温度T成正比。
二、气体的等容变化
查理定律∶一定质量的某种气体,在体积不变的情况下,压强P与热力学温度T成正比。
三、理想气体:在任何温度,任何压强下都遵从气体实验定律。
①理想气体的内能=分子动能之和(只与温度有关)
②它是一种理想模型和实际气体近似
③实际气体压强不太大,温度不太低,就可以看做理想气体
四、气体实验定律的微观解释
〖教学反思〗
气体的等压和等容变化,它们基本上介于宏观喝微观之间,可以从微观去解释,又可以从宏观上直接感受。这对于学生的学习是由一定的帮助的,但是也可能使学生对知识变得更加模糊。理想气体的转态方程作为一个拓展学习内容,但是在课本的例题又出现了理想气体的转态方程,那么这个内容的讲解可以把例题的讲解的方法放到拓展学习再讲。例题的讲解还是按老办法分两个过程去讲解就好了。
(
1
)
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
