§12.1轴对称(3)课堂练习学案
文档属性
| 名称 | §12.1轴对称(3)课堂练习学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 34.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-28 00:00:00 | ||
图片预览

文档简介
§12.1轴对称(3)课堂练习学案
一、自主学习
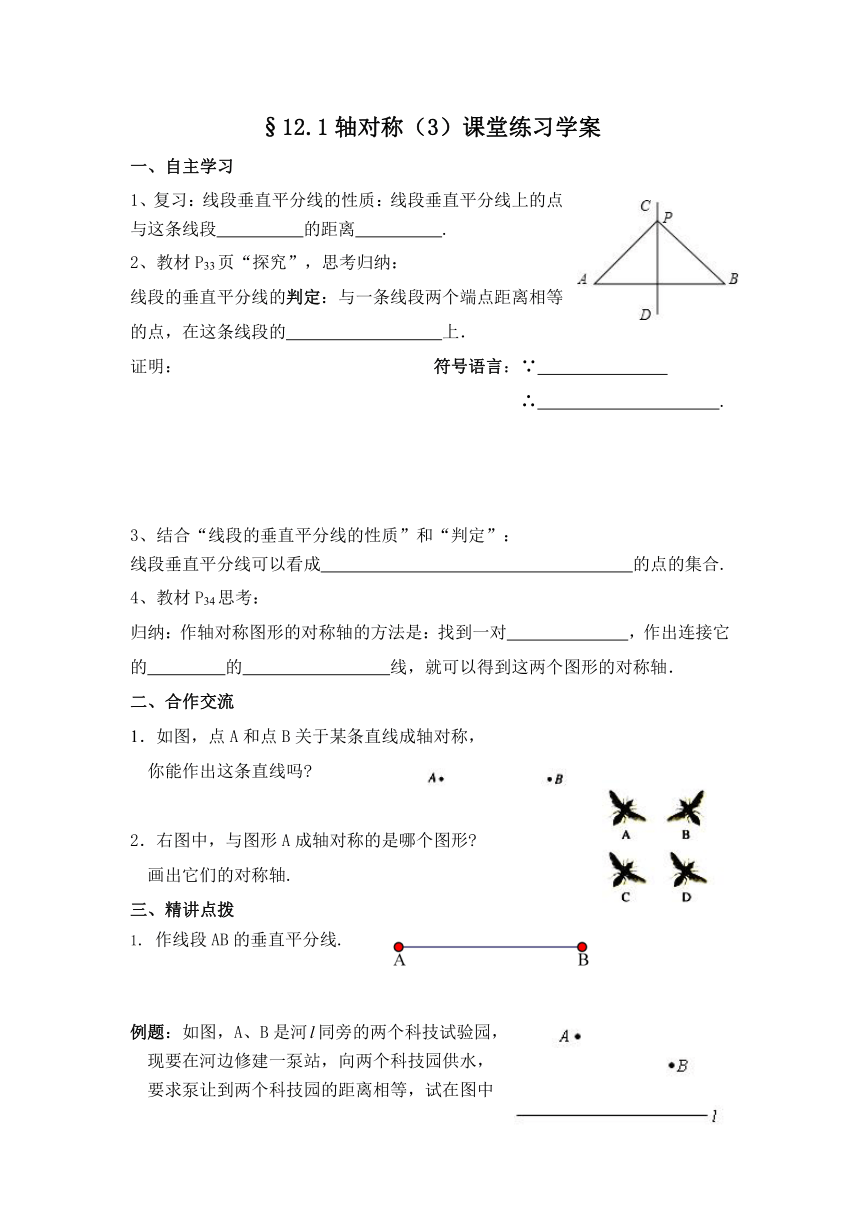
1、复习:线段垂直平分线的性质:线段垂直平分线上的点 与这条线段 的距离 .
2、教材P33页“探究”,思考归纳:
线段的垂直平分线的判定:与一条线段两个端点距离相等的点,在这条线段的 上.
证明: 符号语言:∵
∴ .
3、结合“线段的垂直平分线的性质”和“判定”:
线段垂直平分线可以看成 的点的集合.
4、教材P34思考:
归纳:作轴对称图形的对称轴的方法是:找到一对 ,作出连接它 的 的 线,就可以得到这两个图形的对称轴.
二、合作交流
1.如图,点A和点B关于某条直线成轴对称,
你能作出这条直线吗?
2.右图中,与图形A成轴对称的是哪个图形?
画出它们的对称轴.
三、精讲点拨
1. 作线段AB的垂直平分线.
例题:如图,A、B是河同旁的两个科技试验园,
现要在河边修建一泵站,向两个科技园供水,
要求泵让到两个科技园的距离相等,试在图中
确定泵站的位置.
课堂练习:
1.点P是△ABC内的一点,且满足PA=PB=PC,则点P是△ABC的( )
A.三条角平分线的交点 B.三条中线的交点
C.三条高线的交点 D.三边垂直平分线的交点
2、如图,∠AOB内一点P,P1,P2分别P是关于OA、OB
的对称点,P1P2交OA于M,交OB于N,若P1P2=5cm,
则△PMN的周长是( )
A.3cm B.4cm
C.5cm D.6cm
3、在四边形ABCD中,AB=AD,BC边的垂直平分线经过点A.
求证:点A在CD的垂直平分线上.
4、如图,AD是△ABC的∠BAC的平分线,DE、DF分别是△ABD和△ACD的高.
求证:AD是EF的垂直平分线.
5、如图:求作一点P,使PM=PN,并且使点P
到∠AOB的两边的距离相等.
一、自主学习
1、复习:线段垂直平分线的性质:线段垂直平分线上的点 与这条线段 的距离 .
2、教材P33页“探究”,思考归纳:
线段的垂直平分线的判定:与一条线段两个端点距离相等的点,在这条线段的 上.
证明: 符号语言:∵
∴ .
3、结合“线段的垂直平分线的性质”和“判定”:
线段垂直平分线可以看成 的点的集合.
4、教材P34思考:
归纳:作轴对称图形的对称轴的方法是:找到一对 ,作出连接它 的 的 线,就可以得到这两个图形的对称轴.
二、合作交流
1.如图,点A和点B关于某条直线成轴对称,
你能作出这条直线吗?
2.右图中,与图形A成轴对称的是哪个图形?
画出它们的对称轴.
三、精讲点拨
1. 作线段AB的垂直平分线.
例题:如图,A、B是河同旁的两个科技试验园,
现要在河边修建一泵站,向两个科技园供水,
要求泵让到两个科技园的距离相等,试在图中
确定泵站的位置.
课堂练习:
1.点P是△ABC内的一点,且满足PA=PB=PC,则点P是△ABC的( )
A.三条角平分线的交点 B.三条中线的交点
C.三条高线的交点 D.三边垂直平分线的交点
2、如图,∠AOB内一点P,P1,P2分别P是关于OA、OB
的对称点,P1P2交OA于M,交OB于N,若P1P2=5cm,
则△PMN的周长是( )
A.3cm B.4cm
C.5cm D.6cm
3、在四边形ABCD中,AB=AD,BC边的垂直平分线经过点A.
求证:点A在CD的垂直平分线上.
4、如图,AD是△ABC的∠BAC的平分线,DE、DF分别是△ABD和△ACD的高.
求证:AD是EF的垂直平分线.
5、如图:求作一点P,使PM=PN,并且使点P
到∠AOB的两边的距离相等.
