人教版数学七下9.3一元一次不等式组 课件(共17张)
文档属性
| 名称 | 人教版数学七下9.3一元一次不等式组 课件(共17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 241.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 20:20:43 | ||
图片预览





文档简介
(共17张PPT)
七年级数学·下 新课标[人]
第九章 不等式与不等式组
一元一次不等式组
思考 用每分钟可抽30吨水的抽水机来抽取污水,积存的污水超过1200吨而不足1500吨,那么将污水抽完所用的时间的范围是什么?
设用x min将污水抽完,则x应该满足什么样的式子呢?
30x>1200
30x<1500
{
类似于方程组,把这两个不等式合起来,组成一个一元一次不等式组。
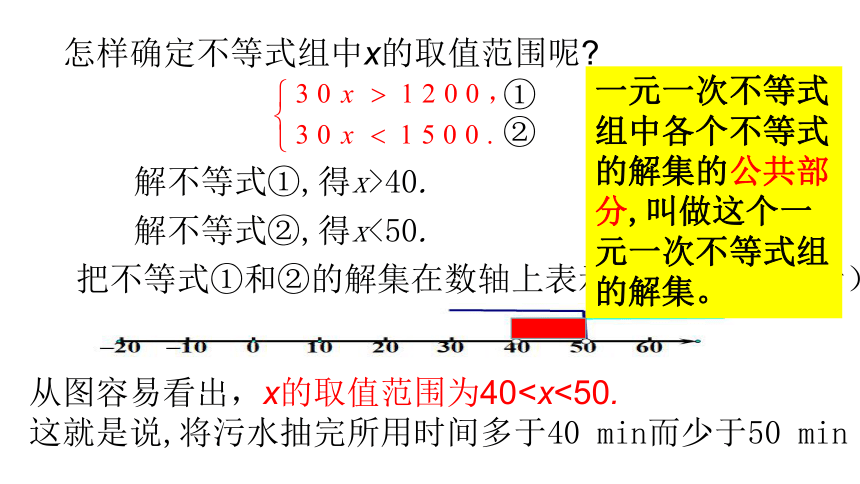
怎样确定不等式组中x的取值范围呢
解不等式①,得x>40.
解不等式②,得x<50.
把不等式①和②的解集在数轴上表示出来.(如图所示)
①
②
从图容易看出,x的取值范围为40这就是说,将污水抽完所用时间多于40 min而少于50 min
一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集。
利用数轴来确定下列不等式组的解集:
偶数组
奇数组
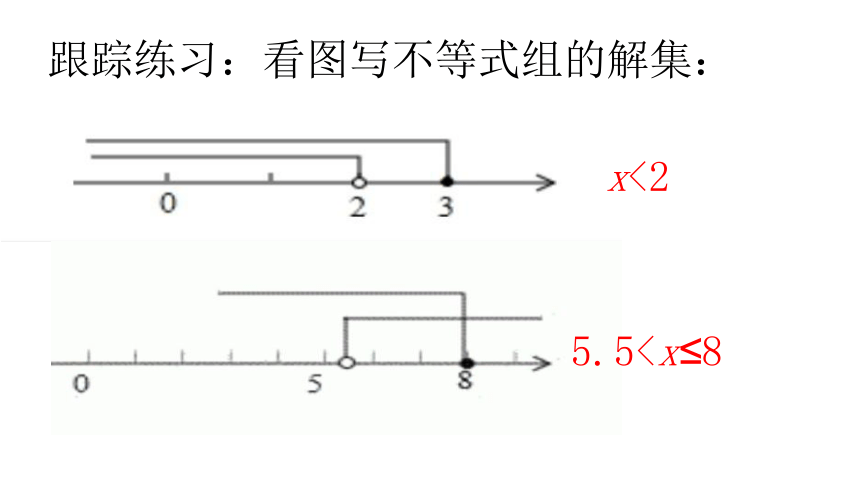
跟踪练习:看图写不等式组的解集:
5.5x<2
0 2 3
例:解下列不等式组
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
⑴
②
①
所以不等式组的解集:
求不等式组的解集的过程叫做解不等式组
2.利用数轴,求出这些不等式解集的公共部分;
解下列不等式组
①
②
(2)
归纳解一元一次不等式组的步骤:
1.求出不等式组中各个不等式的解集;
3.写出不等式组的解集。
【问题1】为了响应市创建卫生城市活动,某小区物业准备对小区内的一个被污染的水池进行整改。估计水池里的污水超过1200t而不足1500t,可供使用的是每分钟可抽水30t的抽水机,你能帮忙算算将污水抽取完所用的时间的范围是多少吗?
情境感知
思考:1、这个问题中的数量都有哪些?
2、这些数量之间是等量关系吗?或者是?
3、若我们设x min将污水抽完,则x应该满足什么样的式子呢?
30 x <1500
类似于方程组,把这两个不等式合起来,组成一个一元一次不等式组,记作
30 x >1200
30 x >1200
30 x <1500
【问题2】什么是方程组的解?类似于方程组的解,你能说说不等式组的解集吗?
一般地,几个不等式的解集的公共部分,叫做这几个 不等式组成的不等式组的解集
请利用前面学习的解不等式的方法分别解出两个不等式,并把各自的解集表示在同一条数轴上!
0
40
50
x <50
x >40
类比归纳
40< x <50
解法探究
【问题3】利用数轴来确定不等式组的解集:
x >3
x >-1
(1)
∴不等式组的解集是: x >3
x < 3
x <-1
(2)
∴不等式组的解集是: x <-1
x < 3
x >-1
(3)
∴不等式组的解集是: -1< x <3
x > 3
x <-1
(4)
3
-1
3
-1
3
-1
3
-1
∴不等式组的解集是: 无解
例题演示
2x-1> x +1 , ①
x+8 <4x-1 ; ②
(1)
2x+3≥ x +11 , ①
-1<2-x . ②
(2)
2x+5
3
【问题4】解下列不等式组:
2
3
例题演示
解:(1)解不等式①得x>2.
解不等式②得x>3.
把不等式① 和②的解集在数轴上表示出来:
从图中可以找到两个不等式解集的公共部分,得不等式组的解集是: x >3.
同学们自己完成第二题.
2x-1> x +1 , ①
x+8 <4x-1 ; ②
(1)
例题演示
x取哪些整数值时,不等式5x+2>3(x-1)
与 x-1≤7 - x 都成立?
分析:要求x的整数解,需先确定x的取值范围(即求出不等式组的解集),解集中的整数就是x可取的整数值.
本节课你有什么收获?
类似于方程组,把这两个不等式合起来,组成一个一元一次不等式组。
归纳解一元一次不等式组的步骤:
1.求出不等式组中各个不等式的解集;
2.利用数轴,求出这些不等式解集的公共部分;
3.写出不等式组的解集。
求不等式组的解集的过程叫做解不等式组
一元一次不等式组中各不等式解集的公共部分叫作一元一次不等式组的解集
1.不等式组
的解集为( )
.
B.
C.
D.无解
A.
学以致用
2.已知不等式①,②,③的解集在数轴上的表示如图所示,则它们的公共部分的解集是( )
A.-1≤x<3 B.1≤x<3 C.-1≤x<1 D.无解
B
B
3、解不等式组
解不等式
得____,
解不等式
得____,
所以不等式组的解集是___ __.
4、不等式组
的正整数解是( )
A.0和1 B.2和3 C.1和3 D.1和2
D
-3<x≤0
x≤0
x>-3
谢谢聆听
七年级数学·下 新课标[人]
第九章 不等式与不等式组
一元一次不等式组
思考 用每分钟可抽30吨水的抽水机来抽取污水,积存的污水超过1200吨而不足1500吨,那么将污水抽完所用的时间的范围是什么?
设用x min将污水抽完,则x应该满足什么样的式子呢?
30x>1200
30x<1500
{
类似于方程组,把这两个不等式合起来,组成一个一元一次不等式组。
怎样确定不等式组中x的取值范围呢
解不等式①,得x>40.
解不等式②,得x<50.
把不等式①和②的解集在数轴上表示出来.(如图所示)
①
②
从图容易看出,x的取值范围为40
一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集。
利用数轴来确定下列不等式组的解集:
偶数组
奇数组
跟踪练习:看图写不等式组的解集:
5.5
0 2 3
例:解下列不等式组
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
⑴
②
①
所以不等式组的解集:
求不等式组的解集的过程叫做解不等式组
2.利用数轴,求出这些不等式解集的公共部分;
解下列不等式组
①
②
(2)
归纳解一元一次不等式组的步骤:
1.求出不等式组中各个不等式的解集;
3.写出不等式组的解集。
【问题1】为了响应市创建卫生城市活动,某小区物业准备对小区内的一个被污染的水池进行整改。估计水池里的污水超过1200t而不足1500t,可供使用的是每分钟可抽水30t的抽水机,你能帮忙算算将污水抽取完所用的时间的范围是多少吗?
情境感知
思考:1、这个问题中的数量都有哪些?
2、这些数量之间是等量关系吗?或者是?
3、若我们设x min将污水抽完,则x应该满足什么样的式子呢?
30 x <1500
类似于方程组,把这两个不等式合起来,组成一个一元一次不等式组,记作
30 x >1200
30 x >1200
30 x <1500
【问题2】什么是方程组的解?类似于方程组的解,你能说说不等式组的解集吗?
一般地,几个不等式的解集的公共部分,叫做这几个 不等式组成的不等式组的解集
请利用前面学习的解不等式的方法分别解出两个不等式,并把各自的解集表示在同一条数轴上!
0
40
50
x <50
x >40
类比归纳
40< x <50
解法探究
【问题3】利用数轴来确定不等式组的解集:
x >3
x >-1
(1)
∴不等式组的解集是: x >3
x < 3
x <-1
(2)
∴不等式组的解集是: x <-1
x < 3
x >-1
(3)
∴不等式组的解集是: -1< x <3
x > 3
x <-1
(4)
3
-1
3
-1
3
-1
3
-1
∴不等式组的解集是: 无解
例题演示
2x-1> x +1 , ①
x+8 <4x-1 ; ②
(1)
2x+3≥ x +11 , ①
-1<2-x . ②
(2)
2x+5
3
【问题4】解下列不等式组:
2
3
例题演示
解:(1)解不等式①得x>2.
解不等式②得x>3.
把不等式① 和②的解集在数轴上表示出来:
从图中可以找到两个不等式解集的公共部分,得不等式组的解集是: x >3.
同学们自己完成第二题.
2x-1> x +1 , ①
x+8 <4x-1 ; ②
(1)
例题演示
x取哪些整数值时,不等式5x+2>3(x-1)
与 x-1≤7 - x 都成立?
分析:要求x的整数解,需先确定x的取值范围(即求出不等式组的解集),解集中的整数就是x可取的整数值.
本节课你有什么收获?
类似于方程组,把这两个不等式合起来,组成一个一元一次不等式组。
归纳解一元一次不等式组的步骤:
1.求出不等式组中各个不等式的解集;
2.利用数轴,求出这些不等式解集的公共部分;
3.写出不等式组的解集。
求不等式组的解集的过程叫做解不等式组
一元一次不等式组中各不等式解集的公共部分叫作一元一次不等式组的解集
1.不等式组
的解集为( )
.
B.
C.
D.无解
A.
学以致用
2.已知不等式①,②,③的解集在数轴上的表示如图所示,则它们的公共部分的解集是( )
A.-1≤x<3 B.1≤x<3 C.-1≤x<1 D.无解
B
B
3、解不等式组
解不等式
得____,
解不等式
得____,
所以不等式组的解集是___ __.
4、不等式组
的正整数解是( )
A.0和1 B.2和3 C.1和3 D.1和2
D
-3<x≤0
x≤0
x>-3
谢谢聆听
