2021-2022学年山东省济宁学院附中九年级(上)期末数学试卷(五四学制)(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年山东省济宁学院附中九年级(上)期末数学试卷(五四学制)(Word版,附答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 15:25:38 | ||
图片预览




文档简介
2021-2022学年山东省济宁学院附中九年级第一学期期末数学试卷(五四学制)
一、选择题(共10小题,共30分)
1.若分式在实数范围内有意义,则x的取值范围是( )
A.x≠﹣5 B.x≠0 C.x≠5 D.x>﹣5
2.若x=+1,则代数式x2﹣2x+2的值为( )
A.7 B.4 C.3 D.3﹣2
3.有一枚质地均匀的正方体骰子,六个面上分别刻有1到6的点数.将它投掷两次,则两次掷得骰子朝上一面的点数之和为5的概率是( )
A. B. C. D.
4.如图,将一个棱长为3的正方体表面涂上颜色,再把它分割成棱长为1的小正方体,将它们全部放入一个不透明盒子中摇匀,随机取出一个小正方体,有三个面被涂色的概率为( )
A. B. C. D.
5.如图,四边形ABCD内接于⊙O,点P为边AD上任意一点(点P不与点A,D重合)连接CP.若∠B=120°,则∠APC的度数可能为( )
A.30° B.45° C.50° D.65°
6.如图,在⊙O中,弦CD与直径AB相交于点E,连接OC,BD.若∠ABD=20°,∠AED=80°,则∠COB的度数为( )
A.80° B.100° C.120° D.140°
7.如图,面积为18的正方形ABCD内接于⊙O,则的长度为( )
A.9π B.π C.π D.π
8.如图,正方形ABCD的边长为4,分别以正方形的三条边为直径在正方形内部作半圆,则阴影部分的面积是( )
A. B.π﹣2 C.2π﹣4 D.4π﹣8
9.已知f(1)=2(取1×2计算结果的末位数字),f(2)=6(取2×3计算结果的末位数字),f(3)=2(取3×4计算结果的末位数字),…,则f(1)+f(2)+f(3)+…+f(2022)的值为( )
A.2020 B.4040 C.4048 D.4042
10.如图,在矩形ABCD中,AB=6,AD=8,点O在对角线BD上,以OB为半径作⊙O交BC于点E,连接DE;若DE是⊙O的切线,此时⊙O的半径为( )
A. B. C. D.
二、填空题(5小题,共15分)
11.计算:= .
12.某鱼塘里养了1600条鲤鱼、若干条草鱼和800条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在0.5左右,若该鱼塘主随机在鱼塘捕捞一条鱼,则捞到鲤鱼的概率约为 .
13.如图,将半径为3cm的圆形纸片剪掉,余下部分围成一个圆锥的侧面,则这个圆锥的高是 cm.
14.在直径为20m的的圆柱型油槽内注入一些油后,截面如图所示,液面宽AB=12m,如果继续向油槽内注油,使液面宽为16m,那么液面上升了 m.
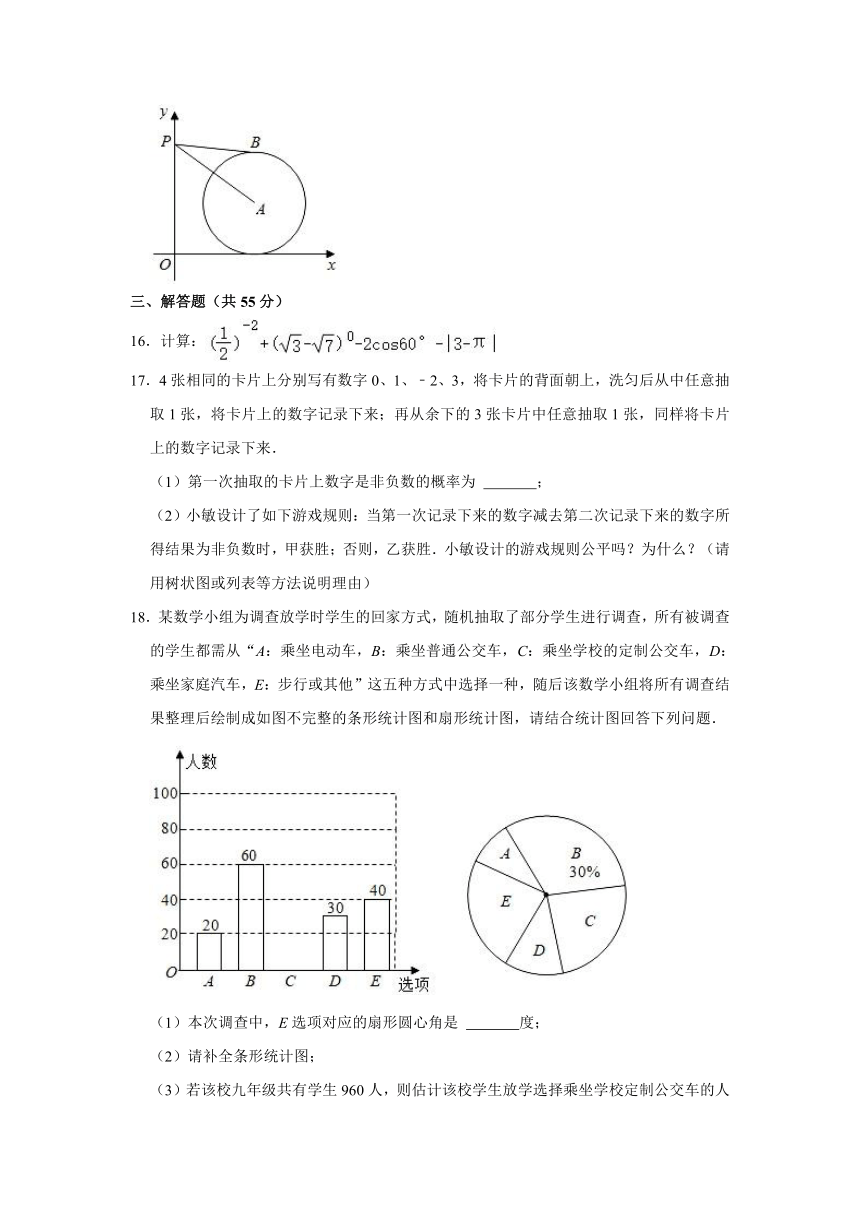
15.如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 .
三、解答题(共55分)
16.计算:
17.4张相同的卡片上分别写有数字0、1、﹣2、3,将卡片的背面朝上,洗匀后从中任意抽取1张,将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.
(1)第一次抽取的卡片上数字是非负数的概率为 ;
(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗?为什么?(请用树状图或列表等方法说明理由)
18.某数学小组为调查放学时学生的回家方式,随机抽取了部分学生进行调查,所有被调查的学生都需从“A:乘坐电动车,B:乘坐普通公交车,C:乘坐学校的定制公交车,D:乘坐家庭汽车,E:步行或其他”这五种方式中选择一种,随后该数学小组将所有调查结果整理后绘制成如图不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
(1)本次调查中,E选项对应的扇形圆心角是 度;
(2)请补全条形统计图;
(3)若该校九年级共有学生960人,则估计该校学生放学选择乘坐学校定制公交车的人数是 ;
(4)若甲、乙两名学生放学时从A、B、C、D、E五种方式中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两名学生恰好选择同一种方式的概率.
19.如图,已知弓形的弦长AB=12,弓高CD=2,(CD⊥AB,并经过圆心O).
(1)请利用尺规作图的方法找到圆心O;
(2)求弓形所在⊙O的半径的长.
20.如图,AB为⊙O的直径,半径OD⊥AB于O,⊙O的弦CD与AB相交于点F,⊙O的切线CE交AB的延长线于点E.
(1)求证:EC=EF;
(2)若⊙O的半径长为3,且BF=BE,求DF的长.
21.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,过D作直线DG∥BC.
(1)若∠ACB=80°,则∠ADB= ;∠AEB= .
(2)求证:DE=CD;
(3)求证:DG是⊙O的切线.
22.如图1,在平面直角坐标系中,点A,B的坐标分别为A(8,0)和B(0,6),点P为x轴负半轴上的一个动点,画△ABP的外接圆,圆心为M,连接BM并延长交圆于点C,连接CP.
(1)求证:∠OBP=∠ABC.
(2)当⊙M的直径为14时,求点P的坐标.
(3)如图2,连接OC,求OC的最小值和OC达到最小值时△ABP的外接圆圆心M的坐标.
参考答案
一、选择题(共10小题,共30分)
1.若分式在实数范围内有意义,则x的取值范围是( )
A.x≠﹣5 B.x≠0 C.x≠5 D.x>﹣5
【分析】根据分式成立的条件列不等式求解.
解:根据分式成立的条件,可得:x+5≠0,
∴x≠﹣5,
故选:A.
2.若x=+1,则代数式x2﹣2x+2的值为( )
A.7 B.4 C.3 D.3﹣2
【分析】利用条件得到x﹣1=,两边平方得x2﹣2x=1,然后利用整体代入的方法计算.
解:∵x=+1,
∴x﹣1=,
∴(x﹣1)2=2,即x2﹣2x+1=2,
∴x2﹣2x=1,
∴x2﹣2x+2=1+2=3.
故选:C.
3.有一枚质地均匀的正方体骰子,六个面上分别刻有1到6的点数.将它投掷两次,则两次掷得骰子朝上一面的点数之和为5的概率是( )
A. B. C. D.
【分析】列表可知共有36种等可能的情况,两次掷得骰子朝上一面的点数之和为5的情况有4种,再由概率公式求解即可.
解:列表如下:
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
由表可知共有36种等可能的情况,两次掷得骰子朝上一面的点数之和为5的情况有4种,
∴两次掷得骰子朝上一面的点数之和为5的概率为=,
故选:A.
4.如图,将一个棱长为3的正方体表面涂上颜色,再把它分割成棱长为1的小正方体,将它们全部放入一个不透明盒子中摇匀,随机取出一个小正方体,有三个面被涂色的概率为( )
A. B. C. D.
【分析】直接根据题意得出恰有三个面被涂色的有8个,再利用概率公式求出答案.
解:由题意可得:小立方体一共有27个,恰有三个面被涂色.的有8个,
故取得的小正方体恰有三个面被涂色.的概率为.
故选:B.
5.如图,四边形ABCD内接于⊙O,点P为边AD上任意一点(点P不与点A,D重合)连接CP.若∠B=120°,则∠APC的度数可能为( )
A.30° B.45° C.50° D.65°
【分析】由圆内接四边形的性质得∠D度数为60°,再由∠APC为△PCD的外角求解.
解:∵四边形ABCD内接于⊙O,
∴∠B+∠D=180°,
∵∠B=120°,
∴∠D=180°﹣∠B=60°,
∵∠APC为△PCD的外角,
∴∠APC>∠D,只有D满足题意.
故选:D.
6.如图,在⊙O中,弦CD与直径AB相交于点E,连接OC,BD.若∠ABD=20°,∠AED=80°,则∠COB的度数为( )
A.80° B.100° C.120° D.140°
【分析】根据三角形的外角性质求出∠D,根据圆周角定理得出∠D=COB,求出∠COB=2∠D,再代入求出答案即可.
解:∵∠ABD=20°,∠AED=80°,
∴∠D=∠AED﹣∠ABD=80°﹣20°=60°,
∴∠COB=2∠D=120°,
故选:C.
7.如图,面积为18的正方形ABCD内接于⊙O,则的长度为( )
A.9π B.π C.π D.π
【分析】连接OA、OB,则△OAB为等腰直角三角形,由正方形面积为18,可求边长为3,进而可得半径为3,根据弧长公式可求弧AB的长.
解:如图
连接OA,OB,则OA=OB,
∵四边形ABCD是正方形,
∴∠AOB=90°,
∴△OAB是等腰直角三角形,
∵正方形ABCD的面积是18,
∴AB==3,
∴OA=OB=3,
∴弧AB的长L===,
故选:C.
8.如图,正方形ABCD的边长为4,分别以正方形的三条边为直径在正方形内部作半圆,则阴影部分的面积是( )
A. B.π﹣2 C.2π﹣4 D.4π﹣8
【分析】如图,设三个半圆交于O,连接OA、OD,得到△AOD是等腰直角三角形,根据扇形和三角形的面积公式即可得到结论.
解:如图,设三个半圆交于O,
连接OA、OD,
则△AOD是等腰直角三角形,
∵正方形ABCD的边长为4,
∴半圆的半径为2,
则S半圆O= π×22=2π,S△AOD=×4×2=4,
∴图中阴影部分的面积=2(S半圆O﹣S△AOD)
=2(2π﹣4)=4π﹣8,
故选:D.
9.已知f(1)=2(取1×2计算结果的末位数字),f(2)=6(取2×3计算结果的末位数字),f(3)=2(取3×4计算结果的末位数字),…,则f(1)+f(2)+f(3)+…+f(2022)的值为( )
A.2020 B.4040 C.4048 D.4042
【分析】通过计算发现,运算结果每5次循环一次,并且f(1)+f(2)+f(3)+f(4)+f(5)=10,再由2022÷5=404…2,即可求解.
解:∵f(1)=2,f(2)=6,f(3)=2,
∴f(4)=0,f(5)=0,f(6)=2,f(7)=6,f(8)=2,f(9)=0,f(10)=0,…,
∴运算结果每5次循环一次,
∵f(1)+f(2)+f(3)+f(4)+f(5)=10,
∴f(1)+f(2)+f(3)+…+f(2022)=10×404+8=4048,
故选:C.
10.如图,在矩形ABCD中,AB=6,AD=8,点O在对角线BD上,以OB为半径作⊙O交BC于点E,连接DE;若DE是⊙O的切线,此时⊙O的半径为( )
A. B. C. D.
【分析】根据矩形的性质和勾股定理可得BD,根据切线的性质∠DEO=90°,根据同角的余角相等得∠OEB=∠EDC,则∠DBC=∠EDC,根据cos∠DBC==,可得cos∠EDC==,可求得DE=,在Rt△ODE中,利用勾股定理即可得⊙O的半径OE的值.
解:∵四边形ABCD是矩形,
∴∠A=∠C=90°,BC=AD=8,DC=AB=6,
在Rt△ADB中,∠C=90°,
∴BD==10,
∵DE是⊙O的切线,
∴OE⊥DE,
∴∠OEB+∠DEC=90°,
∵∠DEC+∠EDC=90°,
∴∠OEB=∠EDC,
∵OB=OE,
∴∠OEB=∠DBC,
∴cos∠EDC==cos∠DBC==,
∴DE=,
设OB=OE=r,
在Rt△ODE中,OD2=OE2+DE2,
∴(10﹣r)2=r2+()2,
解得r=.
故选:D.
二、填空题(5小题,共15分)
11.计算:= 5 .
【分析】根据二次根式的基本性质进行解答即可.
解:原式==5.
故答案为:5.
12.某鱼塘里养了1600条鲤鱼、若干条草鱼和800条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在0.5左右,若该鱼塘主随机在鱼塘捕捞一条鱼,则捞到鲤鱼的概率约为 .
【分析】根据捕捞到草鱼的频率可以估计出放入鱼塘中鱼的总数量,从而可以得到捞到鲤鱼的概率.
解:∵捕捞到草鱼的频率稳定在0.5左右,
设草鱼的条数为x,可得:;
解得:x=2400,
∴由题意可得,捞到鲤鱼的概率为,
故答案为:
13.如图,将半径为3cm的圆形纸片剪掉,余下部分围成一个圆锥的侧面,则这个圆锥的高是 cm.
【分析】根据圆锥的底面周长等于侧面展开图的弧长可以计算圆锥的底面半径,利用勾股定理即可求得圆锥的高.
解:∵将半径为3cm的圆形纸片剪掉三分之一,余下部分围成一个圆锥的侧面,
∴围成圆锥的弧长所对圆心角度数是×360°=240°,
设这个圆锥的底面半径为rcm,
则2πr=,
∴r=2,
∴圆锥的高为=(cm).
故答案为:.
14.在直径为20m的的圆柱型油槽内注入一些油后,截面如图所示,液面宽AB=12m,如果继续向油槽内注油,使液面宽为16m,那么液面上升了 2或14 m.
【分析】根据垂径定理、勾股定理求弦心距,再作和或差分别求解即可.
解:设圆柱型油槽的圆心为O,
分两种情况:
①AB、GH在圆心O的同侧时,连接OA、OG,过O作OC⊥AB于C,
设GH交OD于E,
依题意得:OA=OG=10(m),AB∥GH,AB=12m,GH=16m,
则OC⊥GH,
由垂径定理,得AC=AB=6(m),EG=GH=8(m),
在Rt△OAC中,由勾股定理得:OC===8(m),
在Rt△OEG中,由勾股定理得:OE===6(m),
∴CE=OC﹣OE=2(m);
②AB、G'H'在圆心O的异侧时,连接OG',过O作OE'⊥G'H'于E',
同①得:OE'=6(m),
∴CE'=OC+OE'=14(m);
综上所述,液面上升了2m或14m,
故答案为:2或14.
15.如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 (0,11) .
【分析】连接AB,过点A分别作AC⊥x轴、AD⊥y轴,利用根据圆的切线性质可知△PAB、△AOC为直角三角形,AB=AC=5,利用直角三角形中30°角的性质和勾股定理分别求出AP、AD的长度,进而求出OD、PD的长度即可求得答案.
解:过点A分别作AC⊥x轴于点C、AD⊥y轴于点D,连接AB,
当点P在点D是上方时,如图,
∵AD⊥y轴,AC⊥x轴,
∴四边形ADOC为矩形,
∴AC=OD,OC=AD,
∵⊙A与x轴相切,
∴AC为⊙A的半径,
∵点A坐标为(8,5),
∴AC=OD=5,OC=AD=8,
∵PB是切线,
∴AB⊥PB,
∵∠APB=30°,
∴PA=2AB=10,
在Rt△PAD中,根据勾股定理得,
PD===6,
∴OP=PD+DO=11,
∵点P在y轴的正半轴上,
∴点P坐标为(0,11),
故答案为:(0,11).
三、解答题(共55分)
16.计算:
【分析】分别计算负整数指数幂、零指数幂,代入cos60°=,进行运算,然后合并即可得出答案.
解:原式=4+1﹣1﹣π+3=7﹣π.
17.4张相同的卡片上分别写有数字0、1、﹣2、3,将卡片的背面朝上,洗匀后从中任意抽取1张,将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.
(1)第一次抽取的卡片上数字是非负数的概率为 ;
(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗?为什么?(请用树状图或列表等方法说明理由)
【分析】(1)利用概率公式求解即可;
(2)利用列表法列举出所有可能结果,再利用概率公式得出甲、乙获胜的概率,即可得出答案.
解:(1)第一次抽取的卡片上数字是非负数的概率为,
故答案为:;
(2)小敏设计的游戏规则公平,理由如下:
列表如下:
0 1 ﹣2 3
0 1 ﹣2 3
1 ﹣1 ﹣3 2
﹣2 2 3 5
3 ﹣3 ﹣2 ﹣5
由表可知,共有12种等可能结果,其中结果为非负数的有6种结果,结果为负数的有6种结果,
∴甲获胜的概率=乙获胜的概率==,
∴小敏设计的游戏规则公平.
18.某数学小组为调查放学时学生的回家方式,随机抽取了部分学生进行调查,所有被调查的学生都需从“A:乘坐电动车,B:乘坐普通公交车,C:乘坐学校的定制公交车,D:乘坐家庭汽车,E:步行或其他”这五种方式中选择一种,随后该数学小组将所有调查结果整理后绘制成如图不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
(1)本次调查中,E选项对应的扇形圆心角是 72 度;
(2)请补全条形统计图;
(3)若该校九年级共有学生960人,则估计该校学生放学选择乘坐学校定制公交车的人数是 240人 ;
(4)若甲、乙两名学生放学时从A、B、C、D、E五种方式中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两名学生恰好选择同一种方式的概率.
【分析】(1)由B的人数和所占百分比求出本次调查的学生人数,即可解决问题;
(2)求出C选项的人数,补全条形统计图即可;
(3)由该校九年级共有学生人数乘以选择乘坐学校定制公交车的人数所占的比例即可;
(4)画树状图,共有25种等可能的结果,其中甲、乙两名学生恰好选择同一种方式的结果有5种,再由概率公式求解即可.
解:(1)本次调查的学生人数为:60÷30%=200(人),
则E选项对应的扇形圆心角是360°×=72°,
故答案为:72;
(2)C选项的人数为:200﹣20﹣60﹣30﹣40=50(人),
补全条形统计图如下:
(3)960×=240(人),
即估计该校学生放学选择乘坐学校定制公交车的人数是240人;
(4)画树状图如下:
共有25种等可能的结果,其中甲、乙两名学生恰好选择同一种方式的结果有5种,
∴甲、乙两名学生恰好选择同一种方式的概率为=.
19.如图,已知弓形的弦长AB=12,弓高CD=2,(CD⊥AB,并经过圆心O).
(1)请利用尺规作图的方法找到圆心O;
(2)求弓形所在⊙O的半径的长.
【分析】(1)作线段AC的垂直平分线交CD的延长线于点O,点O即为所求;
(2)连接AO,设OA=x,利用勾股定理求解即可.
解:(1)如图,点O即为所求;
(2)连接AO,设OA=x,
∵OC⊥AB,
∴AD=DB=6,
在Rt△ADO中,∵OA2=AD2+OD2,
∴x2=62+(x﹣2)2,
解得x=10,
∴OA=10,即⊙O的半径为10.
20.如图,AB为⊙O的直径,半径OD⊥AB于O,⊙O的弦CD与AB相交于点F,⊙O的切线CE交AB的延长线于点E.
(1)求证:EC=EF;
(2)若⊙O的半径长为3,且BF=BE,求DF的长.
【分析】(1)连接OC,根据CE与⊙O相切、半径OD⊥AB以及OC=OD,即可证得∠ECF=∠EFC,从而证得EC=EF;
(2)设BF=BE=x,根据勾股定理得OC2+CE2=OE2,求出x,即可求得DF的长.
【解答】(1)证明:如图,连接OC.
∵CE切⊙O于点C,
∴OC⊥CE,即∠OCF+∠ECF=90°,
∵OD⊥AB,
∴∠D+∠DFO=90°,
∵OC=OD,
∴∠D=∠OCD,
∴∠ECF=∠OFD,
又∵∠OFD=∠EFC
∴∠ECF=∠EFC,
∴EC=EF;
(2)解:如图,∵BF=BE,
设BF=BE=x,则EC=EF=2x,OE=3+x,
在Rt△OCE中,OC2+CE2=OE2,
∴32+(2x)2=(3+x)2,
解得x1=0(舍),x2=2,
∴OF=OB﹣FB=1,
在Rt△ODF中,DF===.
21.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,过D作直线DG∥BC.
(1)若∠ACB=80°,则∠ADB= 80° ;∠AEB= 130° .
(2)求证:DE=CD;
(3)求证:DG是⊙O的切线.
【分析】(1)由圆周角定理可得∠ACB=∠ADB=70°,由三角形的内心的性质可得∠AEB=125°;
(2)由三角形的内心的性质可得AE平分∠BAC,BE平分∠ABC,可得∠BAE=∠CAE,∠ABE=∠CBE,由外角的性质可得∠BED=∠DBE,可证DE=CD;
(3)由垂径定理可得OD⊥BC,由平行线的性质可得OD⊥DG,可得结论.
【解答】(1)解:如图,连接OD,
∵=,
∴∠ACB=∠ADB=80°,
∴∠ABC+∠BAC=100°,
∵点E是△ABC的内心,
∴AE平分∠BAC,BE平分∠ABC,
∴∠BAE=∠CAE,∠ABE=∠CBE,
∴∠BAE+∠ABE=50°,
∴∠AEB=130°,
故答案为:80°,130°;
(2)证明:∵∠BAE=∠CAE,
∴=,
∴BD=CD,
∵∠BAE=∠CAE=∠CBD,∠ABE=∠CBE,
∴∠BED=∠BAE+∠ABE=∠CBD+∠CBE=∠DBE,
∴BD=DE,
∴DE=CD;
(3)证明:∵=,
∴OD⊥BC,
∵DG∥BC,
∴OD⊥DG,
又∵OD是半径,
∴DG是⊙O的切线.
22.如图1,在平面直角坐标系中,点A,B的坐标分别为A(8,0)和B(0,6),点P为x轴负半轴上的一个动点,画△ABP的外接圆,圆心为M,连接BM并延长交圆于点C,连接CP.
(1)求证:∠OBP=∠ABC.
(2)当⊙M的直径为14时,求点P的坐标.
(3)如图2,连接OC,求OC的最小值和OC达到最小值时△ABP的外接圆圆心M的坐标.
【分析】(1)如图1,连接AC,由圆周角定理得到:∠BAC=∠BOP=90°,∠ACB=∠APB,所以等角的余角相等:∠OBP=∠ABC.
(2)根据勾股定理求得AB=10,AC=4;由“两角法”证得△OBP∽△ABC,则该相似三角形的对应边成比例(),由此求得线段OP的长度,结合平面直角坐标系得到点P的坐标为;
(3)如图2,记直线AC与y轴的交点为E,由题意知∠OAE=∠OBA=90°﹣∠BAO,当OC最小时,OC⊥AE,此时,通过解直角三角形求得线段OC的长度;易得点C的坐标为根据中点坐标的求法得到点M的坐标即可.
解:(1)如图1,连接AC,
∵BC为⊙M的直径,
∴∠BAC=∠BOP=90°,
∵∠ACB=∠APB,
∴∠OBP+∠APB=∠ABC+∠ACB=90°,
∴∠OBP=∠ABC.
(2)∵∠BAC=90°,A(8,0),B(6,0)
∴OB=6,OA=8,
∴AB=10
∴=
∵∠BOP=∠BAC,∠OBP=∠ABC,
∴△OBP∽△ABC,
∴,
∴=,
∴点P的坐标为;
(3)如图2,记直线AC与y轴的交点为E,
∵AC⊥AB,则∠OAE=∠OBA=90°﹣∠BAO,
当OC最小时,OC⊥AE,
此时,OC=OA sin∠OAE=OA sin∠OBA=.
求得点C的坐标为.
又∵点M为BC的中点
∴,,
∴点M的坐标为.
一、选择题(共10小题,共30分)
1.若分式在实数范围内有意义,则x的取值范围是( )
A.x≠﹣5 B.x≠0 C.x≠5 D.x>﹣5
2.若x=+1,则代数式x2﹣2x+2的值为( )
A.7 B.4 C.3 D.3﹣2
3.有一枚质地均匀的正方体骰子,六个面上分别刻有1到6的点数.将它投掷两次,则两次掷得骰子朝上一面的点数之和为5的概率是( )
A. B. C. D.
4.如图,将一个棱长为3的正方体表面涂上颜色,再把它分割成棱长为1的小正方体,将它们全部放入一个不透明盒子中摇匀,随机取出一个小正方体,有三个面被涂色的概率为( )
A. B. C. D.
5.如图,四边形ABCD内接于⊙O,点P为边AD上任意一点(点P不与点A,D重合)连接CP.若∠B=120°,则∠APC的度数可能为( )
A.30° B.45° C.50° D.65°
6.如图,在⊙O中,弦CD与直径AB相交于点E,连接OC,BD.若∠ABD=20°,∠AED=80°,则∠COB的度数为( )
A.80° B.100° C.120° D.140°
7.如图,面积为18的正方形ABCD内接于⊙O,则的长度为( )
A.9π B.π C.π D.π
8.如图,正方形ABCD的边长为4,分别以正方形的三条边为直径在正方形内部作半圆,则阴影部分的面积是( )
A. B.π﹣2 C.2π﹣4 D.4π﹣8
9.已知f(1)=2(取1×2计算结果的末位数字),f(2)=6(取2×3计算结果的末位数字),f(3)=2(取3×4计算结果的末位数字),…,则f(1)+f(2)+f(3)+…+f(2022)的值为( )
A.2020 B.4040 C.4048 D.4042
10.如图,在矩形ABCD中,AB=6,AD=8,点O在对角线BD上,以OB为半径作⊙O交BC于点E,连接DE;若DE是⊙O的切线,此时⊙O的半径为( )
A. B. C. D.
二、填空题(5小题,共15分)
11.计算:= .
12.某鱼塘里养了1600条鲤鱼、若干条草鱼和800条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在0.5左右,若该鱼塘主随机在鱼塘捕捞一条鱼,则捞到鲤鱼的概率约为 .
13.如图,将半径为3cm的圆形纸片剪掉,余下部分围成一个圆锥的侧面,则这个圆锥的高是 cm.
14.在直径为20m的的圆柱型油槽内注入一些油后,截面如图所示,液面宽AB=12m,如果继续向油槽内注油,使液面宽为16m,那么液面上升了 m.
15.如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 .
三、解答题(共55分)
16.计算:
17.4张相同的卡片上分别写有数字0、1、﹣2、3,将卡片的背面朝上,洗匀后从中任意抽取1张,将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.
(1)第一次抽取的卡片上数字是非负数的概率为 ;
(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗?为什么?(请用树状图或列表等方法说明理由)
18.某数学小组为调查放学时学生的回家方式,随机抽取了部分学生进行调查,所有被调查的学生都需从“A:乘坐电动车,B:乘坐普通公交车,C:乘坐学校的定制公交车,D:乘坐家庭汽车,E:步行或其他”这五种方式中选择一种,随后该数学小组将所有调查结果整理后绘制成如图不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
(1)本次调查中,E选项对应的扇形圆心角是 度;
(2)请补全条形统计图;
(3)若该校九年级共有学生960人,则估计该校学生放学选择乘坐学校定制公交车的人数是 ;
(4)若甲、乙两名学生放学时从A、B、C、D、E五种方式中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两名学生恰好选择同一种方式的概率.
19.如图,已知弓形的弦长AB=12,弓高CD=2,(CD⊥AB,并经过圆心O).
(1)请利用尺规作图的方法找到圆心O;
(2)求弓形所在⊙O的半径的长.
20.如图,AB为⊙O的直径,半径OD⊥AB于O,⊙O的弦CD与AB相交于点F,⊙O的切线CE交AB的延长线于点E.
(1)求证:EC=EF;
(2)若⊙O的半径长为3,且BF=BE,求DF的长.
21.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,过D作直线DG∥BC.
(1)若∠ACB=80°,则∠ADB= ;∠AEB= .
(2)求证:DE=CD;
(3)求证:DG是⊙O的切线.
22.如图1,在平面直角坐标系中,点A,B的坐标分别为A(8,0)和B(0,6),点P为x轴负半轴上的一个动点,画△ABP的外接圆,圆心为M,连接BM并延长交圆于点C,连接CP.
(1)求证:∠OBP=∠ABC.
(2)当⊙M的直径为14时,求点P的坐标.
(3)如图2,连接OC,求OC的最小值和OC达到最小值时△ABP的外接圆圆心M的坐标.
参考答案
一、选择题(共10小题,共30分)
1.若分式在实数范围内有意义,则x的取值范围是( )
A.x≠﹣5 B.x≠0 C.x≠5 D.x>﹣5
【分析】根据分式成立的条件列不等式求解.
解:根据分式成立的条件,可得:x+5≠0,
∴x≠﹣5,
故选:A.
2.若x=+1,则代数式x2﹣2x+2的值为( )
A.7 B.4 C.3 D.3﹣2
【分析】利用条件得到x﹣1=,两边平方得x2﹣2x=1,然后利用整体代入的方法计算.
解:∵x=+1,
∴x﹣1=,
∴(x﹣1)2=2,即x2﹣2x+1=2,
∴x2﹣2x=1,
∴x2﹣2x+2=1+2=3.
故选:C.
3.有一枚质地均匀的正方体骰子,六个面上分别刻有1到6的点数.将它投掷两次,则两次掷得骰子朝上一面的点数之和为5的概率是( )
A. B. C. D.
【分析】列表可知共有36种等可能的情况,两次掷得骰子朝上一面的点数之和为5的情况有4种,再由概率公式求解即可.
解:列表如下:
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
由表可知共有36种等可能的情况,两次掷得骰子朝上一面的点数之和为5的情况有4种,
∴两次掷得骰子朝上一面的点数之和为5的概率为=,
故选:A.
4.如图,将一个棱长为3的正方体表面涂上颜色,再把它分割成棱长为1的小正方体,将它们全部放入一个不透明盒子中摇匀,随机取出一个小正方体,有三个面被涂色的概率为( )
A. B. C. D.
【分析】直接根据题意得出恰有三个面被涂色的有8个,再利用概率公式求出答案.
解:由题意可得:小立方体一共有27个,恰有三个面被涂色.的有8个,
故取得的小正方体恰有三个面被涂色.的概率为.
故选:B.
5.如图,四边形ABCD内接于⊙O,点P为边AD上任意一点(点P不与点A,D重合)连接CP.若∠B=120°,则∠APC的度数可能为( )
A.30° B.45° C.50° D.65°
【分析】由圆内接四边形的性质得∠D度数为60°,再由∠APC为△PCD的外角求解.
解:∵四边形ABCD内接于⊙O,
∴∠B+∠D=180°,
∵∠B=120°,
∴∠D=180°﹣∠B=60°,
∵∠APC为△PCD的外角,
∴∠APC>∠D,只有D满足题意.
故选:D.
6.如图,在⊙O中,弦CD与直径AB相交于点E,连接OC,BD.若∠ABD=20°,∠AED=80°,则∠COB的度数为( )
A.80° B.100° C.120° D.140°
【分析】根据三角形的外角性质求出∠D,根据圆周角定理得出∠D=COB,求出∠COB=2∠D,再代入求出答案即可.
解:∵∠ABD=20°,∠AED=80°,
∴∠D=∠AED﹣∠ABD=80°﹣20°=60°,
∴∠COB=2∠D=120°,
故选:C.
7.如图,面积为18的正方形ABCD内接于⊙O,则的长度为( )
A.9π B.π C.π D.π
【分析】连接OA、OB,则△OAB为等腰直角三角形,由正方形面积为18,可求边长为3,进而可得半径为3,根据弧长公式可求弧AB的长.
解:如图
连接OA,OB,则OA=OB,
∵四边形ABCD是正方形,
∴∠AOB=90°,
∴△OAB是等腰直角三角形,
∵正方形ABCD的面积是18,
∴AB==3,
∴OA=OB=3,
∴弧AB的长L===,
故选:C.
8.如图,正方形ABCD的边长为4,分别以正方形的三条边为直径在正方形内部作半圆,则阴影部分的面积是( )
A. B.π﹣2 C.2π﹣4 D.4π﹣8
【分析】如图,设三个半圆交于O,连接OA、OD,得到△AOD是等腰直角三角形,根据扇形和三角形的面积公式即可得到结论.
解:如图,设三个半圆交于O,
连接OA、OD,
则△AOD是等腰直角三角形,
∵正方形ABCD的边长为4,
∴半圆的半径为2,
则S半圆O= π×22=2π,S△AOD=×4×2=4,
∴图中阴影部分的面积=2(S半圆O﹣S△AOD)
=2(2π﹣4)=4π﹣8,
故选:D.
9.已知f(1)=2(取1×2计算结果的末位数字),f(2)=6(取2×3计算结果的末位数字),f(3)=2(取3×4计算结果的末位数字),…,则f(1)+f(2)+f(3)+…+f(2022)的值为( )
A.2020 B.4040 C.4048 D.4042
【分析】通过计算发现,运算结果每5次循环一次,并且f(1)+f(2)+f(3)+f(4)+f(5)=10,再由2022÷5=404…2,即可求解.
解:∵f(1)=2,f(2)=6,f(3)=2,
∴f(4)=0,f(5)=0,f(6)=2,f(7)=6,f(8)=2,f(9)=0,f(10)=0,…,
∴运算结果每5次循环一次,
∵f(1)+f(2)+f(3)+f(4)+f(5)=10,
∴f(1)+f(2)+f(3)+…+f(2022)=10×404+8=4048,
故选:C.
10.如图,在矩形ABCD中,AB=6,AD=8,点O在对角线BD上,以OB为半径作⊙O交BC于点E,连接DE;若DE是⊙O的切线,此时⊙O的半径为( )
A. B. C. D.
【分析】根据矩形的性质和勾股定理可得BD,根据切线的性质∠DEO=90°,根据同角的余角相等得∠OEB=∠EDC,则∠DBC=∠EDC,根据cos∠DBC==,可得cos∠EDC==,可求得DE=,在Rt△ODE中,利用勾股定理即可得⊙O的半径OE的值.
解:∵四边形ABCD是矩形,
∴∠A=∠C=90°,BC=AD=8,DC=AB=6,
在Rt△ADB中,∠C=90°,
∴BD==10,
∵DE是⊙O的切线,
∴OE⊥DE,
∴∠OEB+∠DEC=90°,
∵∠DEC+∠EDC=90°,
∴∠OEB=∠EDC,
∵OB=OE,
∴∠OEB=∠DBC,
∴cos∠EDC==cos∠DBC==,
∴DE=,
设OB=OE=r,
在Rt△ODE中,OD2=OE2+DE2,
∴(10﹣r)2=r2+()2,
解得r=.
故选:D.
二、填空题(5小题,共15分)
11.计算:= 5 .
【分析】根据二次根式的基本性质进行解答即可.
解:原式==5.
故答案为:5.
12.某鱼塘里养了1600条鲤鱼、若干条草鱼和800条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在0.5左右,若该鱼塘主随机在鱼塘捕捞一条鱼,则捞到鲤鱼的概率约为 .
【分析】根据捕捞到草鱼的频率可以估计出放入鱼塘中鱼的总数量,从而可以得到捞到鲤鱼的概率.
解:∵捕捞到草鱼的频率稳定在0.5左右,
设草鱼的条数为x,可得:;
解得:x=2400,
∴由题意可得,捞到鲤鱼的概率为,
故答案为:
13.如图,将半径为3cm的圆形纸片剪掉,余下部分围成一个圆锥的侧面,则这个圆锥的高是 cm.
【分析】根据圆锥的底面周长等于侧面展开图的弧长可以计算圆锥的底面半径,利用勾股定理即可求得圆锥的高.
解:∵将半径为3cm的圆形纸片剪掉三分之一,余下部分围成一个圆锥的侧面,
∴围成圆锥的弧长所对圆心角度数是×360°=240°,
设这个圆锥的底面半径为rcm,
则2πr=,
∴r=2,
∴圆锥的高为=(cm).
故答案为:.
14.在直径为20m的的圆柱型油槽内注入一些油后,截面如图所示,液面宽AB=12m,如果继续向油槽内注油,使液面宽为16m,那么液面上升了 2或14 m.
【分析】根据垂径定理、勾股定理求弦心距,再作和或差分别求解即可.
解:设圆柱型油槽的圆心为O,
分两种情况:
①AB、GH在圆心O的同侧时,连接OA、OG,过O作OC⊥AB于C,
设GH交OD于E,
依题意得:OA=OG=10(m),AB∥GH,AB=12m,GH=16m,
则OC⊥GH,
由垂径定理,得AC=AB=6(m),EG=GH=8(m),
在Rt△OAC中,由勾股定理得:OC===8(m),
在Rt△OEG中,由勾股定理得:OE===6(m),
∴CE=OC﹣OE=2(m);
②AB、G'H'在圆心O的异侧时,连接OG',过O作OE'⊥G'H'于E',
同①得:OE'=6(m),
∴CE'=OC+OE'=14(m);
综上所述,液面上升了2m或14m,
故答案为:2或14.
15.如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 (0,11) .
【分析】连接AB,过点A分别作AC⊥x轴、AD⊥y轴,利用根据圆的切线性质可知△PAB、△AOC为直角三角形,AB=AC=5,利用直角三角形中30°角的性质和勾股定理分别求出AP、AD的长度,进而求出OD、PD的长度即可求得答案.
解:过点A分别作AC⊥x轴于点C、AD⊥y轴于点D,连接AB,
当点P在点D是上方时,如图,
∵AD⊥y轴,AC⊥x轴,
∴四边形ADOC为矩形,
∴AC=OD,OC=AD,
∵⊙A与x轴相切,
∴AC为⊙A的半径,
∵点A坐标为(8,5),
∴AC=OD=5,OC=AD=8,
∵PB是切线,
∴AB⊥PB,
∵∠APB=30°,
∴PA=2AB=10,
在Rt△PAD中,根据勾股定理得,
PD===6,
∴OP=PD+DO=11,
∵点P在y轴的正半轴上,
∴点P坐标为(0,11),
故答案为:(0,11).
三、解答题(共55分)
16.计算:
【分析】分别计算负整数指数幂、零指数幂,代入cos60°=,进行运算,然后合并即可得出答案.
解:原式=4+1﹣1﹣π+3=7﹣π.
17.4张相同的卡片上分别写有数字0、1、﹣2、3,将卡片的背面朝上,洗匀后从中任意抽取1张,将卡片上的数字记录下来;再从余下的3张卡片中任意抽取1张,同样将卡片上的数字记录下来.
(1)第一次抽取的卡片上数字是非负数的概率为 ;
(2)小敏设计了如下游戏规则:当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时,甲获胜;否则,乙获胜.小敏设计的游戏规则公平吗?为什么?(请用树状图或列表等方法说明理由)
【分析】(1)利用概率公式求解即可;
(2)利用列表法列举出所有可能结果,再利用概率公式得出甲、乙获胜的概率,即可得出答案.
解:(1)第一次抽取的卡片上数字是非负数的概率为,
故答案为:;
(2)小敏设计的游戏规则公平,理由如下:
列表如下:
0 1 ﹣2 3
0 1 ﹣2 3
1 ﹣1 ﹣3 2
﹣2 2 3 5
3 ﹣3 ﹣2 ﹣5
由表可知,共有12种等可能结果,其中结果为非负数的有6种结果,结果为负数的有6种结果,
∴甲获胜的概率=乙获胜的概率==,
∴小敏设计的游戏规则公平.
18.某数学小组为调查放学时学生的回家方式,随机抽取了部分学生进行调查,所有被调查的学生都需从“A:乘坐电动车,B:乘坐普通公交车,C:乘坐学校的定制公交车,D:乘坐家庭汽车,E:步行或其他”这五种方式中选择一种,随后该数学小组将所有调查结果整理后绘制成如图不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
(1)本次调查中,E选项对应的扇形圆心角是 72 度;
(2)请补全条形统计图;
(3)若该校九年级共有学生960人,则估计该校学生放学选择乘坐学校定制公交车的人数是 240人 ;
(4)若甲、乙两名学生放学时从A、B、C、D、E五种方式中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两名学生恰好选择同一种方式的概率.
【分析】(1)由B的人数和所占百分比求出本次调查的学生人数,即可解决问题;
(2)求出C选项的人数,补全条形统计图即可;
(3)由该校九年级共有学生人数乘以选择乘坐学校定制公交车的人数所占的比例即可;
(4)画树状图,共有25种等可能的结果,其中甲、乙两名学生恰好选择同一种方式的结果有5种,再由概率公式求解即可.
解:(1)本次调查的学生人数为:60÷30%=200(人),
则E选项对应的扇形圆心角是360°×=72°,
故答案为:72;
(2)C选项的人数为:200﹣20﹣60﹣30﹣40=50(人),
补全条形统计图如下:
(3)960×=240(人),
即估计该校学生放学选择乘坐学校定制公交车的人数是240人;
(4)画树状图如下:
共有25种等可能的结果,其中甲、乙两名学生恰好选择同一种方式的结果有5种,
∴甲、乙两名学生恰好选择同一种方式的概率为=.
19.如图,已知弓形的弦长AB=12,弓高CD=2,(CD⊥AB,并经过圆心O).
(1)请利用尺规作图的方法找到圆心O;
(2)求弓形所在⊙O的半径的长.
【分析】(1)作线段AC的垂直平分线交CD的延长线于点O,点O即为所求;
(2)连接AO,设OA=x,利用勾股定理求解即可.
解:(1)如图,点O即为所求;
(2)连接AO,设OA=x,
∵OC⊥AB,
∴AD=DB=6,
在Rt△ADO中,∵OA2=AD2+OD2,
∴x2=62+(x﹣2)2,
解得x=10,
∴OA=10,即⊙O的半径为10.
20.如图,AB为⊙O的直径,半径OD⊥AB于O,⊙O的弦CD与AB相交于点F,⊙O的切线CE交AB的延长线于点E.
(1)求证:EC=EF;
(2)若⊙O的半径长为3,且BF=BE,求DF的长.
【分析】(1)连接OC,根据CE与⊙O相切、半径OD⊥AB以及OC=OD,即可证得∠ECF=∠EFC,从而证得EC=EF;
(2)设BF=BE=x,根据勾股定理得OC2+CE2=OE2,求出x,即可求得DF的长.
【解答】(1)证明:如图,连接OC.
∵CE切⊙O于点C,
∴OC⊥CE,即∠OCF+∠ECF=90°,
∵OD⊥AB,
∴∠D+∠DFO=90°,
∵OC=OD,
∴∠D=∠OCD,
∴∠ECF=∠OFD,
又∵∠OFD=∠EFC
∴∠ECF=∠EFC,
∴EC=EF;
(2)解:如图,∵BF=BE,
设BF=BE=x,则EC=EF=2x,OE=3+x,
在Rt△OCE中,OC2+CE2=OE2,
∴32+(2x)2=(3+x)2,
解得x1=0(舍),x2=2,
∴OF=OB﹣FB=1,
在Rt△ODF中,DF===.
21.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,过D作直线DG∥BC.
(1)若∠ACB=80°,则∠ADB= 80° ;∠AEB= 130° .
(2)求证:DE=CD;
(3)求证:DG是⊙O的切线.
【分析】(1)由圆周角定理可得∠ACB=∠ADB=70°,由三角形的内心的性质可得∠AEB=125°;
(2)由三角形的内心的性质可得AE平分∠BAC,BE平分∠ABC,可得∠BAE=∠CAE,∠ABE=∠CBE,由外角的性质可得∠BED=∠DBE,可证DE=CD;
(3)由垂径定理可得OD⊥BC,由平行线的性质可得OD⊥DG,可得结论.
【解答】(1)解:如图,连接OD,
∵=,
∴∠ACB=∠ADB=80°,
∴∠ABC+∠BAC=100°,
∵点E是△ABC的内心,
∴AE平分∠BAC,BE平分∠ABC,
∴∠BAE=∠CAE,∠ABE=∠CBE,
∴∠BAE+∠ABE=50°,
∴∠AEB=130°,
故答案为:80°,130°;
(2)证明:∵∠BAE=∠CAE,
∴=,
∴BD=CD,
∵∠BAE=∠CAE=∠CBD,∠ABE=∠CBE,
∴∠BED=∠BAE+∠ABE=∠CBD+∠CBE=∠DBE,
∴BD=DE,
∴DE=CD;
(3)证明:∵=,
∴OD⊥BC,
∵DG∥BC,
∴OD⊥DG,
又∵OD是半径,
∴DG是⊙O的切线.
22.如图1,在平面直角坐标系中,点A,B的坐标分别为A(8,0)和B(0,6),点P为x轴负半轴上的一个动点,画△ABP的外接圆,圆心为M,连接BM并延长交圆于点C,连接CP.
(1)求证:∠OBP=∠ABC.
(2)当⊙M的直径为14时,求点P的坐标.
(3)如图2,连接OC,求OC的最小值和OC达到最小值时△ABP的外接圆圆心M的坐标.
【分析】(1)如图1,连接AC,由圆周角定理得到:∠BAC=∠BOP=90°,∠ACB=∠APB,所以等角的余角相等:∠OBP=∠ABC.
(2)根据勾股定理求得AB=10,AC=4;由“两角法”证得△OBP∽△ABC,则该相似三角形的对应边成比例(),由此求得线段OP的长度,结合平面直角坐标系得到点P的坐标为;
(3)如图2,记直线AC与y轴的交点为E,由题意知∠OAE=∠OBA=90°﹣∠BAO,当OC最小时,OC⊥AE,此时,通过解直角三角形求得线段OC的长度;易得点C的坐标为根据中点坐标的求法得到点M的坐标即可.
解:(1)如图1,连接AC,
∵BC为⊙M的直径,
∴∠BAC=∠BOP=90°,
∵∠ACB=∠APB,
∴∠OBP+∠APB=∠ABC+∠ACB=90°,
∴∠OBP=∠ABC.
(2)∵∠BAC=90°,A(8,0),B(6,0)
∴OB=6,OA=8,
∴AB=10
∴=
∵∠BOP=∠BAC,∠OBP=∠ABC,
∴△OBP∽△ABC,
∴,
∴=,
∴点P的坐标为;
(3)如图2,记直线AC与y轴的交点为E,
∵AC⊥AB,则∠OAE=∠OBA=90°﹣∠BAO,
当OC最小时,OC⊥AE,
此时,OC=OA sin∠OAE=OA sin∠OBA=.
求得点C的坐标为.
又∵点M为BC的中点
∴,,
∴点M的坐标为.
同课章节目录
