高中数学(创新导学)必修第二册6.3平面向量基本定理及坐标表示A卷(word版含解析)
文档属性
| 名称 | 高中数学(创新导学)必修第二册6.3平面向量基本定理及坐标表示A卷(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 646.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 00:00:00 | ||
图片预览





文档简介
高中数学(创新导学)必修第二册
6.3平面向量基本定理及坐标表示
一、单选题
1.已知向量,.则与的夹角的余弦值为( )
A. B.
C. D.
2.在矩形中,,,若,则与的夹角为( )
A. B. C. D.
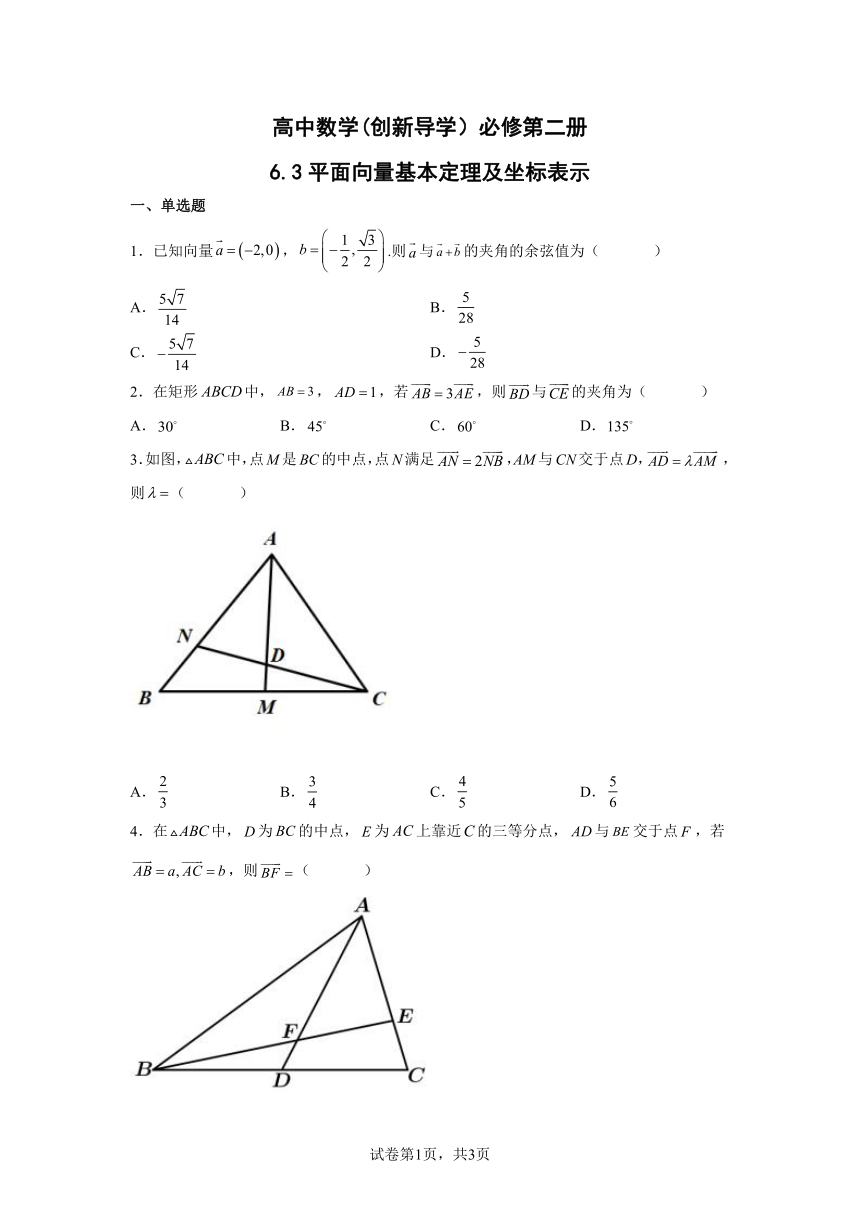
3.如图,中,点M是BC的中点,点N满足,AM与CN交于点D,,则( )
A. B. C. D.
4.在中,为的中点,为上靠近的三等分点,与交于点,若,则( )
A. B.
C. D.
5.已知平面向量,,,则与的夹角为( )
A. B. C. D.
6.已知向量,,,,的夹角为,若存在实数m,使得,则m的取值范围是( )
A. B.
C. D.
7.已知向量,,下列说法正确的是( )
A.,与的夹角不小于 B.,
C.,使得 D.,使得
8.设,向量,,,且,,则( )
A. B. C. D.10
9.骑自行车是一种能有效改善心肺功能的耐力性有氧运动,深受大众喜爱,下图是某一自行车的平面结构示意图,已知图中的圆A(前轮),圆D(后轮)的半径均为,,,均是边长为4的等边三角形,设点P为后轮上的一点,则在骑动该自行车的过程中,的最大值为( )
A.24 B. C. D.
10.设向量,,,其中O为坐标原点,,,若A,B,C三点共线,则的最小值为( )
A.4 B.6 C.8 D.9
11.已知向量,满足,且,则的取值范围是( )
A. B. C. D.
12.在矩形中,,且,则( )
A. B.5 C. D.4
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
13.已知正方形的边长为,为的中点,则______________.
14.在矩形中,已知,(为正常数),为边的中点,是对角线上的动点(含端点),若的取值范围为,则___________.
15.若,且共线,则________.
16.在中,,分别为边,上的点,,,与交于点,设,,则___________.(用,表示)
试卷第页,共页
试卷第页,共页
参考答案:
1.A
【解析】
【分析】
由向量坐标的线性运算求的坐标,应用向量夹角的坐标表示求与的夹角的余弦值.
【详解】
∵,,
∴,则,,
设与的夹角为,则.
故选:A.
2.B
【解析】
【分析】
如图:以为原点,建立如图的直角坐标系,求出各点的坐标以及与的坐标,利用平面向量夹角公式即可求解.
【详解】
如图:以为原点,建立如图的平面直角坐标系,
因为四边形是矩形,,,,
则,,,,则,,
故,
因为,所以,
故选:B.
3.C
【解析】
【分析】
由题设易得,利用平面向量的三点共线定理即可求值.
【详解】
由题设,,又,,
∴,而共线,
∴,可得.
故选:C
4.A
【解析】
【分析】
利用给定条件借助两次共线并结合平面向量基本定理即可用基底表示.
【详解】
在中,为的中点,为上靠近的三等分点,与交于点,
由三点共线得,则存在实数,,
由三点共线得,则存在,使得,又,
因此,,
而与不共线,于是得,解得,
所以.
故选:A
5.C
【解析】
【分析】
求出,由平面向量夹角公式计算的值,结合向量夹角的范围即可求解.
【详解】
由可得,
所以,
因为,所以,
故选:C.
6.C
【解析】
【分析】
根据,可得,即,则只要,求得即可的解.
【详解】
解:由,得,又,所以,
若存在实数m,使得,则,
因为,所以,故.
故选:C.
7.D
【解析】
【分析】
根据向量坐标运算的知识,对选项逐一分析即可.
【详解】
因为向量,,
对于A选项, ,
若与的夹角小于,则,即,解得,
,故A错误;
对于B选项,因为,所以
设其对称轴为,
因为,所以时,单调递减,
当时,单调递增,
所以当时,,
所以,故B错误;
对于C选项,,因为 ,所以,
解得,所以C错误;
对于D选项,,因为,所以,
,,,
所以异号,故,使得,因此D正确.
故选:D
8.C
【解析】
【分析】
根据向量垂直平行关系明确参数,从而可得所求向量的模.
【详解】
∵向量,,,且,,
∴ ,∴,
∴,,,
∴.
故选:C
9.B
【解析】
【分析】
以为轴,为坐标原点建立平面直角坐标系,由圆方程设,写出向量的坐标,由数量积的坐标表示求出数量积,利用三角函数知识得最大值.
【详解】
骑行过程中,相对不动,只有点绕点作圆周运动.
如图,以为轴,为坐标原点建立平面直角坐标系,由题意,,,
圆方程为,设,
则,,
,
易知当时,取得最大值.
故选:B.
10.A
【解析】
【分析】
根据向量共线定理可得,再应用基本不等式“1”的代换求的最小值,注意等号成立条件.
【详解】
由题设,,,A,B,C三点共线,
∴且,则,可得,
∴,当且仅当时等号成立.
∴的最小值为.
故选:A
11.B
【解析】
【分析】
设向量,夹角为,由已知可得,根据数量积的定义以及运算律将其展开化简可得,结合的范围即可得的取值范围.
【详解】
由可得即,
设向量,夹角为,则,
由数量积的定义可得:,
因为,所以,
所以,
当时,显然成立;
当时,可得,
因为,所以,因为,
所以,即,可得,
所以,
所以的取值范围是:,
故选:B.
12.A
【解析】
【分析】
由矩形的性质可得,结合已知条件得,再根据向量对应线段的几何关系,结合平面向量数量积的运算律有即可求值.
【详解】
由,则,即.
又,则,
故.
故选:A.
13.-2
【解析】
【分析】
利用基向量表示向量,再利用向量加法与乘法的分配律,交换律化简,运算即得解
【详解】
【点睛】
本题考查了基向量法在向量数量积运算中的运用,考查了学生转化划归、数学运算的能力
14.1
【解析】
【分析】
以为坐标原点,射线分别为轴非负半轴建立平面直角坐标系,借助平面向量运算即可计算作答.
【详解】
以为坐标原点,射线分别为轴非负半轴建立平面直角坐标系,如图,则,
,,,
有,由得:,
而的取值范围为,于是得,而 m为正数,解得:,
所以.
故答案为:1
15.
【解析】
【分析】
根据共线,可求出的值,从而利用数量积的坐标运算即可求出的值.
【详解】
因为共线,所以,即,
所以,所以,
所以.
故答案为:.
16.
【解析】
【分析】
用,表示,再用向量共线表示出,并由求出,再由求出,然后由与共线即可得解.
【详解】
如图,在中,依题意,,,
因与交于点,则,于是得,,
,,
因,而与不共线,从而有,解得,
所以.
故答案为:
试卷第页,共页
试卷第页,共页
6.3平面向量基本定理及坐标表示
一、单选题
1.已知向量,.则与的夹角的余弦值为( )
A. B.
C. D.
2.在矩形中,,,若,则与的夹角为( )
A. B. C. D.
3.如图,中,点M是BC的中点,点N满足,AM与CN交于点D,,则( )
A. B. C. D.
4.在中,为的中点,为上靠近的三等分点,与交于点,若,则( )
A. B.
C. D.
5.已知平面向量,,,则与的夹角为( )
A. B. C. D.
6.已知向量,,,,的夹角为,若存在实数m,使得,则m的取值范围是( )
A. B.
C. D.
7.已知向量,,下列说法正确的是( )
A.,与的夹角不小于 B.,
C.,使得 D.,使得
8.设,向量,,,且,,则( )
A. B. C. D.10
9.骑自行车是一种能有效改善心肺功能的耐力性有氧运动,深受大众喜爱,下图是某一自行车的平面结构示意图,已知图中的圆A(前轮),圆D(后轮)的半径均为,,,均是边长为4的等边三角形,设点P为后轮上的一点,则在骑动该自行车的过程中,的最大值为( )
A.24 B. C. D.
10.设向量,,,其中O为坐标原点,,,若A,B,C三点共线,则的最小值为( )
A.4 B.6 C.8 D.9
11.已知向量,满足,且,则的取值范围是( )
A. B. C. D.
12.在矩形中,,且,则( )
A. B.5 C. D.4
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
13.已知正方形的边长为,为的中点,则______________.
14.在矩形中,已知,(为正常数),为边的中点,是对角线上的动点(含端点),若的取值范围为,则___________.
15.若,且共线,则________.
16.在中,,分别为边,上的点,,,与交于点,设,,则___________.(用,表示)
试卷第页,共页
试卷第页,共页
参考答案:
1.A
【解析】
【分析】
由向量坐标的线性运算求的坐标,应用向量夹角的坐标表示求与的夹角的余弦值.
【详解】
∵,,
∴,则,,
设与的夹角为,则.
故选:A.
2.B
【解析】
【分析】
如图:以为原点,建立如图的直角坐标系,求出各点的坐标以及与的坐标,利用平面向量夹角公式即可求解.
【详解】
如图:以为原点,建立如图的平面直角坐标系,
因为四边形是矩形,,,,
则,,,,则,,
故,
因为,所以,
故选:B.
3.C
【解析】
【分析】
由题设易得,利用平面向量的三点共线定理即可求值.
【详解】
由题设,,又,,
∴,而共线,
∴,可得.
故选:C
4.A
【解析】
【分析】
利用给定条件借助两次共线并结合平面向量基本定理即可用基底表示.
【详解】
在中,为的中点,为上靠近的三等分点,与交于点,
由三点共线得,则存在实数,,
由三点共线得,则存在,使得,又,
因此,,
而与不共线,于是得,解得,
所以.
故选:A
5.C
【解析】
【分析】
求出,由平面向量夹角公式计算的值,结合向量夹角的范围即可求解.
【详解】
由可得,
所以,
因为,所以,
故选:C.
6.C
【解析】
【分析】
根据,可得,即,则只要,求得即可的解.
【详解】
解:由,得,又,所以,
若存在实数m,使得,则,
因为,所以,故.
故选:C.
7.D
【解析】
【分析】
根据向量坐标运算的知识,对选项逐一分析即可.
【详解】
因为向量,,
对于A选项, ,
若与的夹角小于,则,即,解得,
,故A错误;
对于B选项,因为,所以
设其对称轴为,
因为,所以时,单调递减,
当时,单调递增,
所以当时,,
所以,故B错误;
对于C选项,,因为 ,所以,
解得,所以C错误;
对于D选项,,因为,所以,
,,,
所以异号,故,使得,因此D正确.
故选:D
8.C
【解析】
【分析】
根据向量垂直平行关系明确参数,从而可得所求向量的模.
【详解】
∵向量,,,且,,
∴ ,∴,
∴,,,
∴.
故选:C
9.B
【解析】
【分析】
以为轴,为坐标原点建立平面直角坐标系,由圆方程设,写出向量的坐标,由数量积的坐标表示求出数量积,利用三角函数知识得最大值.
【详解】
骑行过程中,相对不动,只有点绕点作圆周运动.
如图,以为轴,为坐标原点建立平面直角坐标系,由题意,,,
圆方程为,设,
则,,
,
易知当时,取得最大值.
故选:B.
10.A
【解析】
【分析】
根据向量共线定理可得,再应用基本不等式“1”的代换求的最小值,注意等号成立条件.
【详解】
由题设,,,A,B,C三点共线,
∴且,则,可得,
∴,当且仅当时等号成立.
∴的最小值为.
故选:A
11.B
【解析】
【分析】
设向量,夹角为,由已知可得,根据数量积的定义以及运算律将其展开化简可得,结合的范围即可得的取值范围.
【详解】
由可得即,
设向量,夹角为,则,
由数量积的定义可得:,
因为,所以,
所以,
当时,显然成立;
当时,可得,
因为,所以,因为,
所以,即,可得,
所以,
所以的取值范围是:,
故选:B.
12.A
【解析】
【分析】
由矩形的性质可得,结合已知条件得,再根据向量对应线段的几何关系,结合平面向量数量积的运算律有即可求值.
【详解】
由,则,即.
又,则,
故.
故选:A.
13.-2
【解析】
【分析】
利用基向量表示向量,再利用向量加法与乘法的分配律,交换律化简,运算即得解
【详解】
【点睛】
本题考查了基向量法在向量数量积运算中的运用,考查了学生转化划归、数学运算的能力
14.1
【解析】
【分析】
以为坐标原点,射线分别为轴非负半轴建立平面直角坐标系,借助平面向量运算即可计算作答.
【详解】
以为坐标原点,射线分别为轴非负半轴建立平面直角坐标系,如图,则,
,,,
有,由得:,
而的取值范围为,于是得,而 m为正数,解得:,
所以.
故答案为:1
15.
【解析】
【分析】
根据共线,可求出的值,从而利用数量积的坐标运算即可求出的值.
【详解】
因为共线,所以,即,
所以,所以,
所以.
故答案为:.
16.
【解析】
【分析】
用,表示,再用向量共线表示出,并由求出,再由求出,然后由与共线即可得解.
【详解】
如图,在中,依题意,,,
因与交于点,则,于是得,,
,,
因,而与不共线,从而有,解得,
所以.
故答案为:
试卷第页,共页
试卷第页,共页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
