6.4生活中的圆周运动能力提升练(word版含答案)
文档属性
| 名称 | 6.4生活中的圆周运动能力提升练(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 159.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-14 15:31:17 | ||
图片预览



文档简介
2022版高中同步人教版必修第二册 6.4 生活中的圆周运动 能力提升练
一、多选题
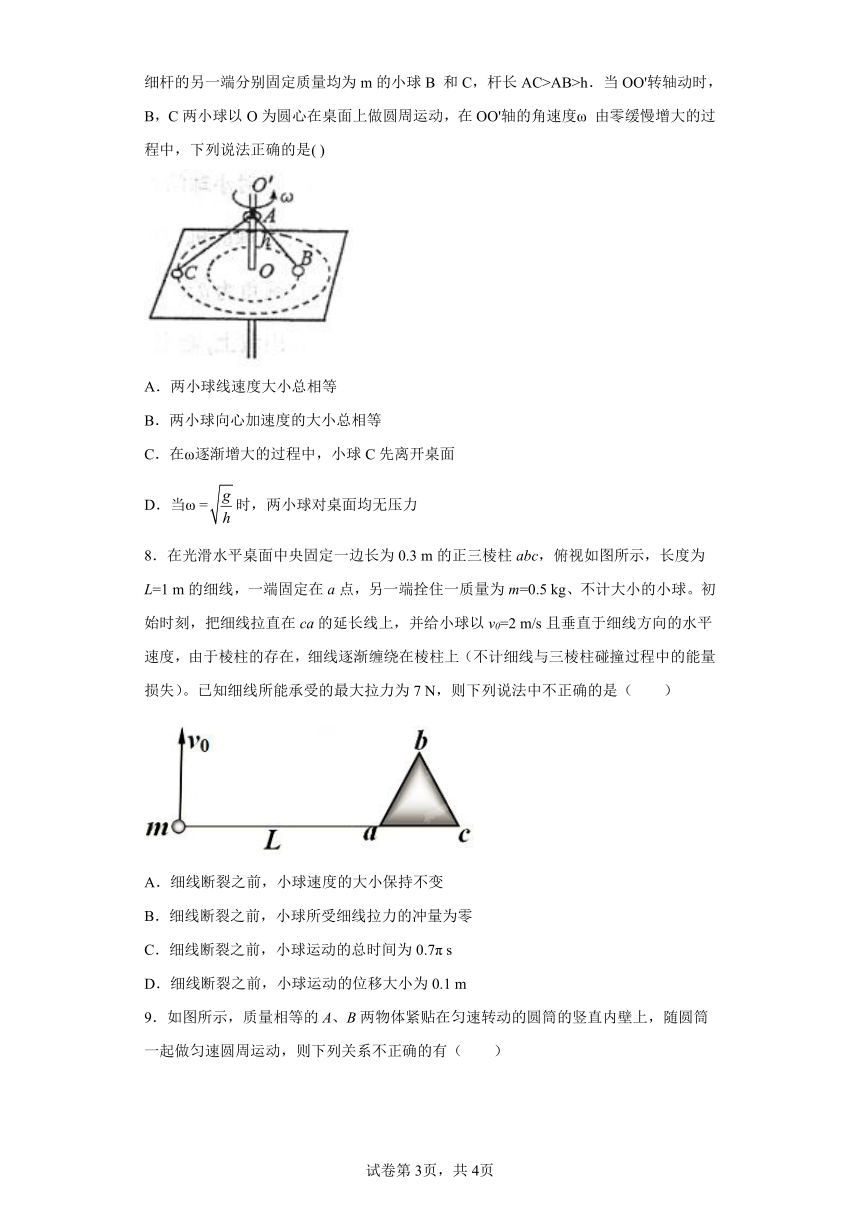
1.在公路转弯处外侧的李先生家门口,三个月内连续发生了八次大卡车的交通事故。经公安部门和交通部门协力调查,画出的现场示意图如图所示。为了避免交通卡车事故再次发生,很多人提出了建议,下列建议中合理的是( )
A.改进路面设计,增大车轮与路面间的摩擦因数
B.改造此段弯路,使弯道内侧高、外侧低
C.把路面的弯道半径改小一点
D.在进入转弯处设立限速标志,提醒司机不要超速转弯
2.如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为R,小球半径为r,重力加速度为g,下列说法正确的是( )
A.若小球通过最高点时对管壁没有作用力,则此时小球速度为v=
B.小球通过最高点时的最小速度vmin=
C.小球在水平线ab以下的管道中运动时,内侧管壁对小球一定无作用力
D.小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力
3.当汽车通过圆弧形凸桥时,下列说法中正确的是( )
A.汽车在桥顶通过时,对桥的压力一定小于汽车的重力
B.汽车通过桥顶时,速度越小,对桥的压力就越小
C.汽车所需的向心力由重力和桥对汽车的支持力来提供
D.汽车所需的向心力一定由重力来提供
4.汽车通过拱形桥时的运动可以看作圆周运动,如图所示。质量为m的汽车以速度v通过半径为R的拱形桥最高点时,下列说法正确的是( )
A.桥对汽车的支持力等于汽车对桥的压力 B.汽车对桥的压力大小为mg
C.桥对汽车的支持力大小为 D.无论汽车的速度有多大,汽车对桥始终有压力
5.有关圆周运动的基本模型,下列说法正确的是( )
A.如图a,汽车通过拱桥的最高点处于超重状态
B.如图b所示是一圆锥摆,增大θ,若保持圆锥的高不变,则圆锥摆的角速度不变
C.如图c,汽车通过凹形桥最低点时不需要限速
D.如图d,汽车在水平路面转弯超过规定速度行驶时,会向外侧发生侧滑
6.如图所示,两个半径不同而内壁光滑的半圆轨道固定于地面,一个小球先后从与球心在同一水平高度的A、B两点由静止开始自由下滑,通过轨道最低点时( )
A.小球对轨道的压力相同
B.小球对两轨道的压力不同
C.此时小球的向心加速度不相等
D.此时小球的向心加速度相等
二、单选题
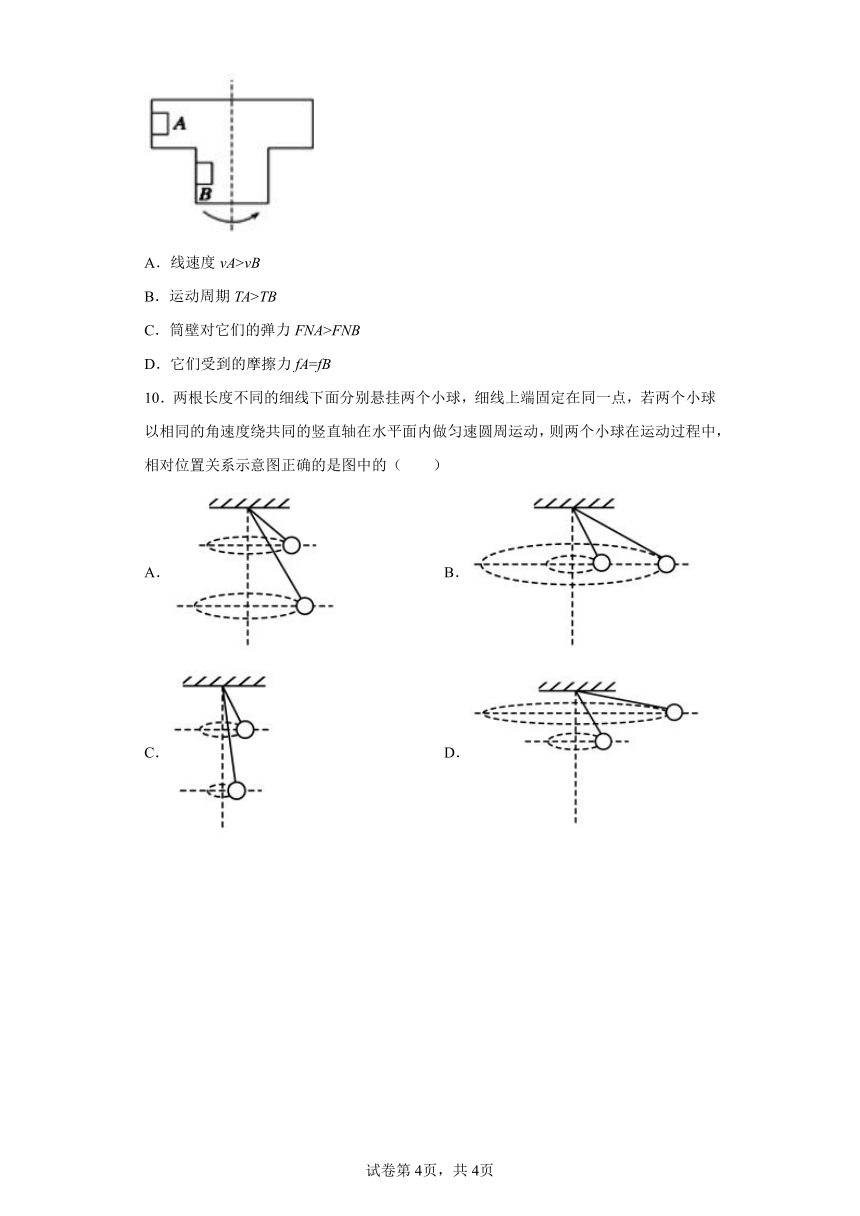
7.如图所示,竖直转轴OO'垂直于光滑水平面,A是距O高h的轴上的一点,A点固定有两铰链.两轻质细杆的一端接到铰链上,并可绕铰链上的光滑轴在竖直面内转动,细杆的另一端分别固定质量均为m的小球B 和C,杆长AC>AB>h.当OO'转轴动时,B,C两小球以O为圆心在桌面上做圆周运动,在OO'轴的角速度ω 由零缓慢增大的过程中,下列说法正确的是( )
A.两小球线速度大小总相等
B.两小球向心加速度的大小总相等
C.在ω逐渐增大的过程中,小球C先离开桌面
D.当ω =时,两小球对桌面均无压力
8.在光滑水平桌面中央固定一边长为0.3 m的正三棱柱abc,俯视如图所示,长度为L=1 m的细线,一端固定在a点,另一端拴住一质量为m=0.5 kg、不计大小的小球。初始时刻,把细线拉直在ca的延长线上,并给小球以v0=2 m/s且垂直于细线方向的水平速度,由于棱柱的存在,细线逐渐缠绕在棱柱上(不计细线与三棱柱碰撞过程中的能量损失)。已知细线所能承受的最大拉力为7 N,则下列说法中不正确的是( )
A.细线断裂之前,小球速度的大小保持不变
B.细线断裂之前,小球所受细线拉力的冲量为零
C.细线断裂之前,小球运动的总时间为0.7π s
D.细线断裂之前,小球运动的位移大小为0.1 m
9.如图所示,质量相等的A、B两物体紧贴在匀速转动的圆筒的竖直内壁上,随圆筒一起做匀速圆周运动,则下列关系不正确的有( )
A.线速度vA>vB
B.运动周期TA>TB
C.筒壁对它们的弹力FNA>FNB
D.它们受到的摩擦力fA=fB
10.两根长度不同的细线下面分别悬挂两个小球,细线上端固定在同一点,若两个小球以相同的角速度绕共同的竖直轴在水平面内做匀速圆周运动,则两个小球在运动过程中,相对位置关系示意图正确的是图中的( )
A. B.
C. D.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.AD
【解析】
【分析】
【详解】
A.在水平路面上拐弯时,靠静摩擦力提供向心力,故可以通过改进路面设计,增大车轮与路面间的摩擦力,A正确;
B.易发生侧翻也可能是路面设计不合理,公路的设计上内侧高外侧低,重力沿斜面方向的分力背离圆心,导致合力不够提供向心力而致;故应改造路面使内侧低,外侧高,B错误;
C.车发生侧翻是因为提供的力不够做圆周运动所需的向心力,发生离心运动;故增大半径可以减小向心力,可以防止侧翻现象,C错误;
D.车发生侧翻是因为提供的力不够做圆周运动所需的向心力,发生离心运动;故减小速度可以减小向心力,可以防止侧翻现象,D正确。
故选AD。
2.AC
【解析】
【详解】
A.若小球通过最高点时对管壁没有作用力,则根据牛顿第二定律有
解得此时小球的速度为
故A正确;
B.由于小球能够受到内侧管壁对其的作用力,所以其通过最高点时的最小速度为0,故B错误;
C.小球在水平线ab以下的管道中运动时,向心力方向指向圆心,由于重力在半径方向的分力始终背离圆心,所以外侧管壁一定对小球有指向圆心的作用力,则小球一定与外侧管壁之间存在挤压,而内侧管壁对小球一定无作用力,故C正确;
D.小球在水平线ab以上的管道中运动且速度较小时,使得小球重力在半径方向的分力大于等于所需的向心力,此时内侧管壁对小球一定有背离圆心的作用力,而外侧管壁对小球无作用力,速度较大时,则对外侧管壁有作用力, 故D错误。
故选AC。
3.AC
【解析】
【分析】
【详解】
CD.汽车通过拱桥时做圆周运动,在最高点,重力和支持力的合力提供向心力,D错误C正确;
AB.由牛顿第二定律得
解得
根据牛顿第三定律,对桥的压力
速度越小,对桥的压力就越大,B错误A正确。
故选AC。
4.AC
【解析】
【详解】
A.根据牛顿第三定律,桥对汽车的支持力与汽车对桥的压力是作用力与反作用力,大小相等,故A正确;
B.汽车对桥的压力小于,故B错误;
C.根据牛顿第二定律
桥对汽车的支持力大小
故C正确;
D.当汽车的速度,重力提供向心力,汽车将要飞起来,汽车对桥没有压力,故D错误。
故选AC。
5.BD
【解析】
【详解】
A.汽车在拱桥最高点,
mg-FN=
知
FN故处于失重状态,故A错误;
B.题图b所示是一圆锥摆,重力和拉力的合力
F=mgtanθ=mω2r
又
r=Lsinθ
得
ω==
故增大θ,但保持圆锥的高不变,角速度不变,故B正确;
C.在凹形桥最低点有
FN-mg=
若速度v很大,则车对桥的压力
FN′=FN=mg+
很大,容易压坏路面,故C错误;
D.汽车在水平路面转弯时,静摩擦力指向内侧,若超速行驶,则静摩擦力达到最大静摩擦力后也不足以充当汽车转弯的向心力,汽车会向外侧发生侧滑,故D正确。
故选BD。
6.AD
【解析】
【详解】
AB.根据机械能守恒定律
到达最低点时
整理得
可知两球对轨道的压力与半径无关,A正确,B错误
CD.在最低点时两种情况受力完全相同,根据牛顿第二定律,加速度也完全相同,因此D正确,C错误。
故选AD。
7.D
【解析】
【分析】
两小球同轴转动,角速度相同,根据v=ωr和a=ω2r比较线速度和向心加速度;当小球恰离开桌面时,根据牛顿第二定律求解临界角速度可判断选项CD.
【详解】
两球转动的角速度相同,根据v=ωr可知两小球线速度大小不相等,根据a=ω2r可知两小球向心加速度的大小也不相等,选项AB错误;当小球恰好离开桌面时满足:(θ为细杆与竖直方向的夹角)解得,可知在ω逐渐增大的过程中,两小球一起离开桌面,即当ω =时,两小球对桌面均无压力,选项C错误,D正确;故选D.
8.BD
【解析】
【分析】
【详解】
A.细线断裂之前,绳子拉力与速度垂直,不做功,不改变小球的速度大小,故小球的速度大小保持不变.故A正确;
B.细线断裂之前,小球所受细线拉力不为零,故拉力的冲量不为零,选项B错误;
C.绳子刚断裂时,拉力大小为7N,由
得此时的半径为
由于小球每转120°半径减小0.3m,则知小球刚好转过一周,细线断裂,则小球运动的总时间为
而
r1=1m,r2=0.7m,r3=0.4m,v0=2m/s,解得
故C正确;
D.小球每转120°半径减小0.3m,细线断裂之前,小球运动的位移大小为1m-0.1m=0.9m.故D错误。
本题选不正确的,故选BD。
9.B
【解析】
【分析】
【详解】
AB.由题分析可知,A、B两物体的角速度相同,周期相同,由v=ωr知,ω相同,则线速度与半径成正比,A的半径大则其线速度大,故A不符题意,B符合题意;
C.两个物体都做匀速圆周运动,由圆筒的弹力提供向心力,则
N=Fn=mω2r
m、ω相等,FN与r成正比,所以可知FNA>FNB;故C不符题意;
D.两个物体竖直方向都没有加速度,受力平衡,所受的摩擦力都等于重力,而两个物体的重力相等,所以可得摩擦力为fA=fB;故D不符题意;
故选B。
10.B
【解析】
【详解】
设细线与竖直方向的夹角为 ,根据牛顿第二定律有
解得
所以两个小球以相同的角速度绕共同的竖直轴在水平面内做匀速圆周运动,则两个小球在运动过程中高度相同,在同一水平面上,所以B正确;ACD错误;
故选B。
答案第1页,共2页
答案第1页,共2页
一、多选题
1.在公路转弯处外侧的李先生家门口,三个月内连续发生了八次大卡车的交通事故。经公安部门和交通部门协力调查,画出的现场示意图如图所示。为了避免交通卡车事故再次发生,很多人提出了建议,下列建议中合理的是( )
A.改进路面设计,增大车轮与路面间的摩擦因数
B.改造此段弯路,使弯道内侧高、外侧低
C.把路面的弯道半径改小一点
D.在进入转弯处设立限速标志,提醒司机不要超速转弯
2.如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为R,小球半径为r,重力加速度为g,下列说法正确的是( )
A.若小球通过最高点时对管壁没有作用力,则此时小球速度为v=
B.小球通过最高点时的最小速度vmin=
C.小球在水平线ab以下的管道中运动时,内侧管壁对小球一定无作用力
D.小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力
3.当汽车通过圆弧形凸桥时,下列说法中正确的是( )
A.汽车在桥顶通过时,对桥的压力一定小于汽车的重力
B.汽车通过桥顶时,速度越小,对桥的压力就越小
C.汽车所需的向心力由重力和桥对汽车的支持力来提供
D.汽车所需的向心力一定由重力来提供
4.汽车通过拱形桥时的运动可以看作圆周运动,如图所示。质量为m的汽车以速度v通过半径为R的拱形桥最高点时,下列说法正确的是( )
A.桥对汽车的支持力等于汽车对桥的压力 B.汽车对桥的压力大小为mg
C.桥对汽车的支持力大小为 D.无论汽车的速度有多大,汽车对桥始终有压力
5.有关圆周运动的基本模型,下列说法正确的是( )
A.如图a,汽车通过拱桥的最高点处于超重状态
B.如图b所示是一圆锥摆,增大θ,若保持圆锥的高不变,则圆锥摆的角速度不变
C.如图c,汽车通过凹形桥最低点时不需要限速
D.如图d,汽车在水平路面转弯超过规定速度行驶时,会向外侧发生侧滑
6.如图所示,两个半径不同而内壁光滑的半圆轨道固定于地面,一个小球先后从与球心在同一水平高度的A、B两点由静止开始自由下滑,通过轨道最低点时( )
A.小球对轨道的压力相同
B.小球对两轨道的压力不同
C.此时小球的向心加速度不相等
D.此时小球的向心加速度相等
二、单选题
7.如图所示,竖直转轴OO'垂直于光滑水平面,A是距O高h的轴上的一点,A点固定有两铰链.两轻质细杆的一端接到铰链上,并可绕铰链上的光滑轴在竖直面内转动,细杆的另一端分别固定质量均为m的小球B 和C,杆长AC>AB>h.当OO'转轴动时,B,C两小球以O为圆心在桌面上做圆周运动,在OO'轴的角速度ω 由零缓慢增大的过程中,下列说法正确的是( )
A.两小球线速度大小总相等
B.两小球向心加速度的大小总相等
C.在ω逐渐增大的过程中,小球C先离开桌面
D.当ω =时,两小球对桌面均无压力
8.在光滑水平桌面中央固定一边长为0.3 m的正三棱柱abc,俯视如图所示,长度为L=1 m的细线,一端固定在a点,另一端拴住一质量为m=0.5 kg、不计大小的小球。初始时刻,把细线拉直在ca的延长线上,并给小球以v0=2 m/s且垂直于细线方向的水平速度,由于棱柱的存在,细线逐渐缠绕在棱柱上(不计细线与三棱柱碰撞过程中的能量损失)。已知细线所能承受的最大拉力为7 N,则下列说法中不正确的是( )
A.细线断裂之前,小球速度的大小保持不变
B.细线断裂之前,小球所受细线拉力的冲量为零
C.细线断裂之前,小球运动的总时间为0.7π s
D.细线断裂之前,小球运动的位移大小为0.1 m
9.如图所示,质量相等的A、B两物体紧贴在匀速转动的圆筒的竖直内壁上,随圆筒一起做匀速圆周运动,则下列关系不正确的有( )
A.线速度vA>vB
B.运动周期TA>TB
C.筒壁对它们的弹力FNA>FNB
D.它们受到的摩擦力fA=fB
10.两根长度不同的细线下面分别悬挂两个小球,细线上端固定在同一点,若两个小球以相同的角速度绕共同的竖直轴在水平面内做匀速圆周运动,则两个小球在运动过程中,相对位置关系示意图正确的是图中的( )
A. B.
C. D.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.AD
【解析】
【分析】
【详解】
A.在水平路面上拐弯时,靠静摩擦力提供向心力,故可以通过改进路面设计,增大车轮与路面间的摩擦力,A正确;
B.易发生侧翻也可能是路面设计不合理,公路的设计上内侧高外侧低,重力沿斜面方向的分力背离圆心,导致合力不够提供向心力而致;故应改造路面使内侧低,外侧高,B错误;
C.车发生侧翻是因为提供的力不够做圆周运动所需的向心力,发生离心运动;故增大半径可以减小向心力,可以防止侧翻现象,C错误;
D.车发生侧翻是因为提供的力不够做圆周运动所需的向心力,发生离心运动;故减小速度可以减小向心力,可以防止侧翻现象,D正确。
故选AD。
2.AC
【解析】
【详解】
A.若小球通过最高点时对管壁没有作用力,则根据牛顿第二定律有
解得此时小球的速度为
故A正确;
B.由于小球能够受到内侧管壁对其的作用力,所以其通过最高点时的最小速度为0,故B错误;
C.小球在水平线ab以下的管道中运动时,向心力方向指向圆心,由于重力在半径方向的分力始终背离圆心,所以外侧管壁一定对小球有指向圆心的作用力,则小球一定与外侧管壁之间存在挤压,而内侧管壁对小球一定无作用力,故C正确;
D.小球在水平线ab以上的管道中运动且速度较小时,使得小球重力在半径方向的分力大于等于所需的向心力,此时内侧管壁对小球一定有背离圆心的作用力,而外侧管壁对小球无作用力,速度较大时,则对外侧管壁有作用力, 故D错误。
故选AC。
3.AC
【解析】
【分析】
【详解】
CD.汽车通过拱桥时做圆周运动,在最高点,重力和支持力的合力提供向心力,D错误C正确;
AB.由牛顿第二定律得
解得
根据牛顿第三定律,对桥的压力
速度越小,对桥的压力就越大,B错误A正确。
故选AC。
4.AC
【解析】
【详解】
A.根据牛顿第三定律,桥对汽车的支持力与汽车对桥的压力是作用力与反作用力,大小相等,故A正确;
B.汽车对桥的压力小于,故B错误;
C.根据牛顿第二定律
桥对汽车的支持力大小
故C正确;
D.当汽车的速度,重力提供向心力,汽车将要飞起来,汽车对桥没有压力,故D错误。
故选AC。
5.BD
【解析】
【详解】
A.汽车在拱桥最高点,
mg-FN=
知
FN
B.题图b所示是一圆锥摆,重力和拉力的合力
F=mgtanθ=mω2r
又
r=Lsinθ
得
ω==
故增大θ,但保持圆锥的高不变,角速度不变,故B正确;
C.在凹形桥最低点有
FN-mg=
若速度v很大,则车对桥的压力
FN′=FN=mg+
很大,容易压坏路面,故C错误;
D.汽车在水平路面转弯时,静摩擦力指向内侧,若超速行驶,则静摩擦力达到最大静摩擦力后也不足以充当汽车转弯的向心力,汽车会向外侧发生侧滑,故D正确。
故选BD。
6.AD
【解析】
【详解】
AB.根据机械能守恒定律
到达最低点时
整理得
可知两球对轨道的压力与半径无关,A正确,B错误
CD.在最低点时两种情况受力完全相同,根据牛顿第二定律,加速度也完全相同,因此D正确,C错误。
故选AD。
7.D
【解析】
【分析】
两小球同轴转动,角速度相同,根据v=ωr和a=ω2r比较线速度和向心加速度;当小球恰离开桌面时,根据牛顿第二定律求解临界角速度可判断选项CD.
【详解】
两球转动的角速度相同,根据v=ωr可知两小球线速度大小不相等,根据a=ω2r可知两小球向心加速度的大小也不相等,选项AB错误;当小球恰好离开桌面时满足:(θ为细杆与竖直方向的夹角)解得,可知在ω逐渐增大的过程中,两小球一起离开桌面,即当ω =时,两小球对桌面均无压力,选项C错误,D正确;故选D.
8.BD
【解析】
【分析】
【详解】
A.细线断裂之前,绳子拉力与速度垂直,不做功,不改变小球的速度大小,故小球的速度大小保持不变.故A正确;
B.细线断裂之前,小球所受细线拉力不为零,故拉力的冲量不为零,选项B错误;
C.绳子刚断裂时,拉力大小为7N,由
得此时的半径为
由于小球每转120°半径减小0.3m,则知小球刚好转过一周,细线断裂,则小球运动的总时间为
而
r1=1m,r2=0.7m,r3=0.4m,v0=2m/s,解得
故C正确;
D.小球每转120°半径减小0.3m,细线断裂之前,小球运动的位移大小为1m-0.1m=0.9m.故D错误。
本题选不正确的,故选BD。
9.B
【解析】
【分析】
【详解】
AB.由题分析可知,A、B两物体的角速度相同,周期相同,由v=ωr知,ω相同,则线速度与半径成正比,A的半径大则其线速度大,故A不符题意,B符合题意;
C.两个物体都做匀速圆周运动,由圆筒的弹力提供向心力,则
N=Fn=mω2r
m、ω相等,FN与r成正比,所以可知FNA>FNB;故C不符题意;
D.两个物体竖直方向都没有加速度,受力平衡,所受的摩擦力都等于重力,而两个物体的重力相等,所以可得摩擦力为fA=fB;故D不符题意;
故选B。
10.B
【解析】
【详解】
设细线与竖直方向的夹角为 ,根据牛顿第二定律有
解得
所以两个小球以相同的角速度绕共同的竖直轴在水平面内做匀速圆周运动,则两个小球在运动过程中高度相同,在同一水平面上,所以B正确;ACD错误;
故选B。
答案第1页,共2页
答案第1页,共2页
