人教版八年级数学上册11.3.2多边形的内角和 教案
文档属性
| 名称 | 人教版八年级数学上册11.3.2多边形的内角和 教案 | 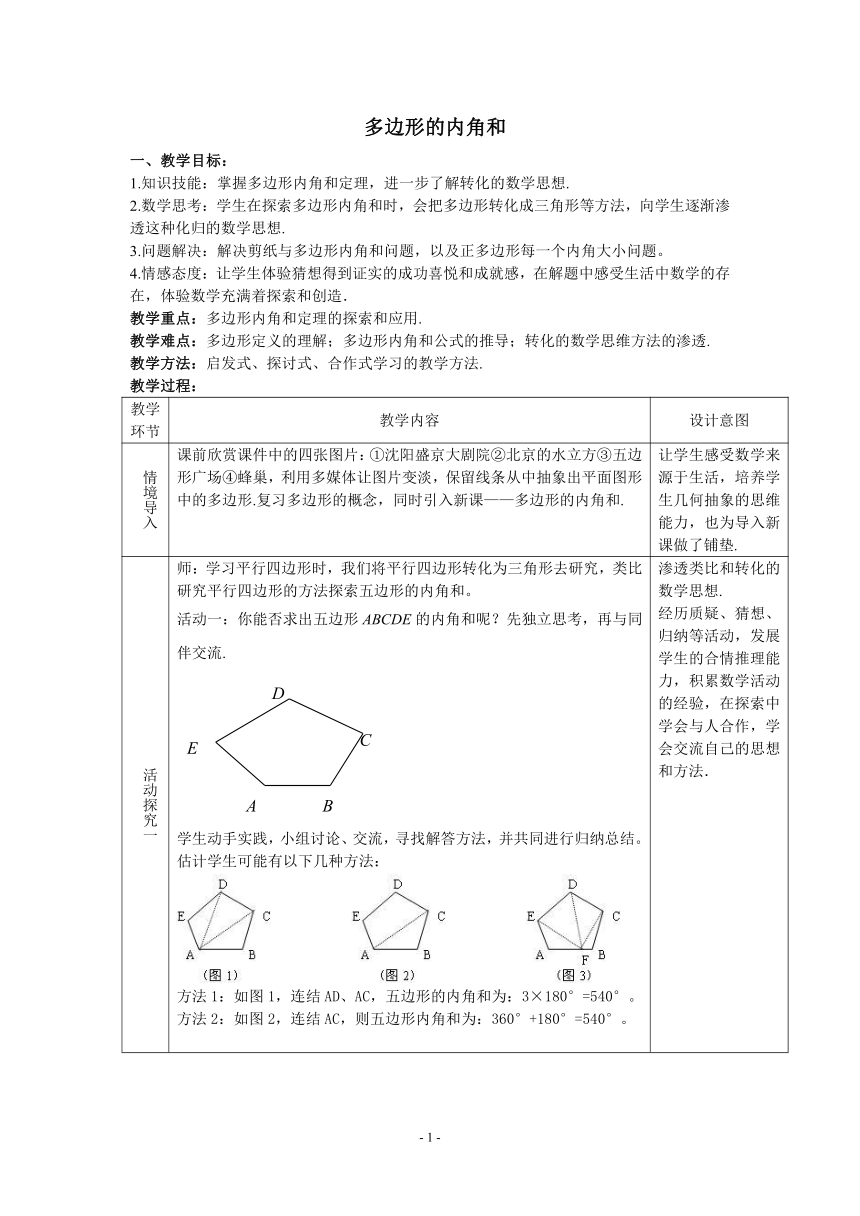 | |
| 格式 | doc | ||
| 文件大小 | 89.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 09:42:54 | ||
图片预览

文档简介
多边形的内角和
一、教学目标:
1.知识技能:掌握多边形内角和定理,进一步了解转化的数学思想.
2.数学思考:学生在探索多边形内角和时,会把多边形转化成三角形等方法,向学生逐渐渗透这种化归的数学思想.
3.问题解决:解决剪纸与多边形内角和问题,以及正多边形每一个内角大小问题。
4.情感态度:让学生体验猜想得到证实的成功喜悦和成就感,在解题中感受生活中数学的存在,体验数学充满着探索和创造.
教学重点:多边形内角和定理的探索和应用.
教学难点:多边形定义的理解;多边形内角和公式的推导;转化的数学思维方法的渗透.
教学方法:启发式、探讨式、合作式学习的教学方法.
教学过程:
教学环节 教学内容 设计意图
情境导入 课前欣赏课件中的四张图片:①沈阳盛京大剧院②北京的水立方③五边形广场④蜂巢,利用多媒体让图片变淡,保留线条从中抽象出平面图形中的多边形.复习多边形的概念,同时引入新课——多边形的内角和. 让学生感受数学来源于生活,培养学生几何抽象的思维能力,也为导入新课做了铺垫.
活动探究一 师:学习平行四边形时,我们将平行四边形转化为三角形去研究,类比研究平行四边形的方法探索五边形的内角和。活动一:你能否求出五边形ABCDE的内角和呢?先独立思考,再与同伴交流.学生动手实践,小组讨论、交流,寻找解答方法,并共同进行归纳总结。估计学生可能有以下几种方法:方法1:如图1,连结AD、AC,五边形的内角和为:3×180°=540°。方法2:如图2,连结AC,则五边形内角和为:360°+180°=540°。 渗透类比和转化的数学思想.经历质疑、猜想、归纳等活动,发展学生的合情推理能力,积累数学活动的经验,在探索中学会与人合作,学会交流自己的思想和方法.
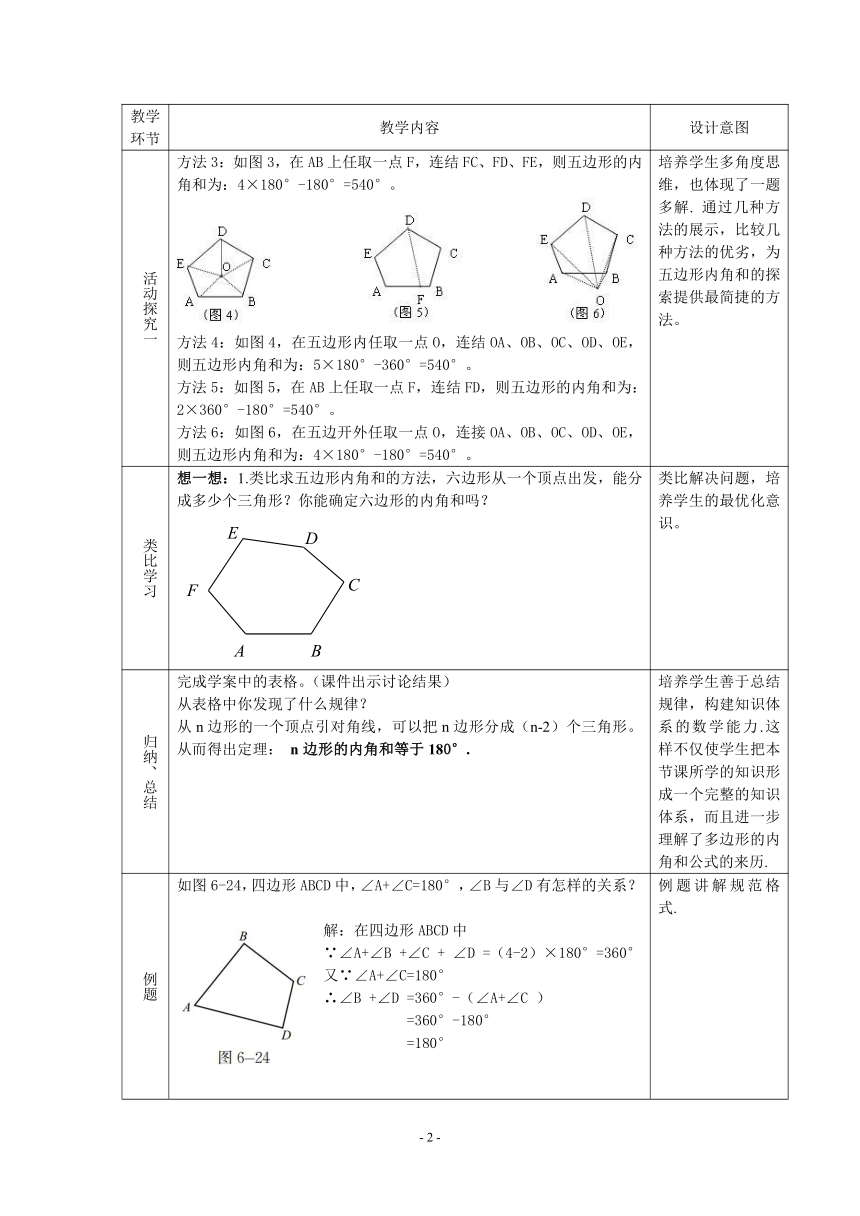
活动探究一 方法3:如图3,在AB上任取一点F,连结FC、FD、FE,则五边形的内角和为:4×180°-180°=540°。方法4:如图4,在五边形内任取一点O,连结OA、OB、OC、OD、OE,则五边形内角和为:5×180°-360°=540°。方法5:如图5,在AB上任取一点F,连结FD,则五边形的内角和为:2×360°-180°=540°。方法6:如图6,在五边开外任取一点O,连接OA、OB、OC、OD、OE,则五边形内角和为:4×180°-180°=540°。 培养学生多角度思维,也体现了一题多解. 通过几种方法的展示,比较几种方法的优劣,为五边形内角和的探索提供最简捷的方法。
类比学习 想一想:1.类比求五边形内角和的方法,六边形从一个顶点出发,能分成多少个三角形?你能确定六边形的内角和吗? 类比解决问题,培养学生的最优化意识。
归纳、总结 完成学案中的表格。(课件出示讨论结果)从表格中你发现了什么规律?从n边形的一个顶点引对角线,可以把n边形分成(n-2)个三角形。从而得出定理: n边形的内角和等于180°. 培养学生善于总结规律,构建知识体系的数学能力.这样不仅使学生把本节课所学的知识形成一个完整的知识体系,而且进一步理解了多边形的内角和公式的来历.
例题 如图6-24,四边形ABCD中,∠A+∠C=180°,∠B与∠D有怎样的关系?解:在四边形ABCD中∵∠A+∠B +∠C + ∠D =(4-2)×180°=360°又∵∠A+∠C=180°∴∠B +∠D =360°-(∠A+∠C )=360°-180°=180° 例题讲解规范格式.
随堂练习 1.一个多边形的内角和为1440°,则它是几边形?2.正多边形定义:在平面内,每个内角都 、每条边也都 的多边形叫做正多边形。3.正三角形(等边三角形)、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度? 4.小彬求出一个正多边形的一个内角为145°它的计算正确吗? 学会用方程的思想解决内角和问题.不仅巩固了多边形内角和公式的应用,又进一步理解了正多边形定义.学会正多边形的每一个内角的求法让学生知道多边形的边只能是大于或等于3的自然数.及检验解的合理性.
活动探究二 活动二:剪掉一张长方形ABCD纸片的一个角后,纸片还剩几个角 这个多边形的内角和是多少度 与同伴交流. (几何画板板演示三种情况)①截线不经过任意顶点,纸片剩5个角,内角和为(5-2)×180°=540°②截线经过一个顶点,纸片剩4个角,内角和为(4-2)×180°=360°③截线经过两个顶点,纸片剩3个角,内角和为180°. 引导学生在探究实践的过程中,真正理解和掌握数学的知识、技能和数学思想方法,增强空间观念及数学思考能力的培养,并获得数学活动经验.培养学生分类讨论的数学思想.学会分类讨论要依据同一标准划分.
小结 1.提问学生.2.教师引导学生画出思维导图. 培养学生的归纳、总结能力
作业 略
板书设计
课后反思:
我在思考课堂上如何促进学生在主动、探究、合作、实践中学习数学、学好数学,突出新教材的优势呢?在这节课中我做了大胆的尝试和探索,首先,这节课师生教与学活动是建立在学生的认知发展水平和已有的经验基础上,教师充分激发学生的学习兴趣和积极性,向学生提供了从事数学活动的机会,构建了学生自主探究、合作实践与交流的平台;教师较好地引导学生在探究实践的过程中,真正理解和掌握数学的知识、技能和数学思想方法,增强空间观念及数学思考能力的培养,并获得数学活动经验;其次,这节课的学习内容,通过创设情境问题得以构建和发展,体现了新课程目标理念的开放性原则;第三,这节课教师恰当的评价学生的学习过程,不仅关注了学生在学习过程中表现的行为、态度情感,更关注对学生激励评价及学生的自我评价感受。
当然也有不足之处:1.节课给学生提供的探究思考与交流的时间空间不足,展示交流的机会不够充分,有的同学没有表现的机会。2.本节课学生小组活动的准备、具体实施、归纳交流、评价等环节设计不够完善。
A
B
D
C
E
A
B
D
C
E
F
A
C
B
D
n边形内角和公式
三角形内角和
探究五边形内角和
六边形内角和
6.4 探索多边形的内角和
定理:n边形的内角和等于(n—2)·180°
例题讲解 随堂练习
PAGE
- 1 -
一、教学目标:
1.知识技能:掌握多边形内角和定理,进一步了解转化的数学思想.
2.数学思考:学生在探索多边形内角和时,会把多边形转化成三角形等方法,向学生逐渐渗透这种化归的数学思想.
3.问题解决:解决剪纸与多边形内角和问题,以及正多边形每一个内角大小问题。
4.情感态度:让学生体验猜想得到证实的成功喜悦和成就感,在解题中感受生活中数学的存在,体验数学充满着探索和创造.
教学重点:多边形内角和定理的探索和应用.
教学难点:多边形定义的理解;多边形内角和公式的推导;转化的数学思维方法的渗透.
教学方法:启发式、探讨式、合作式学习的教学方法.
教学过程:
教学环节 教学内容 设计意图
情境导入 课前欣赏课件中的四张图片:①沈阳盛京大剧院②北京的水立方③五边形广场④蜂巢,利用多媒体让图片变淡,保留线条从中抽象出平面图形中的多边形.复习多边形的概念,同时引入新课——多边形的内角和. 让学生感受数学来源于生活,培养学生几何抽象的思维能力,也为导入新课做了铺垫.
活动探究一 师:学习平行四边形时,我们将平行四边形转化为三角形去研究,类比研究平行四边形的方法探索五边形的内角和。活动一:你能否求出五边形ABCDE的内角和呢?先独立思考,再与同伴交流.学生动手实践,小组讨论、交流,寻找解答方法,并共同进行归纳总结。估计学生可能有以下几种方法:方法1:如图1,连结AD、AC,五边形的内角和为:3×180°=540°。方法2:如图2,连结AC,则五边形内角和为:360°+180°=540°。 渗透类比和转化的数学思想.经历质疑、猜想、归纳等活动,发展学生的合情推理能力,积累数学活动的经验,在探索中学会与人合作,学会交流自己的思想和方法.
活动探究一 方法3:如图3,在AB上任取一点F,连结FC、FD、FE,则五边形的内角和为:4×180°-180°=540°。方法4:如图4,在五边形内任取一点O,连结OA、OB、OC、OD、OE,则五边形内角和为:5×180°-360°=540°。方法5:如图5,在AB上任取一点F,连结FD,则五边形的内角和为:2×360°-180°=540°。方法6:如图6,在五边开外任取一点O,连接OA、OB、OC、OD、OE,则五边形内角和为:4×180°-180°=540°。 培养学生多角度思维,也体现了一题多解. 通过几种方法的展示,比较几种方法的优劣,为五边形内角和的探索提供最简捷的方法。
类比学习 想一想:1.类比求五边形内角和的方法,六边形从一个顶点出发,能分成多少个三角形?你能确定六边形的内角和吗? 类比解决问题,培养学生的最优化意识。
归纳、总结 完成学案中的表格。(课件出示讨论结果)从表格中你发现了什么规律?从n边形的一个顶点引对角线,可以把n边形分成(n-2)个三角形。从而得出定理: n边形的内角和等于180°. 培养学生善于总结规律,构建知识体系的数学能力.这样不仅使学生把本节课所学的知识形成一个完整的知识体系,而且进一步理解了多边形的内角和公式的来历.
例题 如图6-24,四边形ABCD中,∠A+∠C=180°,∠B与∠D有怎样的关系?解:在四边形ABCD中∵∠A+∠B +∠C + ∠D =(4-2)×180°=360°又∵∠A+∠C=180°∴∠B +∠D =360°-(∠A+∠C )=360°-180°=180° 例题讲解规范格式.
随堂练习 1.一个多边形的内角和为1440°,则它是几边形?2.正多边形定义:在平面内,每个内角都 、每条边也都 的多边形叫做正多边形。3.正三角形(等边三角形)、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度? 4.小彬求出一个正多边形的一个内角为145°它的计算正确吗? 学会用方程的思想解决内角和问题.不仅巩固了多边形内角和公式的应用,又进一步理解了正多边形定义.学会正多边形的每一个内角的求法让学生知道多边形的边只能是大于或等于3的自然数.及检验解的合理性.
活动探究二 活动二:剪掉一张长方形ABCD纸片的一个角后,纸片还剩几个角 这个多边形的内角和是多少度 与同伴交流. (几何画板板演示三种情况)①截线不经过任意顶点,纸片剩5个角,内角和为(5-2)×180°=540°②截线经过一个顶点,纸片剩4个角,内角和为(4-2)×180°=360°③截线经过两个顶点,纸片剩3个角,内角和为180°. 引导学生在探究实践的过程中,真正理解和掌握数学的知识、技能和数学思想方法,增强空间观念及数学思考能力的培养,并获得数学活动经验.培养学生分类讨论的数学思想.学会分类讨论要依据同一标准划分.
小结 1.提问学生.2.教师引导学生画出思维导图. 培养学生的归纳、总结能力
作业 略
板书设计
课后反思:
我在思考课堂上如何促进学生在主动、探究、合作、实践中学习数学、学好数学,突出新教材的优势呢?在这节课中我做了大胆的尝试和探索,首先,这节课师生教与学活动是建立在学生的认知发展水平和已有的经验基础上,教师充分激发学生的学习兴趣和积极性,向学生提供了从事数学活动的机会,构建了学生自主探究、合作实践与交流的平台;教师较好地引导学生在探究实践的过程中,真正理解和掌握数学的知识、技能和数学思想方法,增强空间观念及数学思考能力的培养,并获得数学活动经验;其次,这节课的学习内容,通过创设情境问题得以构建和发展,体现了新课程目标理念的开放性原则;第三,这节课教师恰当的评价学生的学习过程,不仅关注了学生在学习过程中表现的行为、态度情感,更关注对学生激励评价及学生的自我评价感受。
当然也有不足之处:1.节课给学生提供的探究思考与交流的时间空间不足,展示交流的机会不够充分,有的同学没有表现的机会。2.本节课学生小组活动的准备、具体实施、归纳交流、评价等环节设计不够完善。
A
B
D
C
E
A
B
D
C
E
F
A
C
B
D
n边形内角和公式
三角形内角和
探究五边形内角和
六边形内角和
6.4 探索多边形的内角和
定理:n边形的内角和等于(n—2)·180°
例题讲解 随堂练习
PAGE
- 1 -
