人教版七年级数学下册5.3 平行线的判定与性质(复习课)教案
文档属性
| 名称 | 人教版七年级数学下册5.3 平行线的判定与性质(复习课)教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 179.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 00:00:00 | ||
图片预览


文档简介
平行线的判定与性质(复习课)
学习目标:
1、复习平行线的判定和性质,体会几何说理的过程。灵活运用平行线的判定和性质,提高分析和解决问题的能力。
2、通过自主探索与合作交流的方式掌握本节内容。
3、激发学生学习数学的兴趣,体会合作学习的快乐与成功。
学习重点、难点:
重点: 掌握平行线的判定和性质之间的区别与联系。
平行线的判定和性质的灵活运用。
平行线中的几种基本图形的变式引伸
难点:平行线的判定和性质的灵活运用。
平行线中的几种基本图形的一题多解的解题方法。
教学过程:
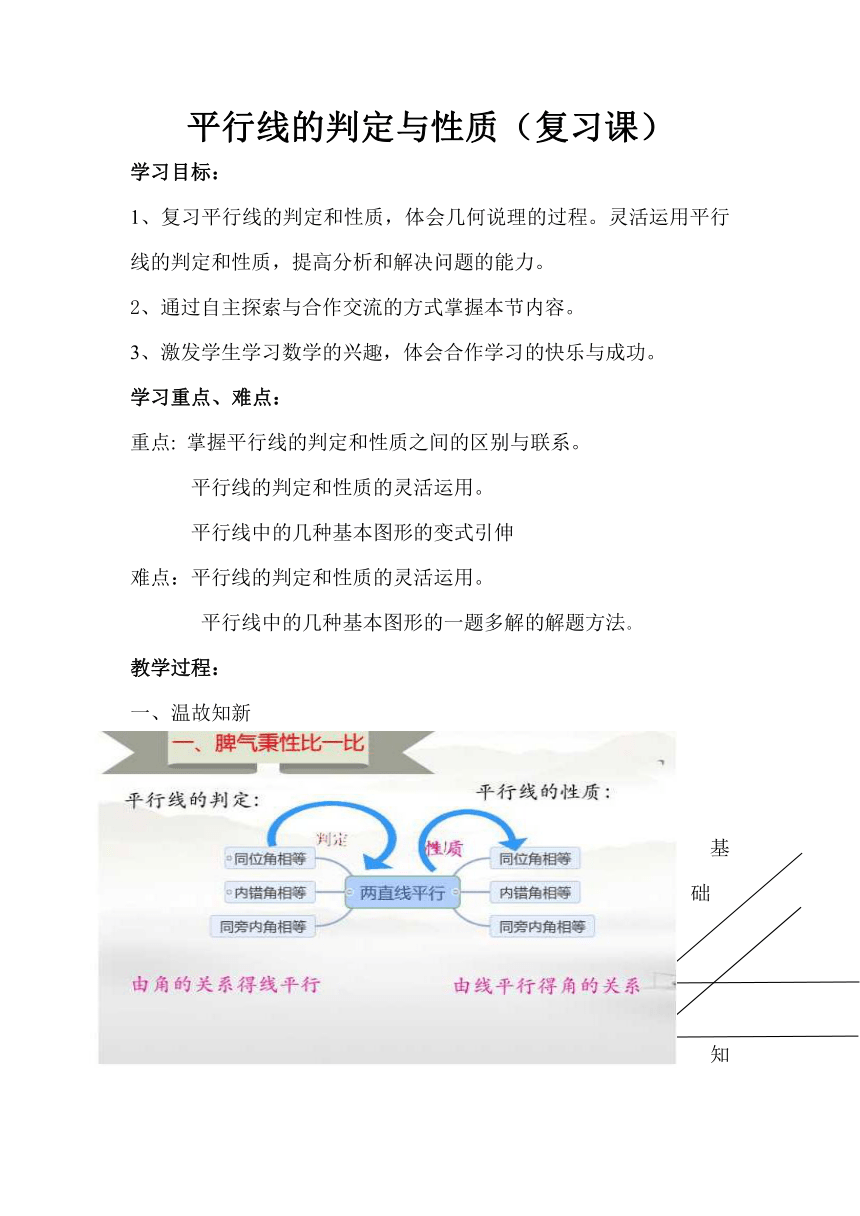
一、温故知新
基础知识训练
1.如图∵∠1=∠2,
∴_______∥________( )。
∵∠2=∠3,
∴_______∥______( )。
析:通过简单的填空练习,整理平行线的判定的方法
①同位角相等,两直线平行
= 2 \* GB3 ②内错角相等,两直线平行
③同旁内角互补,两直线平行
特别:强调同位角、内错角、同旁内角的识别
(就题目中的角说明是哪两条直线被哪条直线所截产生的)
2、如图
∵_______∥________
∴∠3=∠4,( )。
∵_______∥______
∴∠1+∠5=
( )。
分析:通过简单的填空练习,整理平行线的性质定理
①两直线平行,同位角相等
②两直线平行,内错角相等
③两直线平行,同旁内角互补
2、兄弟二人玩一玩
例1:如图所示:AD∥BC,∠A=∠C,试说明AB∥DC.
解:∵ AD//BC(已知)
∴ ∠A=∠ABF(两直线平行,内错角相等)
又∵∠A=∠C (已知)
∴ ∠ABF=∠C (等量代换)
∴ AB∥DC (同位角相等,两直线平行)
思考1:如图所示:AB∥DC,∠A=∠C,试说明 AD∥BC
∵ AB//DC(已知)
∴ ∠C=∠ABF (两直线平行,同位角相等)
又∵∠A=∠C (已知)
∴ ∠ABF=∠A(等量代换)
∴ AD∥BC(内错角相等,两直线平行)
思考2:如图,点E为DF上的点,点B为AC上的点,
∠1= ∠2, ∠C= ∠D,求证:DF ∥AC
思考3:如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,试问:∠A与∠F相等吗?请说出你的理由。
思考4:如图,已知∠A=∠F,∠C=∠D,求证:BD//CE.
3、判定和性质手牵手
例2:如图,已知AB∥CD, ∠1=∠2,
求证∠E=∠F.
∵AB∥CD(已知)
∴ ∠BAD=∠ADC(两直线平行,内错角相等)
又∵∠1=∠2 (已知)
∴ ∠3=∠4(等式的性质)
∴ AF∥DE(内错角相等,两直线平行)
∴ ∠E=∠F(两直线平行,内错角相等)
思考1:如图,已知∠E=∠F, ∠1=∠2,求证 AB∥CD .
学生独立自主练习
思考2:如图,已知AB∥CD, ∠E=∠F,求证∠1=∠2.
学生独立自主练习
4、同心协力来总结
(1)平行线的判定与性质的区别?
(2)在解决具体问题过程中,何时使用平行线的判定,何时使用平行线的性质?
(3)当已知条件中两个角没有特殊位置关系时,怎样处理?
(4)你体会到了什么数学思想?
五、布置作业
练习册
B
D
2
1
C
A
3
F
E
E
C
5
1
A
O
3
2
4
D
F
B
A
E
D
F
B
C
A
E
D
F
B
C
3
2
1
D
E
F
A
B
C
3
2
1
D
E
F
A
B
C
3
2
1
D
E
F
A
B
C
F
1
E
D
B
A
2
C
)
(
3
4
学习目标:
1、复习平行线的判定和性质,体会几何说理的过程。灵活运用平行线的判定和性质,提高分析和解决问题的能力。
2、通过自主探索与合作交流的方式掌握本节内容。
3、激发学生学习数学的兴趣,体会合作学习的快乐与成功。
学习重点、难点:
重点: 掌握平行线的判定和性质之间的区别与联系。
平行线的判定和性质的灵活运用。
平行线中的几种基本图形的变式引伸
难点:平行线的判定和性质的灵活运用。
平行线中的几种基本图形的一题多解的解题方法。
教学过程:
一、温故知新
基础知识训练
1.如图∵∠1=∠2,
∴_______∥________( )。
∵∠2=∠3,
∴_______∥______( )。
析:通过简单的填空练习,整理平行线的判定的方法
①同位角相等,两直线平行
= 2 \* GB3 ②内错角相等,两直线平行
③同旁内角互补,两直线平行
特别:强调同位角、内错角、同旁内角的识别
(就题目中的角说明是哪两条直线被哪条直线所截产生的)
2、如图
∵_______∥________
∴∠3=∠4,( )。
∵_______∥______
∴∠1+∠5=
( )。
分析:通过简单的填空练习,整理平行线的性质定理
①两直线平行,同位角相等
②两直线平行,内错角相等
③两直线平行,同旁内角互补
2、兄弟二人玩一玩
例1:如图所示:AD∥BC,∠A=∠C,试说明AB∥DC.
解:∵ AD//BC(已知)
∴ ∠A=∠ABF(两直线平行,内错角相等)
又∵∠A=∠C (已知)
∴ ∠ABF=∠C (等量代换)
∴ AB∥DC (同位角相等,两直线平行)
思考1:如图所示:AB∥DC,∠A=∠C,试说明 AD∥BC
∵ AB//DC(已知)
∴ ∠C=∠ABF (两直线平行,同位角相等)
又∵∠A=∠C (已知)
∴ ∠ABF=∠A(等量代换)
∴ AD∥BC(内错角相等,两直线平行)
思考2:如图,点E为DF上的点,点B为AC上的点,
∠1= ∠2, ∠C= ∠D,求证:DF ∥AC
思考3:如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,试问:∠A与∠F相等吗?请说出你的理由。
思考4:如图,已知∠A=∠F,∠C=∠D,求证:BD//CE.
3、判定和性质手牵手
例2:如图,已知AB∥CD, ∠1=∠2,
求证∠E=∠F.
∵AB∥CD(已知)
∴ ∠BAD=∠ADC(两直线平行,内错角相等)
又∵∠1=∠2 (已知)
∴ ∠3=∠4(等式的性质)
∴ AF∥DE(内错角相等,两直线平行)
∴ ∠E=∠F(两直线平行,内错角相等)
思考1:如图,已知∠E=∠F, ∠1=∠2,求证 AB∥CD .
学生独立自主练习
思考2:如图,已知AB∥CD, ∠E=∠F,求证∠1=∠2.
学生独立自主练习
4、同心协力来总结
(1)平行线的判定与性质的区别?
(2)在解决具体问题过程中,何时使用平行线的判定,何时使用平行线的性质?
(3)当已知条件中两个角没有特殊位置关系时,怎样处理?
(4)你体会到了什么数学思想?
五、布置作业
练习册
B
D
2
1
C
A
3
F
E
E
C
5
1
A
O
3
2
4
D
F
B
A
E
D
F
B
C
A
E
D
F
B
C
3
2
1
D
E
F
A
B
C
3
2
1
D
E
F
A
B
C
3
2
1
D
E
F
A
B
C
F
1
E
D
B
A
2
C
)
(
3
4
