华东师大版八年级下册数学 第18章 平行四边形 复习课(教案)
文档属性
| 名称 | 华东师大版八年级下册数学 第18章 平行四边形 复习课(教案) |

|
|
| 格式 | docx | ||
| 文件大小 | 170.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 00:00:00 | ||
图片预览

文档简介
平行四边形复习教学设计
复习目标
理解平行四边形的概念、掌握其性质和判定.
运用平行四边形的知识解决相关的证明问题和计算问题
知识点
1.平行四边形的定义
两组对边分别平行的四边形叫平行四边形.
2.平行四边形的性质
(1)两组对边分别平行,即AB∥CD, AD∥BC.
(2)两组对边分别相等,即AB=CD, AD=BC.
(3).两组对角分别相等,即∠ABC=∠ADC, ∠BAD=∠BCD;
(4)对角线互相平分,即OA=OC,OB=OD.
平行四边形是中心对称图形.
平行四边形的判定
分别平行的四边形是平行四边形.
两组对边
边 分别相等的四边形是平行四边形.
一组对边: 平行且相等的四边形是平行四边形.
对角线:对角线互相平分的四边形是平行四边形.
基础训练
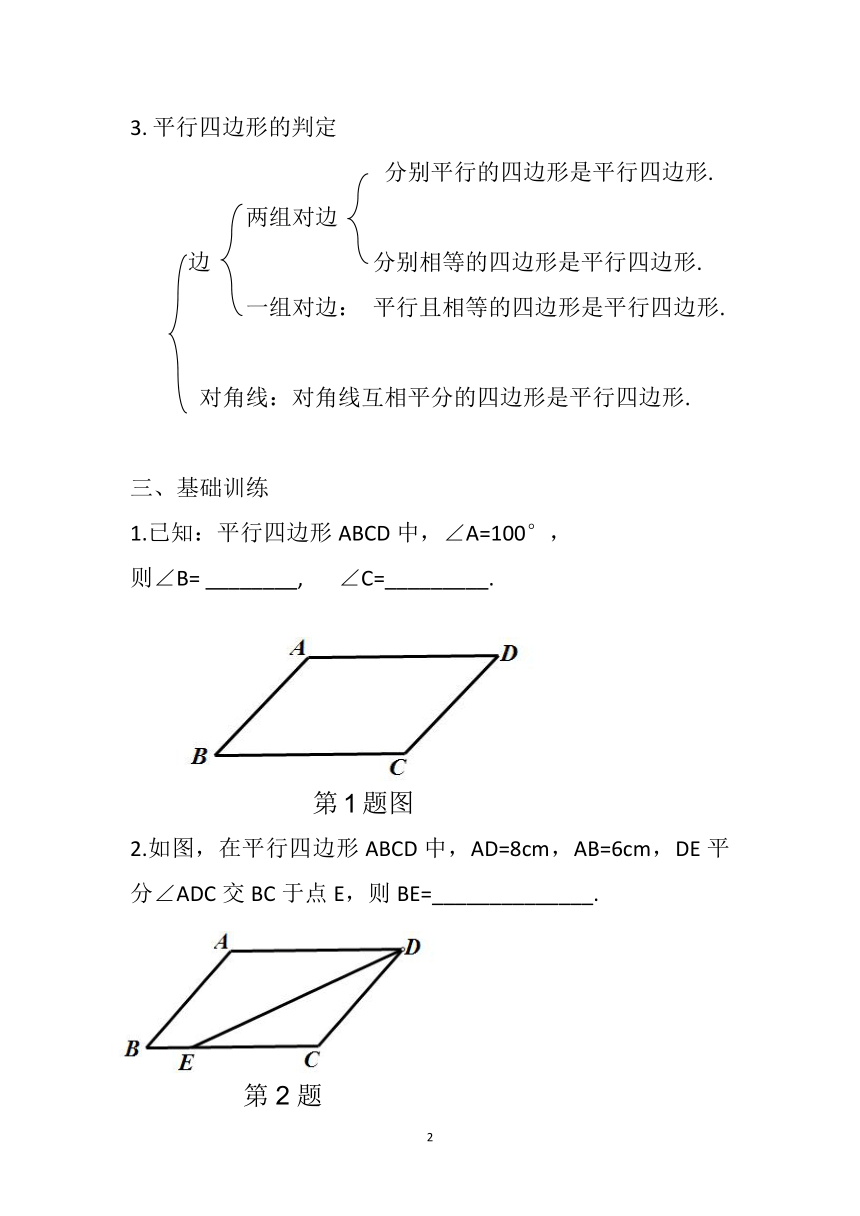
1.已知:平行四边形ABCD中,∠A=100°,
则∠B= ________, ∠C=_________.
2.如图,在平行四边形ABCD中,AD=8cm,AB=6cm,DE平分∠ADC交BC于点E,则BE=______________.
3.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,若AC+BD=36,AB=10,则△AOB的周长为______________.
4.如图,四边形ABCD的对角线相交于点O,若AB//CD,请你添加一个条件____________,使得四边形ABCD为平行四边形.
典型例题
例1 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且E、F、G、H分别是OA、OB、OC、OD的中点.请判断四边形EFGH的形状 并说明为什么.
例2 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线分别交BC和AD于点E和F,若平行四边形ABCD的面积为18,则图中阴影部分的面积是________.
五、能力训练
1.(绍兴中考)小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块玻璃,其编号应该是( )
A ①② B ①④ C ③④ D ②③
2.如图,在平行四边形ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
3.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF= BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长.
归纳与小结
作业
教材94页复习题.
复习目标
理解平行四边形的概念、掌握其性质和判定.
运用平行四边形的知识解决相关的证明问题和计算问题
知识点
1.平行四边形的定义
两组对边分别平行的四边形叫平行四边形.
2.平行四边形的性质
(1)两组对边分别平行,即AB∥CD, AD∥BC.
(2)两组对边分别相等,即AB=CD, AD=BC.
(3).两组对角分别相等,即∠ABC=∠ADC, ∠BAD=∠BCD;
(4)对角线互相平分,即OA=OC,OB=OD.
平行四边形是中心对称图形.
平行四边形的判定
分别平行的四边形是平行四边形.
两组对边
边 分别相等的四边形是平行四边形.
一组对边: 平行且相等的四边形是平行四边形.
对角线:对角线互相平分的四边形是平行四边形.
基础训练
1.已知:平行四边形ABCD中,∠A=100°,
则∠B= ________, ∠C=_________.
2.如图,在平行四边形ABCD中,AD=8cm,AB=6cm,DE平分∠ADC交BC于点E,则BE=______________.
3.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,若AC+BD=36,AB=10,则△AOB的周长为______________.
4.如图,四边形ABCD的对角线相交于点O,若AB//CD,请你添加一个条件____________,使得四边形ABCD为平行四边形.
典型例题
例1 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且E、F、G、H分别是OA、OB、OC、OD的中点.请判断四边形EFGH的形状 并说明为什么.
例2 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线分别交BC和AD于点E和F,若平行四边形ABCD的面积为18,则图中阴影部分的面积是________.
五、能力训练
1.(绍兴中考)小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块玻璃,其编号应该是( )
A ①② B ①④ C ③④ D ②③
2.如图,在平行四边形ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
3.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF= BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长.
归纳与小结
作业
教材94页复习题.
