华东师大版八年级下册数学 17.3.4 求一次函数的表达式(1)课件 (共16张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 17.3.4 求一次函数的表达式(1)课件 (共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 232.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 10:30:23 | ||
图片预览






文档简介
(共16张PPT)
求一次函数的表达式
17.3.4 求一次函数的表达式
1、能根据已知条件运用待定系数法确定一次函数的表达式。
2、通过函数图像和关系式,进一步加强数形结合的思想。
学习目标
自主学习
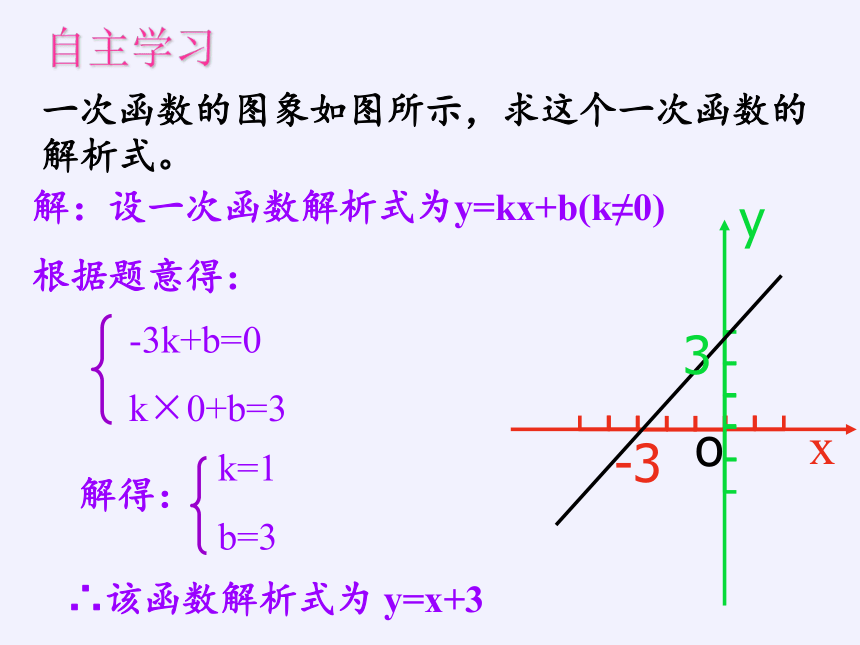
一次函数的图象如图所示,求这个一次函数的解析式。
x
y
o
-3
3
解:设一次函数解析式为y=kx+b(k≠0)
根据题意得:
解得:
k=1
b=3
∴该函数解析式为 y=x+3
-3k+b=0
k×0+b=3
所以该一次函数的表达式为__________.
把_______ , _______ 代入表达式得
__________
__________
设一次函数的表达式为_______________,
自主学习: 一次函数的图象经过点(0,2)和点(4,6),求出一次函数的表达式.
解:
y=kx+b(k≠0)
(0,2)
(4,6)
0×k+b=2
4k+b=6
2
1
y =x+2
解得:
k=____
b=____
用待定系数法解题一般分为几步?
一设、二列、三解、四代
1.设一次函数的一般形式y=kx+b(k≠0)
2.根据已知条件列出关于k , b的二元一次方程(组)
3.解这个方程(组),求出k , b
4 .将已经求出的 k, b的值代入解析式
待定系数法:
先设待求的函数关系式(其中含有待定的系数),再根据条件列出方程或方程组,求出待定系数,从而得到所求结果的方法,叫做待定系数法.
已知y与x成正比例,且当x=-1时,y=-6,求y与x之间的函数关系式。
练一练,我能行!
解:设所求函数关系式为 y=kx (k≠0)
根据题意得:-k=-6
∴ k=6
∴所求函数关系式为y=6x
已知y-2与x成正比例,当x=-2时,y=8,求y与x之间的函数关系式。
解:设所求函数关系式为 y-2=kx (k≠0)
根据题意得:-2k=8-2
∴k=-3 ∴ y-2=-3x
∴所求函数关系式为y=-3x+2
变式
总结
用待定系数法做题时,首先观察有几个待定系数(k,b)
如果待定系数只有一个(k或者b),那只需要一个点的坐标就可以了;
如果待定系数有两个(k、b都不知道),那就至少知道两个点的坐标才能做题。
利用函数性质求解析式(一)
将函数y=x+2的图象平移,使它经过点(1,-3),求平移后的直线所对应的函数解析式。
解:根据题意得:k=1
设所求直线的解析式为y=x+b
∴ -3 = 1 + b ∴b=-4
∴所求函数解析式为:y=x-4
已知一次函数的图象经过点(-1,-5),
且与y=3x+5的图象相交于y轴同一点, 求这个一次函数的解析式。
解:根据题意得:b=5
设所求直线的解析式为y=kx+5(k≠0)
∴ -k+5 =-5 ∴k=10
∴所求函数解析式为:y=10x+5
利用函数性质求解析式(二)
合作探究
已知直线L1:y =(2m+3)x +(4-n)和直线L2:y =(n-2)x + (4+m)平行,且与直线L3:y = 3x +(4+3m)交于y轴同一点,求m, n的值及直线L1的解析式。
2m+3=n-2
4-n=4+3m
解:根据题意得:
解得:
m=-1
n=3
∴所求函数解析式为:y=x+1
若直线y=kx+b平行于直线y=-3x+4,且
与直线y=2x-6交于y轴同一点,则此直线的函数
析式为 .
练一练,我能行!
y=-3x-6
1.若一次函数y=2x+b的图象经过点A(-1,1),则b= 该函数解析式为 .
3
y=2x+3
达标测评
2.如图,直线l是一次函数y=kx+b的图象,填空:
该函数解析式为_____________ .
2
1
3
-1
-2
-3
y
x
0
1
2
3
-1
-2
y=- x +2
3
2
第2题
3.若经过点(-2,3)的直线y=kx+b与直线y=3x-2平行,则该直线的函数解析式为 .
y=x+4
4.已知y-4与x的成正比例,且经过点(1,5),求y与x之间的函数关系式.
y=3x+9
一设、二列、三解、四代
注意:先看有几个待定系数,
然后确定要有几个点的坐标。
本节课你有什么收获?
用待定系数法解题一般分为几步?
待定系数法:
先设待求的函数关系式(其中含有未知的系数)再根据条件列出方程或方程组,求出未知系数,从而得到所求结果的方法,叫做待定系数法.
谢 谢
求一次函数的表达式
17.3.4 求一次函数的表达式
1、能根据已知条件运用待定系数法确定一次函数的表达式。
2、通过函数图像和关系式,进一步加强数形结合的思想。
学习目标
自主学习
一次函数的图象如图所示,求这个一次函数的解析式。
x
y
o
-3
3
解:设一次函数解析式为y=kx+b(k≠0)
根据题意得:
解得:
k=1
b=3
∴该函数解析式为 y=x+3
-3k+b=0
k×0+b=3
所以该一次函数的表达式为__________.
把_______ , _______ 代入表达式得
__________
__________
设一次函数的表达式为_______________,
自主学习: 一次函数的图象经过点(0,2)和点(4,6),求出一次函数的表达式.
解:
y=kx+b(k≠0)
(0,2)
(4,6)
0×k+b=2
4k+b=6
2
1
y =x+2
解得:
k=____
b=____
用待定系数法解题一般分为几步?
一设、二列、三解、四代
1.设一次函数的一般形式y=kx+b(k≠0)
2.根据已知条件列出关于k , b的二元一次方程(组)
3.解这个方程(组),求出k , b
4 .将已经求出的 k, b的值代入解析式
待定系数法:
先设待求的函数关系式(其中含有待定的系数),再根据条件列出方程或方程组,求出待定系数,从而得到所求结果的方法,叫做待定系数法.
已知y与x成正比例,且当x=-1时,y=-6,求y与x之间的函数关系式。
练一练,我能行!
解:设所求函数关系式为 y=kx (k≠0)
根据题意得:-k=-6
∴ k=6
∴所求函数关系式为y=6x
已知y-2与x成正比例,当x=-2时,y=8,求y与x之间的函数关系式。
解:设所求函数关系式为 y-2=kx (k≠0)
根据题意得:-2k=8-2
∴k=-3 ∴ y-2=-3x
∴所求函数关系式为y=-3x+2
变式
总结
用待定系数法做题时,首先观察有几个待定系数(k,b)
如果待定系数只有一个(k或者b),那只需要一个点的坐标就可以了;
如果待定系数有两个(k、b都不知道),那就至少知道两个点的坐标才能做题。
利用函数性质求解析式(一)
将函数y=x+2的图象平移,使它经过点(1,-3),求平移后的直线所对应的函数解析式。
解:根据题意得:k=1
设所求直线的解析式为y=x+b
∴ -3 = 1 + b ∴b=-4
∴所求函数解析式为:y=x-4
已知一次函数的图象经过点(-1,-5),
且与y=3x+5的图象相交于y轴同一点, 求这个一次函数的解析式。
解:根据题意得:b=5
设所求直线的解析式为y=kx+5(k≠0)
∴ -k+5 =-5 ∴k=10
∴所求函数解析式为:y=10x+5
利用函数性质求解析式(二)
合作探究
已知直线L1:y =(2m+3)x +(4-n)和直线L2:y =(n-2)x + (4+m)平行,且与直线L3:y = 3x +(4+3m)交于y轴同一点,求m, n的值及直线L1的解析式。
2m+3=n-2
4-n=4+3m
解:根据题意得:
解得:
m=-1
n=3
∴所求函数解析式为:y=x+1
若直线y=kx+b平行于直线y=-3x+4,且
与直线y=2x-6交于y轴同一点,则此直线的函数
析式为 .
练一练,我能行!
y=-3x-6
1.若一次函数y=2x+b的图象经过点A(-1,1),则b= 该函数解析式为 .
3
y=2x+3
达标测评
2.如图,直线l是一次函数y=kx+b的图象,填空:
该函数解析式为_____________ .
2
1
3
-1
-2
-3
y
x
0
1
2
3
-1
-2
y=- x +2
3
2
第2题
3.若经过点(-2,3)的直线y=kx+b与直线y=3x-2平行,则该直线的函数解析式为 .
y=x+4
4.已知y-4与x的成正比例,且经过点(1,5),求y与x之间的函数关系式.
y=3x+9
一设、二列、三解、四代
注意:先看有几个待定系数,
然后确定要有几个点的坐标。
本节课你有什么收获?
用待定系数法解题一般分为几步?
待定系数法:
先设待求的函数关系式(其中含有未知的系数)再根据条件列出方程或方程组,求出未知系数,从而得到所求结果的方法,叫做待定系数法.
谢 谢
