华东师大版八年级下册数学19.1.1 矩形的性质课件 (共14张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学19.1.1 矩形的性质课件 (共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 406.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 10:32:51 | ||
图片预览




文档简介
(共14张PPT)
矩形的性质
华东师大版八年级下册第十九章
学习目标
1.将了解掌握矩形的定义和性质.
2.经历矩形性质的探究过程.
3.将学会运用矩形的性质解决有关问题.
视频助学请先思考引导问题,再看视频【矩形的性质】.......
引导问题 1 矩形的定义是什么?
引导问题 2 矩形的性质有哪些?如何证明?
引导问题 3 如何运用矩形的定义和性质解决有关问题?
矩形的定义是:有一个角是直角的平行四边形是矩形。
复习回顾
平行四边形有哪些性质?
(从边、角、对角线、对称性四个方面研究)
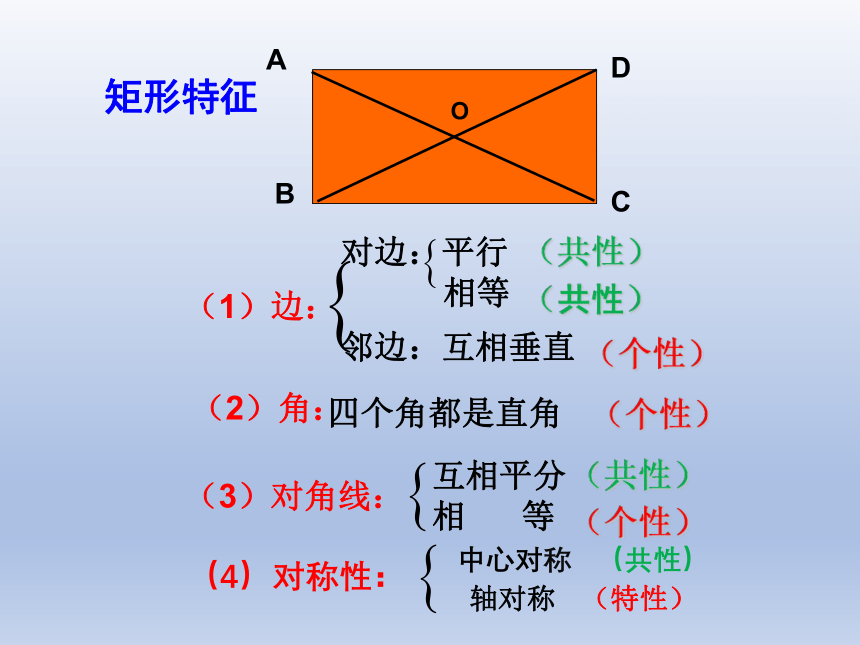
邻边:互相垂直
四个角都是直角
互相平分
相 等
(1)边:
(2)角:
(3)对角线:
A
B
C
D
对边:平行
相等
(共性)
(共性)
(个性)
(个性)
(个性)
(共性)
O
矩形特征
(4)对称性:
中心对称 (共性)
轴对称 (特性)
A
B
C
D
O
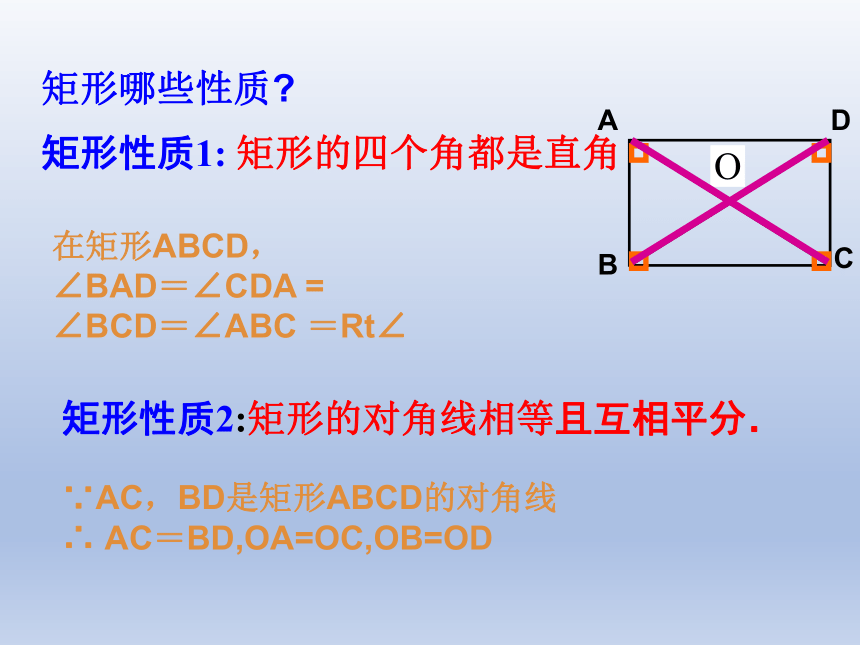
矩形哪些性质
矩形性质1: 矩形的四个角都是直角
在矩形ABCD,
∠BAD=∠CDA =
∠BCD=∠ABC =Rt∠
矩形性质2:矩形的对角线相等且互相平分.
∵AC,BD是矩形ABCD的对角线
∴ AC=BD,OA=OC,OB=OD
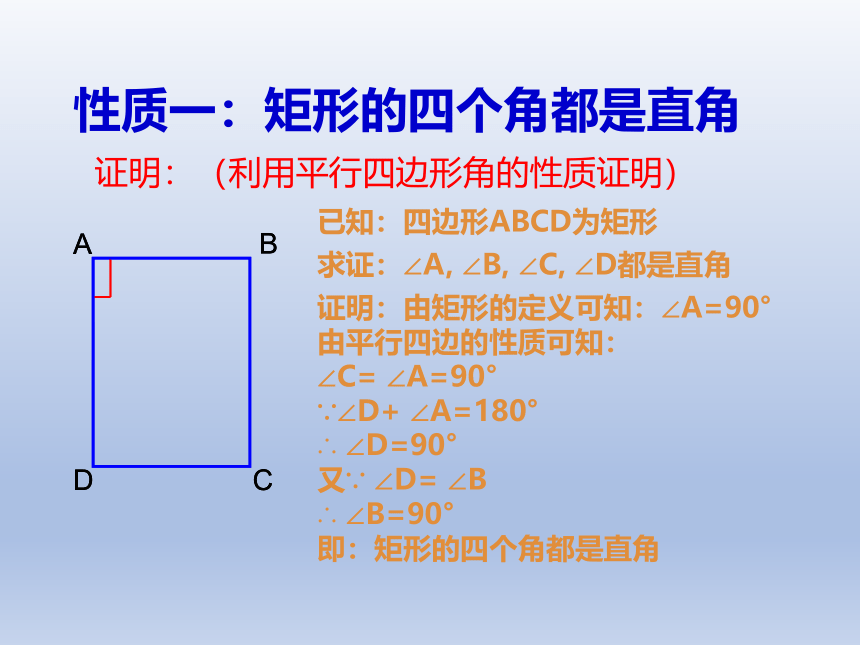
性质一:矩形的四个角都是直角
证明:(利用平行四边形角的性质证明)
证明:由矩形的定义可知:∠A=90°
由平行四边的性质可知:
∠C= ∠A=90°
∵∠D+ ∠A=180°
∴ ∠D=90°
又∵ ∠D= ∠B
∴ ∠B=90°
即:矩形的四个角都是直角
A
D
C
B
已知:四边形ABCD为矩形
求证:∠A, ∠B, ∠C, ∠D都是直角
A
D
C
B
性质二:矩形的对角线相等
O
证明:∵ABCD为矩形
∴AD=CB AB=CD
∠ADC=∠CBA
在△ACD和△CAB中
AD=CB ∠ADC=∠CBA AB=CD
∴ △ACD≌ △CAB
则: AC=BD
即:矩形的对角线相等
已知:四边形ABCD为矩形
求证:AC=BD
A
D
C
B
(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度 (B)对角相等
(C)对边平行且相等 (D)对角线相等
(2)下面性质中,矩形不一定具有的是( )
(A)对角线相等 (B)四个角相等
(C)是轴对称图形 (D)对角线垂直
(3) 已知矩形的一条对角线与一边的夹角是40°,
则两条对角线所夹锐角的度数为 ( )
(A)50° (B)60° (C)70° (D)80°
D
第一关
D
D
性质应用
(第1题图)
2、如图,在矩形ABCD中,矩形ABCD的对角线AC、BD相交于点O,AC=4cm,∠AOB=60°,则AB= cm.
(第2题图)
2
方法:如果矩形两对角线的夹角是60°或120°, 则其中必有等边三角形。
1.在矩形ABCD中,AE⊥BD于E,
若BE=OE=1,则
AC= , AB= ,
4
2
B
C
E
A
O
D
性质应用
3、如图,在矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长和是86cm,矩形的对角线长是13cm,那么该矩形的周长是多少cm
解: ∵ △AOB、 △BOC、 △COD和△AOD四个三角形的周长和为86cm,
又∵AC=BD=13cm,
∴ AB+BC+CD+DA=86-2(AC+BD)=86-4×13=34(cm)
即矩形ABCD的周长等于34cm。
方法:矩形问题可以转化成等边三角形或直角三角形的问题去解决。
1.如图,矩形ABCD的两条对角线交于点O,且
∠AOD=120°,你能说明AC=2AB吗?
解:∵四边形ABCD是矩形
∴AC = BD( )
∴ OA= OC = AC
OB= OD = BD( )
矩形的对角线相等
∴ OA= OB
∴ △AOB 是等边三角形∴OA=OB=AB
∴AC = 2OA=2AB.
平行四边形的对角线互相平分
∵∠AOD=120°
∴∠AOB=180°-∠AOD = 60°
练一练
邻边:互相垂直
四个角都是直角
互相平分
相 等
(1)边:
(2)角:
(3)对角线:
对边: 平行
相等
(共性)
(共性)
(特性)
(特性)
(特性)
(共性)
课堂小结
这节课,你学到了什么?
知识:
(4)对称性:
中心对称 (共性)
轴对称(特性)
课堂小结
这节课,你学到了什么?
1、如果矩形两对角线的夹角是60°或120°, 则其中必有等边三角形。
2、矩形问题可以转化成等边三角形或直角三角形的问题去解决。
方法:
矩形的性质
华东师大版八年级下册第十九章
学习目标
1.将了解掌握矩形的定义和性质.
2.经历矩形性质的探究过程.
3.将学会运用矩形的性质解决有关问题.
视频助学请先思考引导问题,再看视频【矩形的性质】.......
引导问题 1 矩形的定义是什么?
引导问题 2 矩形的性质有哪些?如何证明?
引导问题 3 如何运用矩形的定义和性质解决有关问题?
矩形的定义是:有一个角是直角的平行四边形是矩形。
复习回顾
平行四边形有哪些性质?
(从边、角、对角线、对称性四个方面研究)
邻边:互相垂直
四个角都是直角
互相平分
相 等
(1)边:
(2)角:
(3)对角线:
A
B
C
D
对边:平行
相等
(共性)
(共性)
(个性)
(个性)
(个性)
(共性)
O
矩形特征
(4)对称性:
中心对称 (共性)
轴对称 (特性)
A
B
C
D
O
矩形哪些性质
矩形性质1: 矩形的四个角都是直角
在矩形ABCD,
∠BAD=∠CDA =
∠BCD=∠ABC =Rt∠
矩形性质2:矩形的对角线相等且互相平分.
∵AC,BD是矩形ABCD的对角线
∴ AC=BD,OA=OC,OB=OD
性质一:矩形的四个角都是直角
证明:(利用平行四边形角的性质证明)
证明:由矩形的定义可知:∠A=90°
由平行四边的性质可知:
∠C= ∠A=90°
∵∠D+ ∠A=180°
∴ ∠D=90°
又∵ ∠D= ∠B
∴ ∠B=90°
即:矩形的四个角都是直角
A
D
C
B
已知:四边形ABCD为矩形
求证:∠A, ∠B, ∠C, ∠D都是直角
A
D
C
B
性质二:矩形的对角线相等
O
证明:∵ABCD为矩形
∴AD=CB AB=CD
∠ADC=∠CBA
在△ACD和△CAB中
AD=CB ∠ADC=∠CBA AB=CD
∴ △ACD≌ △CAB
则: AC=BD
即:矩形的对角线相等
已知:四边形ABCD为矩形
求证:AC=BD
A
D
C
B
(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度 (B)对角相等
(C)对边平行且相等 (D)对角线相等
(2)下面性质中,矩形不一定具有的是( )
(A)对角线相等 (B)四个角相等
(C)是轴对称图形 (D)对角线垂直
(3) 已知矩形的一条对角线与一边的夹角是40°,
则两条对角线所夹锐角的度数为 ( )
(A)50° (B)60° (C)70° (D)80°
D
第一关
D
D
性质应用
(第1题图)
2、如图,在矩形ABCD中,矩形ABCD的对角线AC、BD相交于点O,AC=4cm,∠AOB=60°,则AB= cm.
(第2题图)
2
方法:如果矩形两对角线的夹角是60°或120°, 则其中必有等边三角形。
1.在矩形ABCD中,AE⊥BD于E,
若BE=OE=1,则
AC= , AB= ,
4
2
B
C
E
A
O
D
性质应用
3、如图,在矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长和是86cm,矩形的对角线长是13cm,那么该矩形的周长是多少cm
解: ∵ △AOB、 △BOC、 △COD和△AOD四个三角形的周长和为86cm,
又∵AC=BD=13cm,
∴ AB+BC+CD+DA=86-2(AC+BD)=86-4×13=34(cm)
即矩形ABCD的周长等于34cm。
方法:矩形问题可以转化成等边三角形或直角三角形的问题去解决。
1.如图,矩形ABCD的两条对角线交于点O,且
∠AOD=120°,你能说明AC=2AB吗?
解:∵四边形ABCD是矩形
∴AC = BD( )
∴ OA= OC = AC
OB= OD = BD( )
矩形的对角线相等
∴ OA= OB
∴ △AOB 是等边三角形∴OA=OB=AB
∴AC = 2OA=2AB.
平行四边形的对角线互相平分
∵∠AOD=120°
∴∠AOB=180°-∠AOD = 60°
练一练
邻边:互相垂直
四个角都是直角
互相平分
相 等
(1)边:
(2)角:
(3)对角线:
对边: 平行
相等
(共性)
(共性)
(特性)
(特性)
(特性)
(共性)
课堂小结
这节课,你学到了什么?
知识:
(4)对称性:
中心对称 (共性)
轴对称(特性)
课堂小结
这节课,你学到了什么?
1、如果矩形两对角线的夹角是60°或120°, 则其中必有等边三角形。
2、矩形问题可以转化成等边三角形或直角三角形的问题去解决。
方法:
