华东师大版八年级下册数学19.1.2 矩形的判定(11)课件 (共14张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学19.1.2 矩形的判定(11)课件 (共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 664.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 10:35:21 | ||
图片预览





文档简介
(共14张PPT)
矩形的判定
18.2.1 特殊的平行四边形
马安中学 王波
学习目标:
1、能应用矩形的定义、判定定理,解决简单的证明题和计算题,进一步培养分析能力;
2、培养综合应用知识、分析解决问题的能力。
矩形
☆定义:
☆性质:
有一个角是直角的平行四边形是矩形。
边
角
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且平分;
对角线
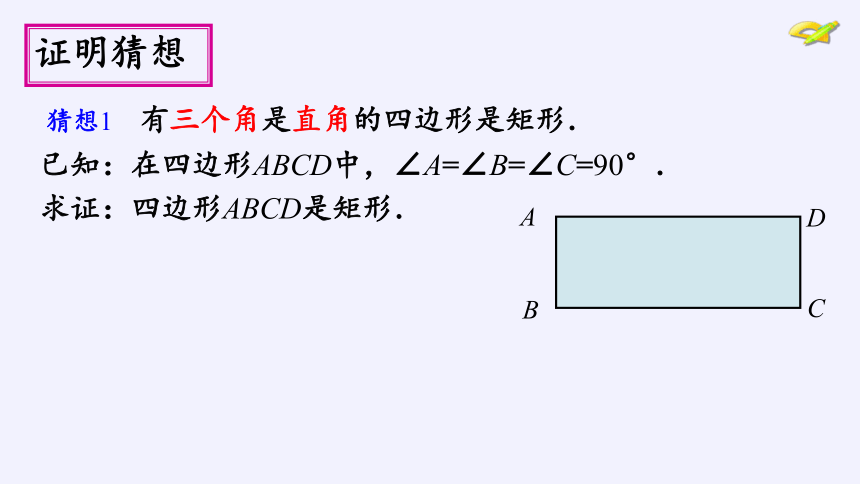
证明猜想
猜想1 有三个角是直角的四边形是矩形.
已知:在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
B
C
D
A
有三个角是直角的四边形是矩形
A
B
C
D
已知:在四边形ABCD中,
∠A= ∠B= ∠C=90°
求证:四边形ABCD是矩形
证明:∵ ∠A= ∠B= ∠C=90°
∴ ∠A + ∠B = 180°
∠B + ∠C = 180°
∴AD∥BC, AB∥DC
∴四边形ABCD是平行四边形
∵ ∠A=90°
∴四边形ABCD是矩形
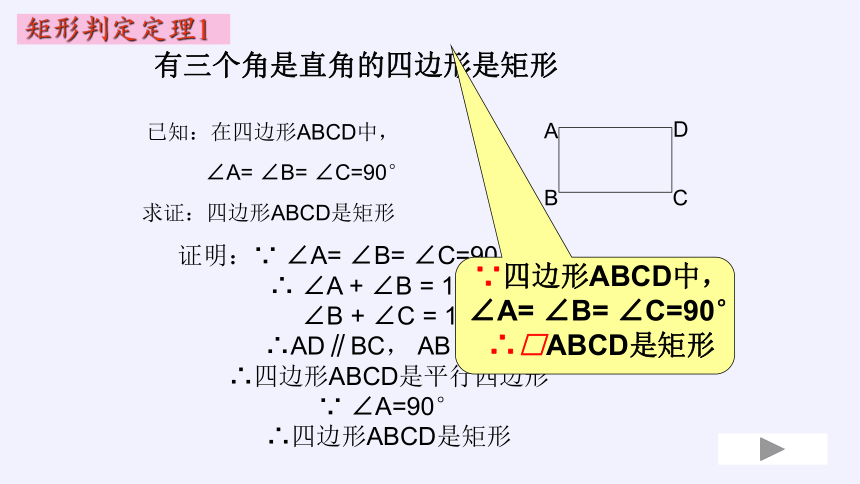
矩形判定定理1
∵四边形ABCD中,
∠A= ∠B= ∠C=90°
∴□ABCD是矩形
证明猜想
猜想2 对角线相等的平行四边形是矩形.
B
C
D
A
o
已知:在平行四边形ABCD中,AC=BD
求证:四边形ABCD是矩形
对角线相等的平行四边形是矩形。
已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。
A
B
C
D
证明:
∵平行四边形ABCD ∴AB=CD
∵BC=BC
AC=BD
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形
∴四边形ABCD是矩形
∴ ∠ABC=∠DCB
判定定理2
∵□ABCD,AC=BD
∴□ABCD是矩形
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形 。
有三个角是直角的四边形是矩形 。
方法1:
方法2:
方法3:
辩一辩
判断下列说法对错?为什么?
(1)有一个角是直角的四边形是矩形;
(2)有四个角是直角的四边形是矩形;
(3)四个角都相等的四边形是矩形;
(4)对角线相等的四边形是矩形;
(5)对角线相等且互相垂直的四边形是矩形;
(6)对角线互相平分且相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(8)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(9)两组对边分别平行,且对角线相等的四边形是矩形。
A
B
C
D
O
用一用
已知:在平行四边形ABCD中,对角线AC,BD相交于
点 O,且∠1=∠2 ;
求证:四边形ABCD是矩形
1
2
说说本节课的收获和困惑!
课后作业:
1、导学案相应练习;
2、教材55页练习1、练习2.
谢 谢
矩形的判定
18.2.1 特殊的平行四边形
马安中学 王波
学习目标:
1、能应用矩形的定义、判定定理,解决简单的证明题和计算题,进一步培养分析能力;
2、培养综合应用知识、分析解决问题的能力。
矩形
☆定义:
☆性质:
有一个角是直角的平行四边形是矩形。
边
角
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且平分;
对角线
证明猜想
猜想1 有三个角是直角的四边形是矩形.
已知:在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
B
C
D
A
有三个角是直角的四边形是矩形
A
B
C
D
已知:在四边形ABCD中,
∠A= ∠B= ∠C=90°
求证:四边形ABCD是矩形
证明:∵ ∠A= ∠B= ∠C=90°
∴ ∠A + ∠B = 180°
∠B + ∠C = 180°
∴AD∥BC, AB∥DC
∴四边形ABCD是平行四边形
∵ ∠A=90°
∴四边形ABCD是矩形
矩形判定定理1
∵四边形ABCD中,
∠A= ∠B= ∠C=90°
∴□ABCD是矩形
证明猜想
猜想2 对角线相等的平行四边形是矩形.
B
C
D
A
o
已知:在平行四边形ABCD中,AC=BD
求证:四边形ABCD是矩形
对角线相等的平行四边形是矩形。
已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。
A
B
C
D
证明:
∵平行四边形ABCD ∴AB=CD
∵BC=BC
AC=BD
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形
∴四边形ABCD是矩形
∴ ∠ABC=∠DCB
判定定理2
∵□ABCD,AC=BD
∴□ABCD是矩形
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形 。
有三个角是直角的四边形是矩形 。
方法1:
方法2:
方法3:
辩一辩
判断下列说法对错?为什么?
(1)有一个角是直角的四边形是矩形;
(2)有四个角是直角的四边形是矩形;
(3)四个角都相等的四边形是矩形;
(4)对角线相等的四边形是矩形;
(5)对角线相等且互相垂直的四边形是矩形;
(6)对角线互相平分且相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(8)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(9)两组对边分别平行,且对角线相等的四边形是矩形。
A
B
C
D
O
用一用
已知:在平行四边形ABCD中,对角线AC,BD相交于
点 O,且∠1=∠2 ;
求证:四边形ABCD是矩形
1
2
说说本节课的收获和困惑!
课后作业:
1、导学案相应练习;
2、教材55页练习1、练习2.
谢 谢
