人教版九年级下册数学 26.1反比例函数 同步练习(word,含答案)
文档属性
| 名称 | 人教版九年级下册数学 26.1反比例函数 同步练习(word,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 135.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-13 10:41:27 | ||
图片预览



文档简介
26.1反比例函数 同步练习
一.选择题
1.下列函数中,y是x的反比例函数的是( )
A.y= B.y= C.y= D.y=+2
2.下列各点在函数y=﹣的图象上的是( )
A.(2,1) B.(﹣2,0) C.(2,0) D.(﹣2,1)
3.函数y=kx+k与y=(k≠0)在同一平面直角坐标系的图象可能是( )
A. B.
C. D.
4.已知点A(x,y)是反比例函数y=图象上的一点,若x>3,则y的取值范围是( )
A.2<y<6 B.0<y<2 C.y<2 D.y>2
5.如图,点A在函数y=﹣图象上,过点A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )
A.2 B.4 C.8 D.16
6.关于反比例函数,下列说法错误的是( )
A.图象经过点(1,﹣3) B.y随x的增大而增大
C.图象关于原点对称 D.图象与坐标轴没有交点
二.填空题
7.给出的六个关系式:①x(y+1);②y=;③y=;④y=﹣;⑤y=;⑥y=x﹣1,其中y是x的反比例函数是 .
8.反比例函数y=经过二、四象限,则k .
9.已知点A1(﹣1,y1),A2(﹣3,y2)都在反比例函数y=(k>0)的图象上,则y1与y2的大小关系为 .
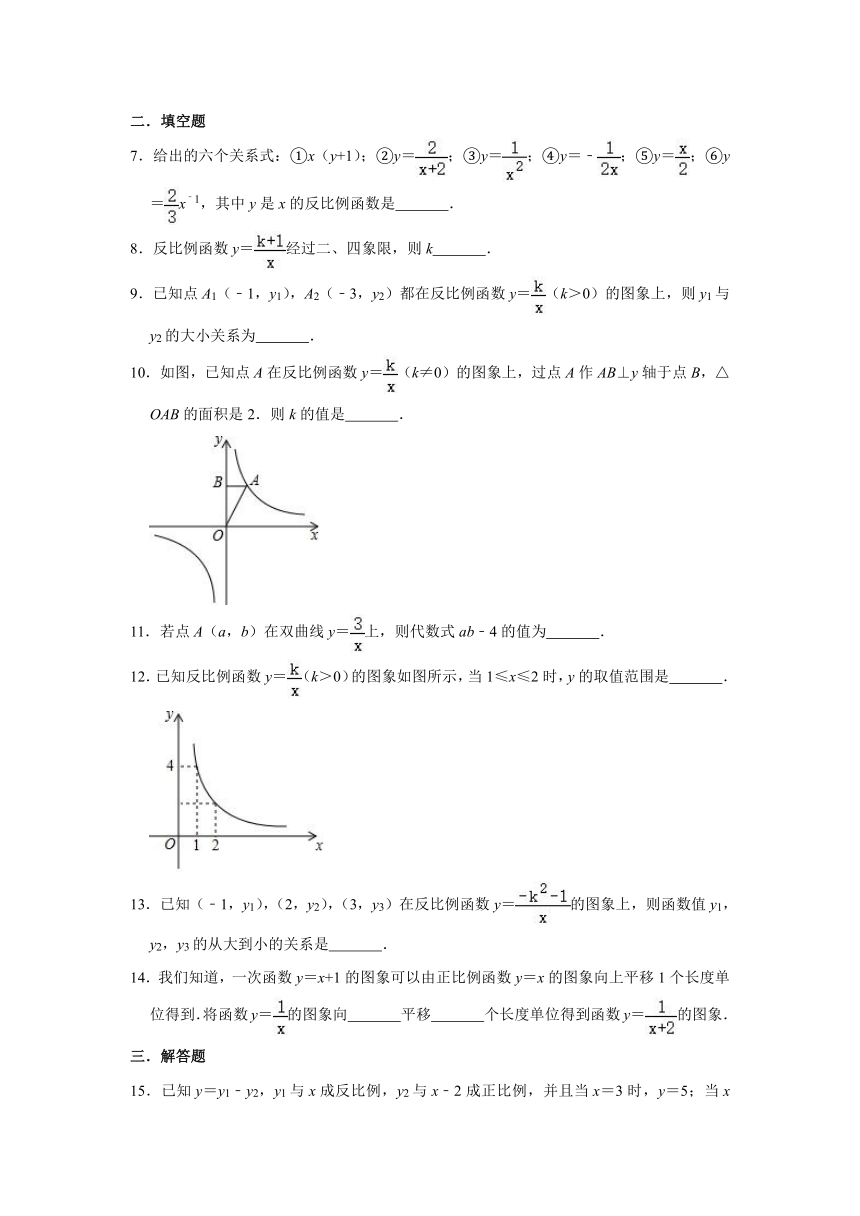
10.如图,已知点A在反比例函数y=(k≠0)的图象上,过点A作AB⊥y轴于点B,△OAB的面积是2.则k的值是 .
11.若点A(a,b)在双曲线y=上,则代数式ab﹣4的值为 .
12.已知反比例函数y=(k>0)的图象如图所示,当1≤x≤2时,y的取值范围是 .
13.已知(﹣1,y1),(2,y2),(3,y3)在反比例函数y=的图象上,则函数值y1,y2,y3的从大到小的关系是 .
14.我们知道,一次函数y=x+1的图象可以由正比例函数y=x的图象向上平移1个长度单位得到.将函数y=的图象向 平移 个长度单位得到函数y=的图象.
三.解答题
15.已知y=y1﹣y2,y1与x成反比例,y2与x﹣2成正比例,并且当x=3时,y=5;当x=1时,y=﹣1.
(1)y与x的函数表达式;
(2)当x=﹣1时,求y的值.
16.函数y=x的图象与函数y=的图象相交于点P(2,m).
(1)求m,k的值;
(2)将函数y=x的图象向左平移4个单位,求与函数y=的交点坐标.
17.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于A,B两点,与x轴交于点P,过点A作AE⊥x轴于点E,AE=3.
(1)求点A的坐标;
(2)若PA:PB=3:1,求一次函数的解析式.
18.如图,一次函数y=kx+b的图象交反比例函数y=的图象于A(2,﹣4),B(a,﹣1)两点.
(1)求反比例函数与一次函数解析式.
(2)连接OA,OB,求△OAB的面积.
(3)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?
参考答案
一.选择题
1.解:A、该函数是正比例函数,故本选项不符合题意;
B、该函数是反比例函数,故本选项符合题意;
C、该函数是y与(x+2)成反比例函数关系,故本选项不符合题意;
D、该函数不符合反比例函数的定义,故本选项不符合题意.
故选:B.
2.解:∵函数解析式为y=﹣,
把四个选项的坐标依次代入函数解析式,仅选项D的坐标(﹣2,1)在函数y=﹣的图象上,
∴D选项符合题意,A、B、C选项不符合题意,
故选:D.
3.解:①当k>0时,y=kx+k过一、二、三象限;y=(k≠0)过一、三象限;
②当k<0时,y=kx+k过二、三、四象象限;y=(k≠0)过二、四象限.
观察图形可知,只有B选项符合题意.
故选:B.
4.解:∵y=,
∴在第一象限内,y随x的增大而减小,
∴当x>3时,0<y<2,
故选:B.
5.解:∵点A在函数y=﹣图象上,过点A作AB⊥x轴于点B,连接OA,
∴S△ABO=|k|=×|﹣8|=4.
故选:B.
6.解:A、反比例函数,当x=1时y=﹣3,说法正确,故本选项不符合题意;
B、反比例函数中k=﹣3<0,则该函数图象经过第二、四象限,需要强调在每个象限象限内y随x的增大而增大,故说法错误,本选项符合题意;
C、反比例函数的图象关于原点对称,说法正确,故本选项不符合题意;
D、图象与坐标轴没有交点,说法正确,故本选项不符合题意.
故选:B.
二.填空题
7.解:①x(y+1)不是函数,不符合题意;
②y=是y关于x+2的反比例函数,不符合题意;
③y=是y关于x2的反比例函数,不符合题意;
④y=﹣=,是y关于x的反比例函数,符合题意;
⑤y=是y关于x的正比例函数,不符合题意;
⑥y=x﹣1=,是y关于x的反比例函数,符合题意;
故答案为:④⑥.
8.解:∵反比例函数y=经过二、四象限,
∴k+1<0,
∴k<﹣1,
故答案为:<﹣1.
9.解:∵y=(k>0),
∴此函数在每个象限内,y随x的增大而减小,
∵点A1(﹣1,y1),A2(﹣3,y2)都在反比例函数y=(k>0)的图象上,﹣1>﹣3,
∴y1<y2,
故答案为y1<y2.
10.解:设点A的坐标为(xA,yA),AB⊥y轴,
由题意可知:,
∴yA xA=4,
又点A在反比例函数图象上,
故有k=xA yA=4.
故答案为:4.
11.解:∵点A(a,b)在双曲线y=上,
∴3=ab,
∴ab﹣4=3﹣4=﹣1.
故答案为:﹣1.
12.解:由图象知,当1≤x≤2时,y的取值范围是2≤y≤4,
故答案为:2≤y≤4.
13.解:∵﹣k2﹣1<0,
∴反比例函数图象分布在第二、四象限,在每一象限y随x的增大而增大,
∴y1>0,y2<y3<0,
∴y2<y3<y1.
故答案为y1>y3>y2.
14.解:函数y=的图象可以看成是由反比例函数y=的图象向左平移2个单位长度得到.
故答案为:左,2.
三.解答题
15.解:(1)设y1=,y2=b(x﹣2),则y=﹣b(x﹣2),
根据题意得,解得,
所以y关于x的函数关系式为y=+4(x﹣2);
(2)把x=﹣1代入y=+4(x﹣2);
得y=﹣3+4×(﹣1﹣2)=﹣15.
16.解:(1)把x=2代入y=x,得m=2,
把(2,2)代入,得k=4
∴m=2,k=4;
(2)将函数y=x的图象向左平移4个单位后函数解析式为:y=x+4,
联立方程组,
解得,,
∴交点坐标为(﹣2+2,2+2)和(﹣2﹣2,2﹣2).
17.解:(1)当y=3时,3=,解得x=2,
∴点A的坐标为(2,3);
(2)作BF⊥x轴于F,如图,
∵AE∥BF,
∴==3,
∴BF=1,
当y=﹣1时,﹣1=,解得x=﹣6,
∴B(﹣6,﹣1),
把A(2,3),B(﹣6,﹣1)代入y=kx+b,解得,
∴一次函数解析式为y=x+2.
18.解:(1)把A(2,﹣4)的坐标代入y=得:m=﹣8,
∴反比例函数的解析式是y=﹣;
把B(a,﹣1)的坐标代入y=﹣得:﹣1=﹣,
解得:a=8,
∴B点坐标为(8,﹣1),
把A(2,﹣4)、B(8,﹣1)的坐标代入y=kx+b,得:,
解得:,
∴一次函数解析式为y=x﹣5;
(2)∵y=x﹣5,
∴当y=0时,x=10,
∴OC=10,
∴△AOB的面积=△AOC的面积﹣三角形BOC的面积
=×10×4﹣×10×1
=15;
(3)由图象知,当0<x<2或x>8时,一次函数的值大于反比例函数的值.
一.选择题
1.下列函数中,y是x的反比例函数的是( )
A.y= B.y= C.y= D.y=+2
2.下列各点在函数y=﹣的图象上的是( )
A.(2,1) B.(﹣2,0) C.(2,0) D.(﹣2,1)
3.函数y=kx+k与y=(k≠0)在同一平面直角坐标系的图象可能是( )
A. B.
C. D.
4.已知点A(x,y)是反比例函数y=图象上的一点,若x>3,则y的取值范围是( )
A.2<y<6 B.0<y<2 C.y<2 D.y>2
5.如图,点A在函数y=﹣图象上,过点A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )
A.2 B.4 C.8 D.16
6.关于反比例函数,下列说法错误的是( )
A.图象经过点(1,﹣3) B.y随x的增大而增大
C.图象关于原点对称 D.图象与坐标轴没有交点
二.填空题
7.给出的六个关系式:①x(y+1);②y=;③y=;④y=﹣;⑤y=;⑥y=x﹣1,其中y是x的反比例函数是 .
8.反比例函数y=经过二、四象限,则k .
9.已知点A1(﹣1,y1),A2(﹣3,y2)都在反比例函数y=(k>0)的图象上,则y1与y2的大小关系为 .
10.如图,已知点A在反比例函数y=(k≠0)的图象上,过点A作AB⊥y轴于点B,△OAB的面积是2.则k的值是 .
11.若点A(a,b)在双曲线y=上,则代数式ab﹣4的值为 .
12.已知反比例函数y=(k>0)的图象如图所示,当1≤x≤2时,y的取值范围是 .
13.已知(﹣1,y1),(2,y2),(3,y3)在反比例函数y=的图象上,则函数值y1,y2,y3的从大到小的关系是 .
14.我们知道,一次函数y=x+1的图象可以由正比例函数y=x的图象向上平移1个长度单位得到.将函数y=的图象向 平移 个长度单位得到函数y=的图象.
三.解答题
15.已知y=y1﹣y2,y1与x成反比例,y2与x﹣2成正比例,并且当x=3时,y=5;当x=1时,y=﹣1.
(1)y与x的函数表达式;
(2)当x=﹣1时,求y的值.
16.函数y=x的图象与函数y=的图象相交于点P(2,m).
(1)求m,k的值;
(2)将函数y=x的图象向左平移4个单位,求与函数y=的交点坐标.
17.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于A,B两点,与x轴交于点P,过点A作AE⊥x轴于点E,AE=3.
(1)求点A的坐标;
(2)若PA:PB=3:1,求一次函数的解析式.
18.如图,一次函数y=kx+b的图象交反比例函数y=的图象于A(2,﹣4),B(a,﹣1)两点.
(1)求反比例函数与一次函数解析式.
(2)连接OA,OB,求△OAB的面积.
(3)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?
参考答案
一.选择题
1.解:A、该函数是正比例函数,故本选项不符合题意;
B、该函数是反比例函数,故本选项符合题意;
C、该函数是y与(x+2)成反比例函数关系,故本选项不符合题意;
D、该函数不符合反比例函数的定义,故本选项不符合题意.
故选:B.
2.解:∵函数解析式为y=﹣,
把四个选项的坐标依次代入函数解析式,仅选项D的坐标(﹣2,1)在函数y=﹣的图象上,
∴D选项符合题意,A、B、C选项不符合题意,
故选:D.
3.解:①当k>0时,y=kx+k过一、二、三象限;y=(k≠0)过一、三象限;
②当k<0时,y=kx+k过二、三、四象象限;y=(k≠0)过二、四象限.
观察图形可知,只有B选项符合题意.
故选:B.
4.解:∵y=,
∴在第一象限内,y随x的增大而减小,
∴当x>3时,0<y<2,
故选:B.
5.解:∵点A在函数y=﹣图象上,过点A作AB⊥x轴于点B,连接OA,
∴S△ABO=|k|=×|﹣8|=4.
故选:B.
6.解:A、反比例函数,当x=1时y=﹣3,说法正确,故本选项不符合题意;
B、反比例函数中k=﹣3<0,则该函数图象经过第二、四象限,需要强调在每个象限象限内y随x的增大而增大,故说法错误,本选项符合题意;
C、反比例函数的图象关于原点对称,说法正确,故本选项不符合题意;
D、图象与坐标轴没有交点,说法正确,故本选项不符合题意.
故选:B.
二.填空题
7.解:①x(y+1)不是函数,不符合题意;
②y=是y关于x+2的反比例函数,不符合题意;
③y=是y关于x2的反比例函数,不符合题意;
④y=﹣=,是y关于x的反比例函数,符合题意;
⑤y=是y关于x的正比例函数,不符合题意;
⑥y=x﹣1=,是y关于x的反比例函数,符合题意;
故答案为:④⑥.
8.解:∵反比例函数y=经过二、四象限,
∴k+1<0,
∴k<﹣1,
故答案为:<﹣1.
9.解:∵y=(k>0),
∴此函数在每个象限内,y随x的增大而减小,
∵点A1(﹣1,y1),A2(﹣3,y2)都在反比例函数y=(k>0)的图象上,﹣1>﹣3,
∴y1<y2,
故答案为y1<y2.
10.解:设点A的坐标为(xA,yA),AB⊥y轴,
由题意可知:,
∴yA xA=4,
又点A在反比例函数图象上,
故有k=xA yA=4.
故答案为:4.
11.解:∵点A(a,b)在双曲线y=上,
∴3=ab,
∴ab﹣4=3﹣4=﹣1.
故答案为:﹣1.
12.解:由图象知,当1≤x≤2时,y的取值范围是2≤y≤4,
故答案为:2≤y≤4.
13.解:∵﹣k2﹣1<0,
∴反比例函数图象分布在第二、四象限,在每一象限y随x的增大而增大,
∴y1>0,y2<y3<0,
∴y2<y3<y1.
故答案为y1>y3>y2.
14.解:函数y=的图象可以看成是由反比例函数y=的图象向左平移2个单位长度得到.
故答案为:左,2.
三.解答题
15.解:(1)设y1=,y2=b(x﹣2),则y=﹣b(x﹣2),
根据题意得,解得,
所以y关于x的函数关系式为y=+4(x﹣2);
(2)把x=﹣1代入y=+4(x﹣2);
得y=﹣3+4×(﹣1﹣2)=﹣15.
16.解:(1)把x=2代入y=x,得m=2,
把(2,2)代入,得k=4
∴m=2,k=4;
(2)将函数y=x的图象向左平移4个单位后函数解析式为:y=x+4,
联立方程组,
解得,,
∴交点坐标为(﹣2+2,2+2)和(﹣2﹣2,2﹣2).
17.解:(1)当y=3时,3=,解得x=2,
∴点A的坐标为(2,3);
(2)作BF⊥x轴于F,如图,
∵AE∥BF,
∴==3,
∴BF=1,
当y=﹣1时,﹣1=,解得x=﹣6,
∴B(﹣6,﹣1),
把A(2,3),B(﹣6,﹣1)代入y=kx+b,解得,
∴一次函数解析式为y=x+2.
18.解:(1)把A(2,﹣4)的坐标代入y=得:m=﹣8,
∴反比例函数的解析式是y=﹣;
把B(a,﹣1)的坐标代入y=﹣得:﹣1=﹣,
解得:a=8,
∴B点坐标为(8,﹣1),
把A(2,﹣4)、B(8,﹣1)的坐标代入y=kx+b,得:,
解得:,
∴一次函数解析式为y=x﹣5;
(2)∵y=x﹣5,
∴当y=0时,x=10,
∴OC=10,
∴△AOB的面积=△AOC的面积﹣三角形BOC的面积
=×10×4﹣×10×1
=15;
(3)由图象知,当0<x<2或x>8时,一次函数的值大于反比例函数的值.
