鲁教版数学七年级下册 第七章 二元一次方程组 达标测试卷(含答案)
文档属性
| 名称 | 鲁教版数学七年级下册 第七章 二元一次方程组 达标测试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 17:51:19 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第七章 二元一次方程组达标测试卷
一、选择题(每小题3分,共30分)
1.下列不是二元一次方程组的是( )
A. B. C. D.
2.用加减法解方程组时,下列解法错误的是( )
A.①×3-②×2,消去x B.①×2-②×3,消去y
C.①×(-3)+②×2,消去x D.①×2-②×(-3),消去y
3.已知关于m,n的二元一次方程5m-2n=-3,当m与n相等时,m与n的值分别是( )
A. B. C. D.
4.若与是同类项,则x,y的值分别是( )
A. B. C. D.
5.已知x,y满足方程组则x+y的值为( )
A.-2 B.2 C.-4 D.4
6.如图1,在一个三角形三个顶点和中心处的每个“○”中各填有一个式子,如果图中任意三个“○”中的式子之和均相等,那么a的值为( )
A.1 B.2 C.3 D.0
图1 图2
7.如图2,一次函数y=kx+b与y=x+2的图象相交于点P(m,4),则关于x,y的二元一次方程组的解是( )
A. B. C. D.
8. 2019年足球亚洲杯在阿联酋举行,这项起源于我国“蹴鞠”的运动项目近年来在我国中小学校园得到大力推广,某次校园足球比赛规定:胜一场得3分,平一场得1分,负一场得0分,某足球队共进行了8场比赛,得了12分,该队获胜的场数有几种可能( )
A.3 B.4 C.5 D.6
9.已知关于x,y的方程组给出下列结论:①是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4-a的解.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
10.《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题4分,共24分)
11.若3x2a-3-5yb+3=8是关于x,y的二元一次方程,则a= ,b= .
12.写出一个解为的二元一次方程组 .
13.已知|2x-3y+4|与(x-2y+5)2互为相反数,则(x-y)2018= .
14.已知和是二元一次方程ax+by+3=0的两个解,则一次函数y=ax+b(a≠0)的表达式为 .
15. 对于有理数a,b定义新运算:a◎b=ax+by,其中x,y是常数.若1◎2=1,(-3)◎3=6,则2◎(-5)的值是 .
16.某旅行团到森林游乐区参观,下表为两种参观方式与所需的缆车费用:
参观方式 缆车费用
去程及回程均搭乘缆车 300元
单程搭乘缆车,单程步行 200元
已知旅行团的每个人皆从这两种方式中选择一种,且去程有15人搭乘缆车,回程有10人搭乘缆车.若他们乘坐缆车的总花费为4100元,则此旅行团共有 人.
三、解答题(共52分)
17.(每小题3分,共6分)解方程组:
(1)
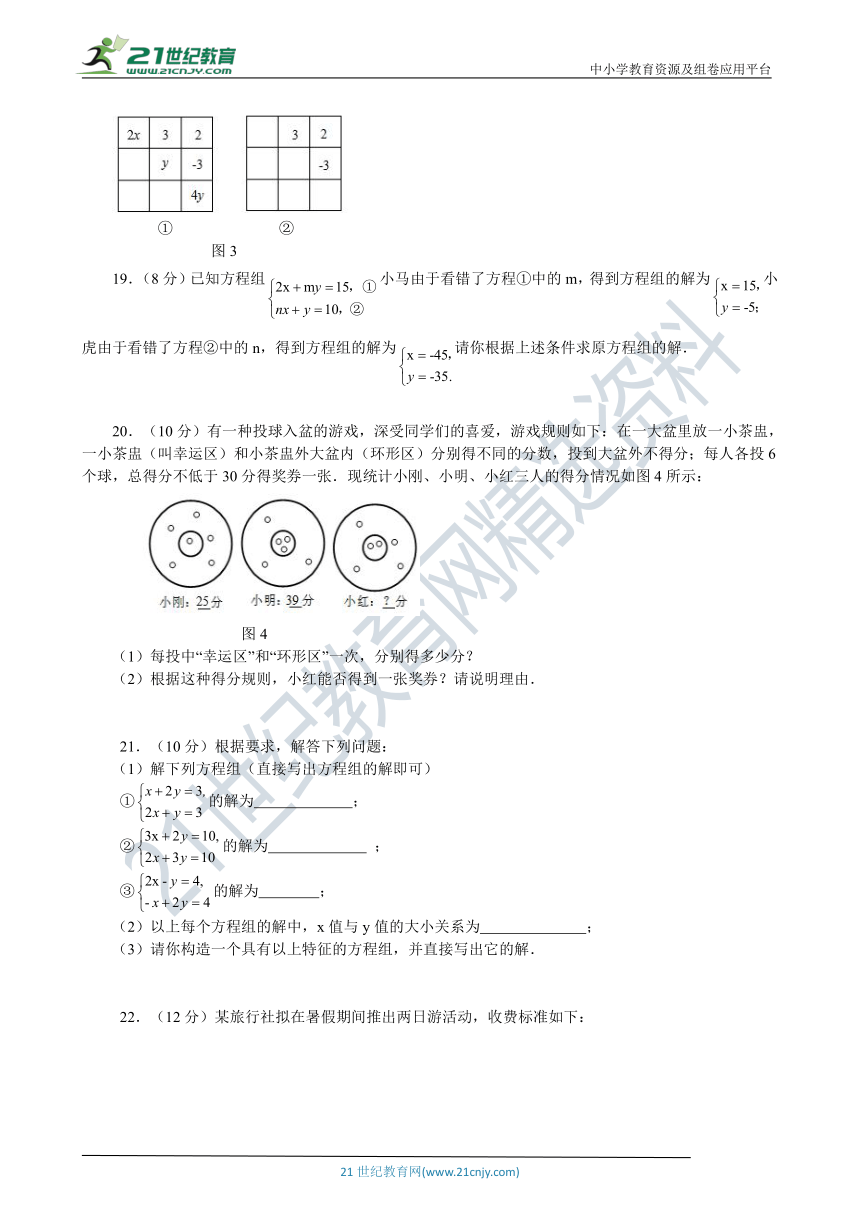
18.(6分)如图3-①,在3×3的方格内,填写了一些式子和数.
(1)若图中各行、各列及对角线上三个数之和都相等,请你求出x,y的值.
(2)把满足(1)的其他6个数填入图3-②中的方格内.
① ②
图3
19.(8分)已知方程组小马由于看错了方程①中的m,得到方程组的解为小虎由于看错了方程②中的n,得到方程组的解为请你根据上述条件求原方程组的解.
20.(10分)有一种投球入盆的游戏,深受同学们的喜爱,游戏规则如下:在一大盆里放一小茶盅,一小茶盅(叫幸运区)和小茶盅外大盆内(环形区)分别得不同的分数,投到大盆外不得分;每人各投6个球,总得分不低于30分得奖券一张.现统计小刚、小明、小红三人的得分情况如图4所示:
图4
(1)每投中“幸运区”和“环形区”一次,分别得多少分?
(2)根据这种得分规则,小红能否得到一张奖券?请说明理由.
21.(10分)根据要求,解答下列问题:
(1)解下列方程组(直接写出方程组的解即可)
①的解为 ;
②的解为 ;
③的解为 ;
(2)以上每个方程组的解中,x值与y值的大小关系为 ;
(3)请你构造一个具有以上特征的方程组,并直接写出它的解.
22.(12分)某旅行社拟在暑假期间推出两日游活动,收费标准如下:
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于120人,乙校报名参加的学生人数少于120人.经核算,若两校分别组团共需花费41 600元,若两校联合组团只需花费36 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗?为什么?
(2)两所学校报名参加旅游的学生各有多少人?
附加题(20分,不计入总分)
23.已知A,B两地相距60 km,甲、乙两人沿同一公路从A地出发到B地,甲骑摩托车,乙骑自行车,图5中CD,OE分别表示甲、乙离开A地的距离y(km)与乙离开的时间x(h)的函数关系的图象,结合图象解答下列问题.
(1)甲比乙晚出发 小时,乙的速度是 km/h;
(2)甲到达B地后,原地休息0.5 h,从B地以原来的速度和路线返回A地.
①求甲、乙两人第二次相遇时距离A地多少千米?
②求甲在整个过程中与乙相距10 km时,对应x的值.
图5
第七章 二元一次方程组达标测试卷
一、1.D 2.D 3.C 4.C 5.D 6.A 7.C 8.A 9.C 10.A
二、11.2 -2 12.答案不唯一,如
13.1 14.y=-x- 15.-7
16.16 提示:设此旅行团单程搭乘缆车,单程步行的有x人,去程及回程均搭乘缆车的有y人,根据题意,得解得所以总人数为7+9=16(人).
三、17.(1) (2)
18.解:(1)由题意,得 解得
(2)填图如下:
19.解:由题意,得解得
所以原方程组为解得
20.解:(1)设投中“幸运区”一次得x分,投中“环形区”一次得y分.
根据题意,得解得
所以投中“幸运区”一次得10分,投中“环形区”一次得3分.
(2)小红的得分为:2×10+4×3=32(分).
因为32>30,所以根据这种得分规则,小红能得到一张奖券.
21.解:(1)① ② ③
(2)x=y
(3)答案不唯一,如的解为
22.解:(1)设两校人数之和为S.
若S>200,则S=36000÷150=240;
若120<S≤200,则S=36000÷170=211,不合题意.
所以两所学校报名参加旅游的学生人数之和等于240,超过200人.
(2)设甲校报名参加旅游的学生有x人,乙校报名参加旅游的学生有y人.
①当120<x≤200时,得 解得
②当x>200时,得 解得(不合题意,舍去).
答:甲校报名参加旅游的学生有160人,乙校报名参加旅游的学生有80人.
23.解:(1)1 15
(2)①设乙出发x小时,两人第二次相遇.依题意得15x+60(x-1.5)=60×2,解得x=.
15×=42(km).
所以甲、乙两人第二次相遇时距离A地42千米.
②设OE所在直线的表达式为y=k1x,将(2,30)代入,得30=2k1,解得k1=15.
所以OE所在直线的表达式为y=15x.
设CD所在直线的表达式为y=k2x+b2,则解得
所以CD所在直线的表达式为y=60x-60.
设甲在返回时对应的函数表达式为y=k3x+b3,则解得
所以甲在返回时对应的函数表达式为y=-60x+210.
分三种情况:
①甲到达B地之前相距10 km,则|15x-(60x-60)|=10,解得 x=或x=;
②甲到达B地之后返回时相距10 km,则|15x-(-60x+210)|=10,解得 x=或x=;
③甲没出发时乙开出10千米.此时时间为
综上所述,甲在整个过程中与乙相距10 km时,对应x的值分别为,,,或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第七章 二元一次方程组达标测试卷
一、选择题(每小题3分,共30分)
1.下列不是二元一次方程组的是( )
A. B. C. D.
2.用加减法解方程组时,下列解法错误的是( )
A.①×3-②×2,消去x B.①×2-②×3,消去y
C.①×(-3)+②×2,消去x D.①×2-②×(-3),消去y
3.已知关于m,n的二元一次方程5m-2n=-3,当m与n相等时,m与n的值分别是( )
A. B. C. D.
4.若与是同类项,则x,y的值分别是( )
A. B. C. D.
5.已知x,y满足方程组则x+y的值为( )
A.-2 B.2 C.-4 D.4
6.如图1,在一个三角形三个顶点和中心处的每个“○”中各填有一个式子,如果图中任意三个“○”中的式子之和均相等,那么a的值为( )
A.1 B.2 C.3 D.0
图1 图2
7.如图2,一次函数y=kx+b与y=x+2的图象相交于点P(m,4),则关于x,y的二元一次方程组的解是( )
A. B. C. D.
8. 2019年足球亚洲杯在阿联酋举行,这项起源于我国“蹴鞠”的运动项目近年来在我国中小学校园得到大力推广,某次校园足球比赛规定:胜一场得3分,平一场得1分,负一场得0分,某足球队共进行了8场比赛,得了12分,该队获胜的场数有几种可能( )
A.3 B.4 C.5 D.6
9.已知关于x,y的方程组给出下列结论:①是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4-a的解.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
10.《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题4分,共24分)
11.若3x2a-3-5yb+3=8是关于x,y的二元一次方程,则a= ,b= .
12.写出一个解为的二元一次方程组 .
13.已知|2x-3y+4|与(x-2y+5)2互为相反数,则(x-y)2018= .
14.已知和是二元一次方程ax+by+3=0的两个解,则一次函数y=ax+b(a≠0)的表达式为 .
15. 对于有理数a,b定义新运算:a◎b=ax+by,其中x,y是常数.若1◎2=1,(-3)◎3=6,则2◎(-5)的值是 .
16.某旅行团到森林游乐区参观,下表为两种参观方式与所需的缆车费用:
参观方式 缆车费用
去程及回程均搭乘缆车 300元
单程搭乘缆车,单程步行 200元
已知旅行团的每个人皆从这两种方式中选择一种,且去程有15人搭乘缆车,回程有10人搭乘缆车.若他们乘坐缆车的总花费为4100元,则此旅行团共有 人.
三、解答题(共52分)
17.(每小题3分,共6分)解方程组:
(1)
18.(6分)如图3-①,在3×3的方格内,填写了一些式子和数.
(1)若图中各行、各列及对角线上三个数之和都相等,请你求出x,y的值.
(2)把满足(1)的其他6个数填入图3-②中的方格内.
① ②
图3
19.(8分)已知方程组小马由于看错了方程①中的m,得到方程组的解为小虎由于看错了方程②中的n,得到方程组的解为请你根据上述条件求原方程组的解.
20.(10分)有一种投球入盆的游戏,深受同学们的喜爱,游戏规则如下:在一大盆里放一小茶盅,一小茶盅(叫幸运区)和小茶盅外大盆内(环形区)分别得不同的分数,投到大盆外不得分;每人各投6个球,总得分不低于30分得奖券一张.现统计小刚、小明、小红三人的得分情况如图4所示:
图4
(1)每投中“幸运区”和“环形区”一次,分别得多少分?
(2)根据这种得分规则,小红能否得到一张奖券?请说明理由.
21.(10分)根据要求,解答下列问题:
(1)解下列方程组(直接写出方程组的解即可)
①的解为 ;
②的解为 ;
③的解为 ;
(2)以上每个方程组的解中,x值与y值的大小关系为 ;
(3)请你构造一个具有以上特征的方程组,并直接写出它的解.
22.(12分)某旅行社拟在暑假期间推出两日游活动,收费标准如下:
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于120人,乙校报名参加的学生人数少于120人.经核算,若两校分别组团共需花费41 600元,若两校联合组团只需花费36 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗?为什么?
(2)两所学校报名参加旅游的学生各有多少人?
附加题(20分,不计入总分)
23.已知A,B两地相距60 km,甲、乙两人沿同一公路从A地出发到B地,甲骑摩托车,乙骑自行车,图5中CD,OE分别表示甲、乙离开A地的距离y(km)与乙离开的时间x(h)的函数关系的图象,结合图象解答下列问题.
(1)甲比乙晚出发 小时,乙的速度是 km/h;
(2)甲到达B地后,原地休息0.5 h,从B地以原来的速度和路线返回A地.
①求甲、乙两人第二次相遇时距离A地多少千米?
②求甲在整个过程中与乙相距10 km时,对应x的值.
图5
第七章 二元一次方程组达标测试卷
一、1.D 2.D 3.C 4.C 5.D 6.A 7.C 8.A 9.C 10.A
二、11.2 -2 12.答案不唯一,如
13.1 14.y=-x- 15.-7
16.16 提示:设此旅行团单程搭乘缆车,单程步行的有x人,去程及回程均搭乘缆车的有y人,根据题意,得解得所以总人数为7+9=16(人).
三、17.(1) (2)
18.解:(1)由题意,得 解得
(2)填图如下:
19.解:由题意,得解得
所以原方程组为解得
20.解:(1)设投中“幸运区”一次得x分,投中“环形区”一次得y分.
根据题意,得解得
所以投中“幸运区”一次得10分,投中“环形区”一次得3分.
(2)小红的得分为:2×10+4×3=32(分).
因为32>30,所以根据这种得分规则,小红能得到一张奖券.
21.解:(1)① ② ③
(2)x=y
(3)答案不唯一,如的解为
22.解:(1)设两校人数之和为S.
若S>200,则S=36000÷150=240;
若120<S≤200,则S=36000÷170=211,不合题意.
所以两所学校报名参加旅游的学生人数之和等于240,超过200人.
(2)设甲校报名参加旅游的学生有x人,乙校报名参加旅游的学生有y人.
①当120<x≤200时,得 解得
②当x>200时,得 解得(不合题意,舍去).
答:甲校报名参加旅游的学生有160人,乙校报名参加旅游的学生有80人.
23.解:(1)1 15
(2)①设乙出发x小时,两人第二次相遇.依题意得15x+60(x-1.5)=60×2,解得x=.
15×=42(km).
所以甲、乙两人第二次相遇时距离A地42千米.
②设OE所在直线的表达式为y=k1x,将(2,30)代入,得30=2k1,解得k1=15.
所以OE所在直线的表达式为y=15x.
设CD所在直线的表达式为y=k2x+b2,则解得
所以CD所在直线的表达式为y=60x-60.
设甲在返回时对应的函数表达式为y=k3x+b3,则解得
所以甲在返回时对应的函数表达式为y=-60x+210.
分三种情况:
①甲到达B地之前相距10 km,则|15x-(60x-60)|=10,解得 x=或x=;
②甲到达B地之后返回时相距10 km,则|15x-(-60x+210)|=10,解得 x=或x=;
③甲没出发时乙开出10千米.此时时间为
综上所述,甲在整个过程中与乙相距10 km时,对应x的值分别为,,,或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
