鲁教版数学七年级下册 期末达标测试卷(含答案)
文档属性
| 名称 | 鲁教版数学七年级下册 期末达标测试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 17:57:27 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末达标测试卷
一、选择题(本大题共10小题,每小题3分,共30分)
1.冬季奥林匹克运动会是世界规模最大的冬季综合性运动会,每四年举办一次,第24届冬奥会将于2022年在北京和张家口举办.下列四个图案分别是第24届冬奥会图标中的一部分,其中是轴对称图形的是( )
A B C D
2.下列说法中,错误的是( )
A.9的算术平方根是3 B.的平方根是±2
C.8的立方根是±2 D.-1的立方根等于-1
3.蝴蝶标本可以近似地看做轴对称图形,如图1,将一只蝴蝶标本放在平面直角坐标系中,如果图中点A的坐标为(-5,3),则其关于y轴对称的点B的坐标为( )
A.(5,3) B.(5,-3) C.(-5,-3) D.(3,5)
图1 图2
4.(2021年达州)实数+1在图2所示数轴上的对应点可能是( )
A.点A B.点B C.点C D.点D
5.(2021年烟台,改编)如图3,在平面直角坐标系中,四边形ABCD的顶点A,B分别在y轴和x轴上,且AB∥CD.若点B的坐标为(-1,0),∠BCD=120°,则点A的坐标为( )
A.(,0) B.(0,2) C.(0,) D.(0,1)
图3 图4
6.如图4,在△ABC中,AB=BC,顶点B在y轴上,顶点C的坐标为(2,0),若一次函数y=kx+2的图象经过点A,则k的值为( )
A. B.- C.1 D.-1
7.在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几.”此问题可理解为:如图5,有一架秋千,当它静止时,踏板离地距离AB长度为1尺.将它往前水平推送10尺时,即A′C=10尺,则此时秋千的踏板离地距离A′D就和身高5尺的人一样高.若运动过程中秋千的绳索始终拉得很直,则绳索OA长为( )
A.13.5尺 B.14尺 C.14.5尺 D.15尺
图5 图6
8.如图6,在△ABC中,AQ=PQ,AP平分∠BAC,PR⊥AB于点R,PS⊥AC于点S,下列结论:①AR=AS;②QP∥AR;③△BPR≌△QPS.其中一定正确的是( )
A.①②③ B.仅①② C.仅① D.仅①③
9.图7所示的三角形中,若AB=AC,则能被一条线段分成两个小等腰三角形的是( )
A.①②③ B.①②④ C.②③④ D.①③④
图7
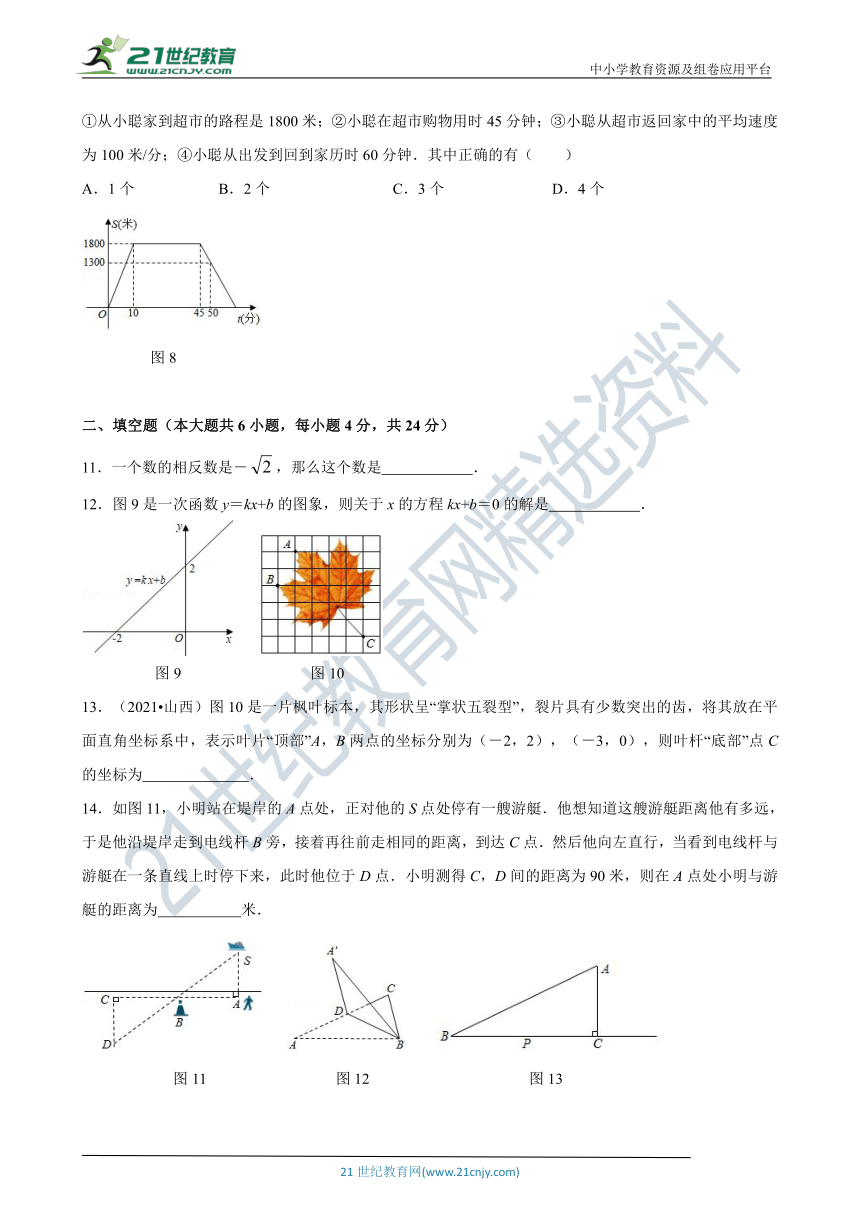
10.小聪上午8:00从家里出发骑“共享单车”去一家超市购物,然后从这家超市原路返中,小聪离家的路程s(米)和经过的时间t(分)之间的函数关系如图8所示,有下列说法:
①从小聪家到超市的路程是1800米;②小聪在超市购物用时45分钟;③小聪从超市返回家中的平均速度为100米/分;④小聪从出发到回到家历时60分钟.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
图8
二、填空题(本大题共6小题,每小题4分,共24分)
11.一个数的相反数是-,那么这个数是 .
12.图9是一次函数y=kx+b的图象,则关于x的方程kx+b=0的解是 .
图9 图10
13.(2021 山西)图10是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿,将其放在平面直角坐标系中,表示叶片“顶部”A,B两点的坐标分别为(-2,2),(-3,0),则叶杆“底部”点C的坐标为 .
14.如图11,小明站在堤岸的A点处,正对他的S点处停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离,到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.小明测得C,D间的距离为90米,则在A点处小明与游艇的距离为 米.
图11 图12 图13
15.如图12所示,在△ABC中,∠C=80°,AC边上有一点D,使得∠A=∠ABD,将△ABC沿BD翻折得△A′BD,此时A′D∥BC,则∠ABC的度数为 .
16.如图13,在Rt△ACB中,∠ACB=90°,AB=13,AC=5,动点P从点B出发沿射线BC运动,当△APB为等腰三角形时,这个三角形底边的长为 .
三、解答题(本大题共7小题,共66分)
17.(每小题3分,共6分)计算:
(1)+-+|1-|; (2)-+|-2|.
18.(8分)如图14,已知:∠α,∠β,线段c,求作:△ABC,使∠A=∠α,∠B=∠β,AB=c.(不写作法,保留作图痕迹)
图14
19.(8分)如图15,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,4),
B(4,2),C(3,5),请回答下列问题:
(1)写出△ABC关于x轴的对称图形△A1B1C1的顶点坐标.(2)求△ABC的面积.
图15 图16
20.(8分)如图16,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E,F.
(1)试说明:DE=DF;(2)若∠BDE=55°,求∠BAC的度数.
21.(10分)如图17,圆柱形玻璃容器高19 cm,底面周长为60 cm,在外侧距下底1.5 cm的点A处有一只蜘蛛,距蜘蛛正对面的圆柱形容器的上底1.5 cm处的点B处有一只苍蝇,蜘蛛急于捕捉苍蝇充饥,请你帮蜘蛛计算它沿容器侧面爬行的最短距离.
图17 图18
22.(12分)如图18,在△ABC中,AC=BC,点D为△ABC内一点,且CD恰好平分∠ACB,E为AD延长线上一点,CE=CA.
(1)△ACD和△BCD全等吗?为什么?
(2)若∠ACD=40°,∠CBD=15°,求∠BAD的度数;
(3)点F在DE上,连接CF,若CD=CF,试说明:EF=BD.
23.(14分)如图19,在平面直角坐标系中,过点C(0,12)的直线AC与直线OA相交于点A(8,4).
(1)求直线AC的函数表达式;
(2)求△OAC的面积;
(3)动点M在线段OA和射线AC上运动,是否存在点M,使△OMC的面积是△OAC面积的?若存在,求出此时点M的坐标;若不存在,请说明理由.
图19
期末达标测试卷参考答案:
一、1.C 2.C 3.A 4.D 5.C 6.C 7.C 8.B 9.D 10.B
二、11. 12.x=-2 13.(2,-3)
14.90 15.75° 16.24或 或13
三、17.解:(1)原式=4+(-2)-+-1=1;
(2)原式=-+2-=-+2-=1-.
18.解:如图1所示,△ABC即为所求作.
图1
19.解:(1)△ABC关于x轴的对称图形△A1B1C1的顶点坐标分别为A1(1,-4),B1(4,-2),C1(3,-5);
(2)△ABC的面积为3×3-×1×2-×1×3-×2×3=9-1-1.5-3=3.5.
20.解:(1)因为点D是BC的中点,所以BD=CD.在△BED和△CFD中,因为∠BED=∠CFD=90°,∠B=∠C,BD=CD,所以△BED≌△△CFD(AAS).所以DE=DF.
(2)因为DE⊥AB,所以∠BED=90°.因为∠BDE=55°,所以∠B=35°,所以∠C=35°.所以∠BAC=110°.
21.解:如图2,将圆柱侧面展开成长方形MNQP,过点B作BC⊥MN于点C,连接AB,则线段AB的长度即为最短距离.在Rt△ACB中,AC=MN-AN-CM=19-1.5-1.5=16(cm),BC的长为底面圆周的一半长,即BC=30 cm.由勾股定理,得AB2=AC2+BC2=162+302=1156=342,所以AB=34 cm.所以蜘蛛所走的最短距离为34 cm.
图2
22.解:(1)△ACD≌△BCD.理由如下:因为CD平分∠ACB,所以∠ACD=∠BCD.在△ACD和△BCD中,因为AC=BC,∠ACD=∠BCD,CD=CD,所以△ACD≌△BCD.
(2)因为△ACD≌△BCD,所以∠CAD=∠CBD=15°,∠BCD=∠ACD=40°,AD=BD.
所以∠DAB=∠DBA.所以∠BAD=(180°-2∠CAD-2∠ACD)=35°.
(3)因为CD=CF,所以∠CDF=∠CFD,所以∠ADC=∠EFC.因为CA=CE,所以∠CAD=∠CEF.在△CAD和△CEF中,因为∠ADC=∠EFC,∠CAD=∠CEF,CA=CE,所以△CAD≌△CEF,所以AD=EF.因为AD=BD,所以EF=BD.
23.解:(1)设直线AC的函数表达式为y=kx+b,因为直线经过点C(0,12),所以b=12,所以函数表达式为y=kx+12.
又因为直线经过点A(8,4),所以8k+12=4,解得k=-1,所以直线AC的函数表达式为y=-x+12.
(2)因为点A的坐标为(8,4),所以OC边上的高为h=8.因为点C的坐标为(0,12),所以OC=12,所以S△OAC=OC h=×12×8=48.
(3)存在,分情况讨论如下:
①如图3,若M在线段OA上时,△OMC的面积是△OAC面积的,所以M为OA中点,因为点A的坐标为(8,4),所以点M的坐标为(4,2);
图3 图4
②如图4,当M在射线AC上时,因为△OMC的面积是△OAC面积的,所以M为AC的中点,而A(8,4),C(0,12),所以点M坐标为(4,8).由等底同高的三角形面积相等可知,若M在点C的右侧,即射线AC上的点M'处,CM'=CM时,△OM'C的面积也等于△OAC面积的,此时点C为线段MM'的中点,而C(0,12),M(4,8),所以点M'坐标为(-4,16).
综上所述,点M的坐标为(4,2)或(4,8)或(-4,16).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
期末达标测试卷
一、选择题(本大题共10小题,每小题3分,共30分)
1.冬季奥林匹克运动会是世界规模最大的冬季综合性运动会,每四年举办一次,第24届冬奥会将于2022年在北京和张家口举办.下列四个图案分别是第24届冬奥会图标中的一部分,其中是轴对称图形的是( )
A B C D
2.下列说法中,错误的是( )
A.9的算术平方根是3 B.的平方根是±2
C.8的立方根是±2 D.-1的立方根等于-1
3.蝴蝶标本可以近似地看做轴对称图形,如图1,将一只蝴蝶标本放在平面直角坐标系中,如果图中点A的坐标为(-5,3),则其关于y轴对称的点B的坐标为( )
A.(5,3) B.(5,-3) C.(-5,-3) D.(3,5)
图1 图2
4.(2021年达州)实数+1在图2所示数轴上的对应点可能是( )
A.点A B.点B C.点C D.点D
5.(2021年烟台,改编)如图3,在平面直角坐标系中,四边形ABCD的顶点A,B分别在y轴和x轴上,且AB∥CD.若点B的坐标为(-1,0),∠BCD=120°,则点A的坐标为( )
A.(,0) B.(0,2) C.(0,) D.(0,1)
图3 图4
6.如图4,在△ABC中,AB=BC,顶点B在y轴上,顶点C的坐标为(2,0),若一次函数y=kx+2的图象经过点A,则k的值为( )
A. B.- C.1 D.-1
7.在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几.”此问题可理解为:如图5,有一架秋千,当它静止时,踏板离地距离AB长度为1尺.将它往前水平推送10尺时,即A′C=10尺,则此时秋千的踏板离地距离A′D就和身高5尺的人一样高.若运动过程中秋千的绳索始终拉得很直,则绳索OA长为( )
A.13.5尺 B.14尺 C.14.5尺 D.15尺
图5 图6
8.如图6,在△ABC中,AQ=PQ,AP平分∠BAC,PR⊥AB于点R,PS⊥AC于点S,下列结论:①AR=AS;②QP∥AR;③△BPR≌△QPS.其中一定正确的是( )
A.①②③ B.仅①② C.仅① D.仅①③
9.图7所示的三角形中,若AB=AC,则能被一条线段分成两个小等腰三角形的是( )
A.①②③ B.①②④ C.②③④ D.①③④
图7
10.小聪上午8:00从家里出发骑“共享单车”去一家超市购物,然后从这家超市原路返中,小聪离家的路程s(米)和经过的时间t(分)之间的函数关系如图8所示,有下列说法:
①从小聪家到超市的路程是1800米;②小聪在超市购物用时45分钟;③小聪从超市返回家中的平均速度为100米/分;④小聪从出发到回到家历时60分钟.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
图8
二、填空题(本大题共6小题,每小题4分,共24分)
11.一个数的相反数是-,那么这个数是 .
12.图9是一次函数y=kx+b的图象,则关于x的方程kx+b=0的解是 .
图9 图10
13.(2021 山西)图10是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿,将其放在平面直角坐标系中,表示叶片“顶部”A,B两点的坐标分别为(-2,2),(-3,0),则叶杆“底部”点C的坐标为 .
14.如图11,小明站在堤岸的A点处,正对他的S点处停有一艘游艇.他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆B旁,接着再往前走相同的距离,到达C点.然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于D点.小明测得C,D间的距离为90米,则在A点处小明与游艇的距离为 米.
图11 图12 图13
15.如图12所示,在△ABC中,∠C=80°,AC边上有一点D,使得∠A=∠ABD,将△ABC沿BD翻折得△A′BD,此时A′D∥BC,则∠ABC的度数为 .
16.如图13,在Rt△ACB中,∠ACB=90°,AB=13,AC=5,动点P从点B出发沿射线BC运动,当△APB为等腰三角形时,这个三角形底边的长为 .
三、解答题(本大题共7小题,共66分)
17.(每小题3分,共6分)计算:
(1)+-+|1-|; (2)-+|-2|.
18.(8分)如图14,已知:∠α,∠β,线段c,求作:△ABC,使∠A=∠α,∠B=∠β,AB=c.(不写作法,保留作图痕迹)
图14
19.(8分)如图15,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,4),
B(4,2),C(3,5),请回答下列问题:
(1)写出△ABC关于x轴的对称图形△A1B1C1的顶点坐标.(2)求△ABC的面积.
图15 图16
20.(8分)如图16,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E,F.
(1)试说明:DE=DF;(2)若∠BDE=55°,求∠BAC的度数.
21.(10分)如图17,圆柱形玻璃容器高19 cm,底面周长为60 cm,在外侧距下底1.5 cm的点A处有一只蜘蛛,距蜘蛛正对面的圆柱形容器的上底1.5 cm处的点B处有一只苍蝇,蜘蛛急于捕捉苍蝇充饥,请你帮蜘蛛计算它沿容器侧面爬行的最短距离.
图17 图18
22.(12分)如图18,在△ABC中,AC=BC,点D为△ABC内一点,且CD恰好平分∠ACB,E为AD延长线上一点,CE=CA.
(1)△ACD和△BCD全等吗?为什么?
(2)若∠ACD=40°,∠CBD=15°,求∠BAD的度数;
(3)点F在DE上,连接CF,若CD=CF,试说明:EF=BD.
23.(14分)如图19,在平面直角坐标系中,过点C(0,12)的直线AC与直线OA相交于点A(8,4).
(1)求直线AC的函数表达式;
(2)求△OAC的面积;
(3)动点M在线段OA和射线AC上运动,是否存在点M,使△OMC的面积是△OAC面积的?若存在,求出此时点M的坐标;若不存在,请说明理由.
图19
期末达标测试卷参考答案:
一、1.C 2.C 3.A 4.D 5.C 6.C 7.C 8.B 9.D 10.B
二、11. 12.x=-2 13.(2,-3)
14.90 15.75° 16.24或 或13
三、17.解:(1)原式=4+(-2)-+-1=1;
(2)原式=-+2-=-+2-=1-.
18.解:如图1所示,△ABC即为所求作.
图1
19.解:(1)△ABC关于x轴的对称图形△A1B1C1的顶点坐标分别为A1(1,-4),B1(4,-2),C1(3,-5);
(2)△ABC的面积为3×3-×1×2-×1×3-×2×3=9-1-1.5-3=3.5.
20.解:(1)因为点D是BC的中点,所以BD=CD.在△BED和△CFD中,因为∠BED=∠CFD=90°,∠B=∠C,BD=CD,所以△BED≌△△CFD(AAS).所以DE=DF.
(2)因为DE⊥AB,所以∠BED=90°.因为∠BDE=55°,所以∠B=35°,所以∠C=35°.所以∠BAC=110°.
21.解:如图2,将圆柱侧面展开成长方形MNQP,过点B作BC⊥MN于点C,连接AB,则线段AB的长度即为最短距离.在Rt△ACB中,AC=MN-AN-CM=19-1.5-1.5=16(cm),BC的长为底面圆周的一半长,即BC=30 cm.由勾股定理,得AB2=AC2+BC2=162+302=1156=342,所以AB=34 cm.所以蜘蛛所走的最短距离为34 cm.
图2
22.解:(1)△ACD≌△BCD.理由如下:因为CD平分∠ACB,所以∠ACD=∠BCD.在△ACD和△BCD中,因为AC=BC,∠ACD=∠BCD,CD=CD,所以△ACD≌△BCD.
(2)因为△ACD≌△BCD,所以∠CAD=∠CBD=15°,∠BCD=∠ACD=40°,AD=BD.
所以∠DAB=∠DBA.所以∠BAD=(180°-2∠CAD-2∠ACD)=35°.
(3)因为CD=CF,所以∠CDF=∠CFD,所以∠ADC=∠EFC.因为CA=CE,所以∠CAD=∠CEF.在△CAD和△CEF中,因为∠ADC=∠EFC,∠CAD=∠CEF,CA=CE,所以△CAD≌△CEF,所以AD=EF.因为AD=BD,所以EF=BD.
23.解:(1)设直线AC的函数表达式为y=kx+b,因为直线经过点C(0,12),所以b=12,所以函数表达式为y=kx+12.
又因为直线经过点A(8,4),所以8k+12=4,解得k=-1,所以直线AC的函数表达式为y=-x+12.
(2)因为点A的坐标为(8,4),所以OC边上的高为h=8.因为点C的坐标为(0,12),所以OC=12,所以S△OAC=OC h=×12×8=48.
(3)存在,分情况讨论如下:
①如图3,若M在线段OA上时,△OMC的面积是△OAC面积的,所以M为OA中点,因为点A的坐标为(8,4),所以点M的坐标为(4,2);
图3 图4
②如图4,当M在射线AC上时,因为△OMC的面积是△OAC面积的,所以M为AC的中点,而A(8,4),C(0,12),所以点M坐标为(4,8).由等底同高的三角形面积相等可知,若M在点C的右侧,即射线AC上的点M'处,CM'=CM时,△OM'C的面积也等于△OAC面积的,此时点C为线段MM'的中点,而C(0,12),M(4,8),所以点M'坐标为(-4,16).
综上所述,点M的坐标为(4,2)或(4,8)或(-4,16).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
