鲁教版数学七年级下册 期中达标测试卷(含答案)
文档属性
| 名称 | 鲁教版数学七年级下册 期中达标测试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 18:00:21 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期中达标测试卷
一、选择题(本大题共10小题,每小题3分,共30分)
1.已知两根木棒的长度如图1所示,要选择第三根木棒,使之与这两根木棒组成一个三角形,则第三根木棒的长度可以是( )
A.2 cm B.3 cm C.6 cm D.9 cm
图1 图2 图3
2.体育运动不仅能增强人的体质,对人智力的提升也有一定的促进作用.下列体育运动图片是轴对称图形的是( )
A B C D
3.如图2,在△ABC和△DCB中,AB=DC,∠ABC=∠DCB,那么能直接判断△ABC≌△DCB的方法是( )
A.SAS B.AAS C.SSS D.ASA
4.已知△ABC的三边长分别是a,b,c,且满足等式,则△ABC是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.等腰直角三角形
5.如图3,在等腰三角形ABC中,AB=BC,点D在AC上,且∠DBC=90 ,若∠BDC=α,试用含α的代数式表示∠ABD的结果为( )
A.180 -α B.180 -2α C.3α-90 D.2α-90
6.如图4所示,把一张正方形纸片三次对折后沿着虚线剪下,将剩余部分展开所得的图形是( )
图4
7.如图5,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DE=3,AB=6,AC=4,则S△ABC为( )
A.16 B.15 C.14 D.13
图5 图6
8.图6-①是几何鱼的图片,图6-②是它的部分示意图.在△CEF中,∠E=80 ,∠F=50 ,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数为( )
A.50 B.55 C.60 D.65
9.如图7,小斌制作了一个底面直径为 cm,高为4 cm的圆柱体粮仓模型,其中BC是底面直径,AB是高,现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A,C两点(接头不计),则装饰带的长度最短为( )
A.10 cm B.12 cm C.14 cm D.16 cm
图7 图8
10.如图8,在四边形ABCD中,∠D=90 ,AD=4,DC=3,连接AC,分别以点A,C为圆心,以大于AC为半径作弧,两弧交于点E,作射线BE交AC于点O,交AD于点F,O是AC的中点,AD∥BC,下列结论:①△AOF≌△COB;②AC平分∠BAD;③BC的长为3.其中正确的有( )
A.3个 B.2个 C.1个 D.0个
二、填空题(本大题共6小题,每小题3分,共18分)
11.如图9,点C是线段BD的中点,∠B=90 ,∠A=30 ,CD=2,则AC的长为 .
图9 图10 图11
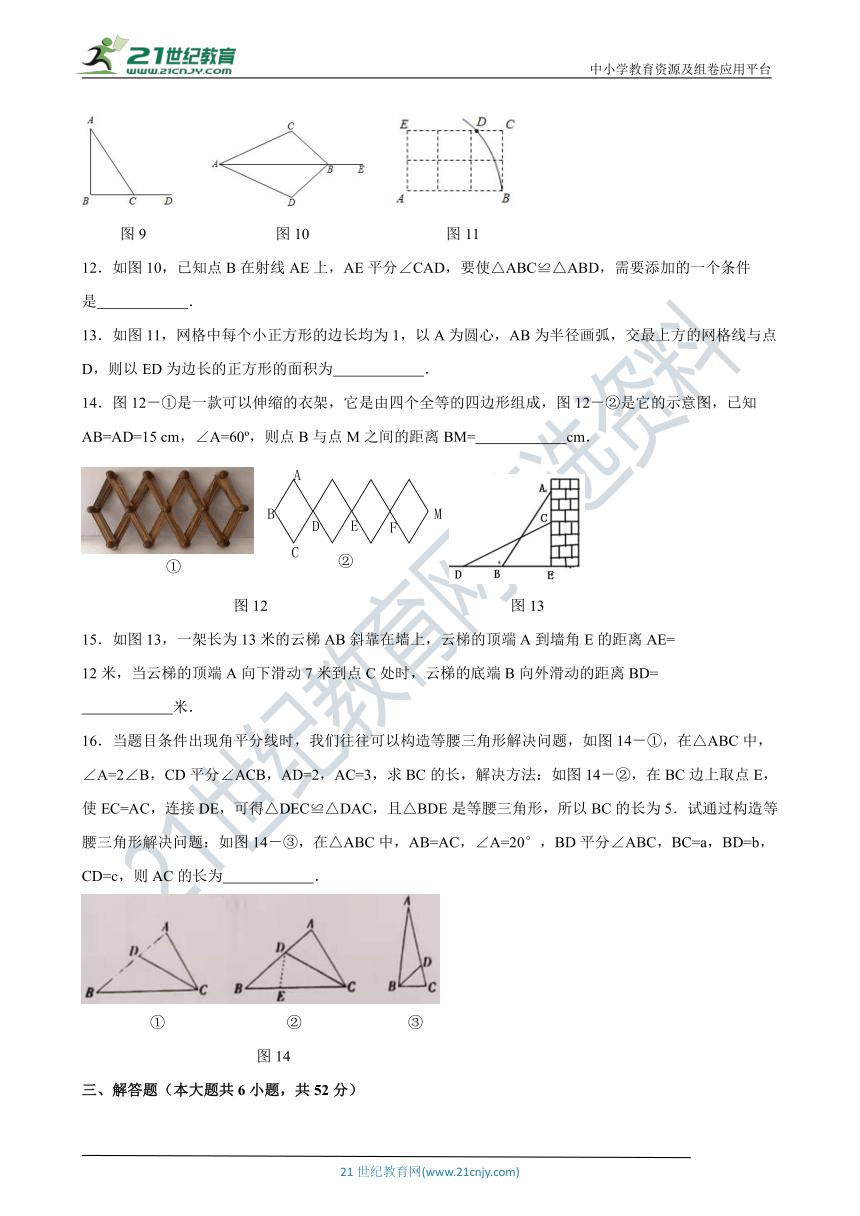
12.如图10,已知点B在射线AE上,AE平分∠CAD,要使△ABC≌△ABD,需要添加的一个条件是 .
13.如图11,网格中每个小正方形的边长均为1,以A为圆心,AB为半径画弧,交最上方的网格线与点D,则以ED为边长的正方形的面积为 .
14.图12-①是一款可以伸缩的衣架,它是由四个全等的四边形组成,图12-②是它的示意图,已知AB=AD=15 cm,∠A=60 ,则点B与点M之间的距离BM= cm.
图12 图13
15.如图13,一架长为13米的云梯AB斜靠在墙上,云梯的顶端A到墙角E的距离AE=
12米,当云梯的顶端A向下滑动7米到点C处时,云梯的底端B向外滑动的距离BD=
米.
16.当题目条件出现角平分线时,我们往往可以构造等腰三角形解决问题,如图14-①,在△ABC中,∠A=2∠B,CD平分∠ACB,AD=2,AC=3,求BC的长,解决方法:如图14-②,在BC边上取点E,使EC=AC,连接DE,可得△DEC≌△DAC,且△BDE是等腰三角形,所以BC的长为5.试通过构造等腰三角形解决问题:如图14-③,在△ABC中,AB=AC,∠A=20°,BD平分∠ABC,BC=a,BD=b,CD=c,则AC的长为 .
① ② ③
图14
三、解答题(本大题共6小题,共52分)
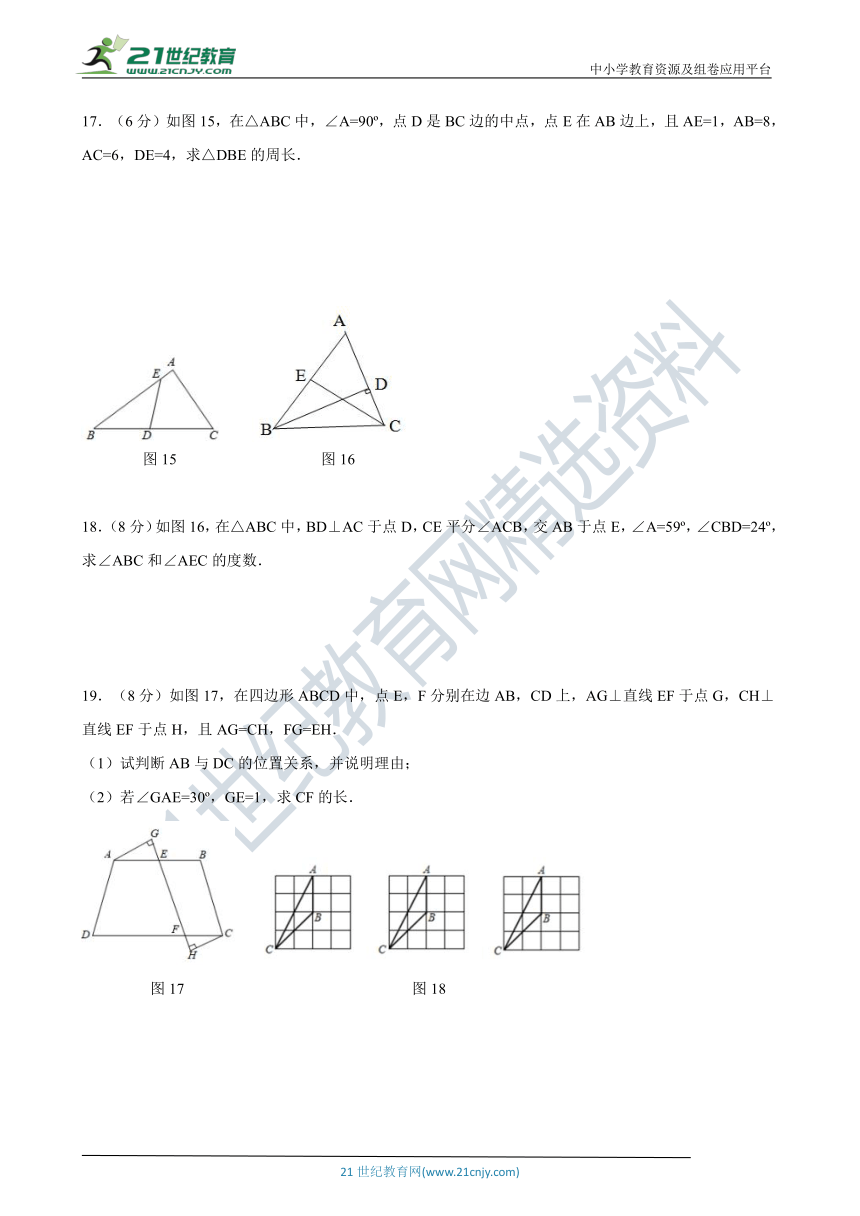
17.(6分)如图15,在△ABC中,∠A=90 ,点D是BC边的中点,点E在AB边上,且AE=1,AB=8,AC=6,DE=4,求△DBE的周长.
图15 图16
18.(8分)如图16,在△ABC中,BD⊥AC于点D,CE平分∠ACB,交AB于点E,∠A=59 ,∠CBD=24 ,求∠ABC和∠AEC的度数.
19.(8分)如图17,在四边形ABCD中,点E,F分别在边AB,CD上,AG⊥直线EF于点G,CH⊥直线EF于点H,且AG=CH,FG=EH.
(1)试判断AB与DC的位置关系,并说明理由;
(2)若∠GAE=30 ,GE=1,求CF的长.
图17 图18
20.(8分)在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)求格点△ABC的面积;
(2)请你在图中画出与△ABC成轴对称的格点三角形(画出3个即可).
21.(10分)中国古代数学家们对于勾股定理的发现和验证,在世界数学史上具有独特的发现和地位.现由4个全等的直角三角形构成了如图19所示的“弦图”,在Rt△ABC中,AC=b,BC=a,AB=c,请你利用这个图形解答下列问题:
(1)试说明:a2+b2=c2;
(2)如果大正方形的面积为10,小正方形的面积为2,求(a+b)2的值.
图19 图20
22.(12分)如图20,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:(1)如果把以上问题中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?说明理由.
(2)如果把以上问题中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
附加题(20分,不计入总分)
23.综合与探究:
如图21,在Rt△ABC中,∠B=90 ,AB=8 cm,AC=10 cm,动点P从点A出发,沿着A→B的方向运动,且速度为cm/s,动点Q从B出发,沿着B→C→A的方向运动,且速度为每秒1 cm/s,它们同时出发,设出发的时间为t s.
(1)当t=4 s时,求△PBQ的面积;
(2)点P在边AB上运动的过程中,若点P正好落在斜边AC的垂直平分线上,求此时t的值,并求出此时CQ的长;
(3)若点Q在斜边AC上运动过程中,是否存在t的值,使得△BCQ恰好是等腰三角形,若存在,求出所有t的值;若不存在,请说明理由.
图21
期中达标测试卷参考答案:
一、1.C 2.C 3.A 4.B 5.D 6.C 7.B 8.A 9.A 10.B
二、11.4 12.答案不唯一,如AC=AD 13.5 14.60 15.7
16.a+b+c 提示:如图1所示,因为△ABC中,AB=AC,∠A=20°,所以∠ABC=
∠C=80°.因为BD平分∠ABC,所以∠1=∠2=40°,∠BDC=60°.在BA边上取点E,使BE=BC=a,连接DE,易得△DBE≌△DBC(SAS).所以∠BED=∠C=80°.所以∠4=
60°.所以∠3=60°.在DA边上取点F,使DF=DB,连接FE,易得△BDE≌△FDE(SAS).所以∠5=∠1=40°,FE=BE= a.因为∠A=20°,所以∠6=20°,所以AF=EF=a.因为DF=BD= b,所以AC=AF+DF+CD=a+b+c.
图1
三、17.解:在Rt△ABC中,由勾股定理,得BC2=AB2+AC2=82+62=100.因为点D是BC边的中点,所以BD=BC=5.因为AE=1,所以BE=8-1=7,所以△DBE的周长=BE+
BD+DE=7+5+4=16.
18.解:因为BD⊥AC,所以∠ADB=90 .因为∠A=59 ,所以∠ABD=90 -59 =31 .所以∠ABC=∠ABD+∠CBD=31 +24 =55 .所以∠ACB=90 -∠CBD=90 -24 =66 .因为CE平分∠ACB,所以∠ACE=∠ACB=×66 =33 .所以∠AEC=180 -∠A-∠ACE=180 -59 -33 =88 .
19.解:(1)AB∥DC.理由:因为GF=EH,所以EG=FH.因为AG=CH,∠G=∠H=90 ,所以△AGE≌△CHF(SAS) .所以∠AEG=∠CFH.因为∠AEF=180 -∠AEG,∠CFE=180 -∠CFH,所以∠AEF=∠CFE,所以AB∥CD.
(2)因为∠GAE=30 ,GE=1,所以AE=2EG=2×1=2.因为△AGE≌△CHF,所以CF=AE=2.
20.解:(1)S△ABC=×2×2=2.
(2)答案不唯一,如△ABC1,△A1BC,△DEF,画出的图形如图2所示.
图2
21.解:(1)由图可知,S正方形=4×ab+(b-a)2=2ab+a2-2ab+b2=a2+b2,S正方形=c2,所以a2+b2=c2.
(2)根据题意,得c2=10,(b-a)2=2.因为a2+b2=c2,所以a2+b2=10.因为(b-a)2=2,所以b2-2ab+a2=2,所以2ab=a2+b2-2=10-2=8,所以(a+b)2=a2+b2+2ab=10+8=18.
22.解:(1)∠DAC的度数不会改变.理由如下:
因为EA=EC,所以∠CAE=∠C.所以∠AEB=2∠C.因为BA=BD,所以∠BAD=(180°-∠B)=[180°-(90°-∠AEB)]=[180°-(90°-2∠C)]=45°+∠C,所以∠DAE=90°-∠BAD=90°-(45°+∠C)=45°-∠C.所以∠DAC=∠DAE+∠CAE=∠DAE+∠C=45°.
(2)设∠ABC=m°,则∠BAD=(180°-m°)=90°-m°,∠AEB=180°-n°-m°,所以∠DAE=∠BAE-∠BAD=n°-90°+m°.
因为EA=EC,所以∠CAE=∠AEB=90°-n°-m°,所以∠DAC=∠DAE+∠CAE=n°-90°+m°+90°-n°-m°=n°.
23.解:在Rt△ABC中,BC2=AC2-AB2=102-82=36,所以BC=6 cm.
(1)当t=4 s时,BP=AB-AP=8-4×=6 cm,BQ=4×1=4 cm,所以△PBQ的面积为×6×4=
12(cm2).
(2)因为点P正好落在斜边AC的垂直平分线上,所以PA=PC.因为PA=t,所以PC=
t,所以BP=8-t.所以在Rt△BPC中,由勾股定理,得BC2+BP2=PC2,所以62+(8-
t)2=(t)2,解得t=s.此时CQ=.
(3)存在.理由如下:分三种情况讨论:
①如图3-①,当CQ=BQ时,∠C=∠CBQ.因为∠A+∠C=90 ,∠CBQ+∠ABQ=90 ,所以∠A=∠ABQ,所以AQ=BQ.所以AQ=CQ.所以CQ= cm,所以BC+CQ=6+5=11 cm,所以t=11÷1=11.
① ②
图3
②当CQ=BC时,BC+CQ=6+6=12 cm,所以t=12÷1=12.
③如图3-②,当BC=BQ时,因为BC=6,所以BQ=6,过点B作BE⊥CQ,垂足为E.所以CQ=2CE.因为S△ABC=,所以8×6=10×BE,所以BE=.在Rt△BCE中,由勾股定理,得BC2=CE2+BE2,所以CE2=62-(.所以BC+CQ=6+2×=,所以t=.
综上所述,存在t的值为11或12或,使得△BCQ恰好是等腰三角形.
3 cm
6 cm
A
D
C
B
A
F
E
D
C
B
M
①
②
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
期中达标测试卷
一、选择题(本大题共10小题,每小题3分,共30分)
1.已知两根木棒的长度如图1所示,要选择第三根木棒,使之与这两根木棒组成一个三角形,则第三根木棒的长度可以是( )
A.2 cm B.3 cm C.6 cm D.9 cm
图1 图2 图3
2.体育运动不仅能增强人的体质,对人智力的提升也有一定的促进作用.下列体育运动图片是轴对称图形的是( )
A B C D
3.如图2,在△ABC和△DCB中,AB=DC,∠ABC=∠DCB,那么能直接判断△ABC≌△DCB的方法是( )
A.SAS B.AAS C.SSS D.ASA
4.已知△ABC的三边长分别是a,b,c,且满足等式,则△ABC是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.等腰直角三角形
5.如图3,在等腰三角形ABC中,AB=BC,点D在AC上,且∠DBC=90 ,若∠BDC=α,试用含α的代数式表示∠ABD的结果为( )
A.180 -α B.180 -2α C.3α-90 D.2α-90
6.如图4所示,把一张正方形纸片三次对折后沿着虚线剪下,将剩余部分展开所得的图形是( )
图4
7.如图5,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DE=3,AB=6,AC=4,则S△ABC为( )
A.16 B.15 C.14 D.13
图5 图6
8.图6-①是几何鱼的图片,图6-②是它的部分示意图.在△CEF中,∠E=80 ,∠F=50 ,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数为( )
A.50 B.55 C.60 D.65
9.如图7,小斌制作了一个底面直径为 cm,高为4 cm的圆柱体粮仓模型,其中BC是底面直径,AB是高,现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A,C两点(接头不计),则装饰带的长度最短为( )
A.10 cm B.12 cm C.14 cm D.16 cm
图7 图8
10.如图8,在四边形ABCD中,∠D=90 ,AD=4,DC=3,连接AC,分别以点A,C为圆心,以大于AC为半径作弧,两弧交于点E,作射线BE交AC于点O,交AD于点F,O是AC的中点,AD∥BC,下列结论:①△AOF≌△COB;②AC平分∠BAD;③BC的长为3.其中正确的有( )
A.3个 B.2个 C.1个 D.0个
二、填空题(本大题共6小题,每小题3分,共18分)
11.如图9,点C是线段BD的中点,∠B=90 ,∠A=30 ,CD=2,则AC的长为 .
图9 图10 图11
12.如图10,已知点B在射线AE上,AE平分∠CAD,要使△ABC≌△ABD,需要添加的一个条件是 .
13.如图11,网格中每个小正方形的边长均为1,以A为圆心,AB为半径画弧,交最上方的网格线与点D,则以ED为边长的正方形的面积为 .
14.图12-①是一款可以伸缩的衣架,它是由四个全等的四边形组成,图12-②是它的示意图,已知AB=AD=15 cm,∠A=60 ,则点B与点M之间的距离BM= cm.
图12 图13
15.如图13,一架长为13米的云梯AB斜靠在墙上,云梯的顶端A到墙角E的距离AE=
12米,当云梯的顶端A向下滑动7米到点C处时,云梯的底端B向外滑动的距离BD=
米.
16.当题目条件出现角平分线时,我们往往可以构造等腰三角形解决问题,如图14-①,在△ABC中,∠A=2∠B,CD平分∠ACB,AD=2,AC=3,求BC的长,解决方法:如图14-②,在BC边上取点E,使EC=AC,连接DE,可得△DEC≌△DAC,且△BDE是等腰三角形,所以BC的长为5.试通过构造等腰三角形解决问题:如图14-③,在△ABC中,AB=AC,∠A=20°,BD平分∠ABC,BC=a,BD=b,CD=c,则AC的长为 .
① ② ③
图14
三、解答题(本大题共6小题,共52分)
17.(6分)如图15,在△ABC中,∠A=90 ,点D是BC边的中点,点E在AB边上,且AE=1,AB=8,AC=6,DE=4,求△DBE的周长.
图15 图16
18.(8分)如图16,在△ABC中,BD⊥AC于点D,CE平分∠ACB,交AB于点E,∠A=59 ,∠CBD=24 ,求∠ABC和∠AEC的度数.
19.(8分)如图17,在四边形ABCD中,点E,F分别在边AB,CD上,AG⊥直线EF于点G,CH⊥直线EF于点H,且AG=CH,FG=EH.
(1)试判断AB与DC的位置关系,并说明理由;
(2)若∠GAE=30 ,GE=1,求CF的长.
图17 图18
20.(8分)在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)求格点△ABC的面积;
(2)请你在图中画出与△ABC成轴对称的格点三角形(画出3个即可).
21.(10分)中国古代数学家们对于勾股定理的发现和验证,在世界数学史上具有独特的发现和地位.现由4个全等的直角三角形构成了如图19所示的“弦图”,在Rt△ABC中,AC=b,BC=a,AB=c,请你利用这个图形解答下列问题:
(1)试说明:a2+b2=c2;
(2)如果大正方形的面积为10,小正方形的面积为2,求(a+b)2的值.
图19 图20
22.(12分)如图20,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:(1)如果把以上问题中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?说明理由.
(2)如果把以上问题中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
附加题(20分,不计入总分)
23.综合与探究:
如图21,在Rt△ABC中,∠B=90 ,AB=8 cm,AC=10 cm,动点P从点A出发,沿着A→B的方向运动,且速度为cm/s,动点Q从B出发,沿着B→C→A的方向运动,且速度为每秒1 cm/s,它们同时出发,设出发的时间为t s.
(1)当t=4 s时,求△PBQ的面积;
(2)点P在边AB上运动的过程中,若点P正好落在斜边AC的垂直平分线上,求此时t的值,并求出此时CQ的长;
(3)若点Q在斜边AC上运动过程中,是否存在t的值,使得△BCQ恰好是等腰三角形,若存在,求出所有t的值;若不存在,请说明理由.
图21
期中达标测试卷参考答案:
一、1.C 2.C 3.A 4.B 5.D 6.C 7.B 8.A 9.A 10.B
二、11.4 12.答案不唯一,如AC=AD 13.5 14.60 15.7
16.a+b+c 提示:如图1所示,因为△ABC中,AB=AC,∠A=20°,所以∠ABC=
∠C=80°.因为BD平分∠ABC,所以∠1=∠2=40°,∠BDC=60°.在BA边上取点E,使BE=BC=a,连接DE,易得△DBE≌△DBC(SAS).所以∠BED=∠C=80°.所以∠4=
60°.所以∠3=60°.在DA边上取点F,使DF=DB,连接FE,易得△BDE≌△FDE(SAS).所以∠5=∠1=40°,FE=BE= a.因为∠A=20°,所以∠6=20°,所以AF=EF=a.因为DF=BD= b,所以AC=AF+DF+CD=a+b+c.
图1
三、17.解:在Rt△ABC中,由勾股定理,得BC2=AB2+AC2=82+62=100.因为点D是BC边的中点,所以BD=BC=5.因为AE=1,所以BE=8-1=7,所以△DBE的周长=BE+
BD+DE=7+5+4=16.
18.解:因为BD⊥AC,所以∠ADB=90 .因为∠A=59 ,所以∠ABD=90 -59 =31 .所以∠ABC=∠ABD+∠CBD=31 +24 =55 .所以∠ACB=90 -∠CBD=90 -24 =66 .因为CE平分∠ACB,所以∠ACE=∠ACB=×66 =33 .所以∠AEC=180 -∠A-∠ACE=180 -59 -33 =88 .
19.解:(1)AB∥DC.理由:因为GF=EH,所以EG=FH.因为AG=CH,∠G=∠H=90 ,所以△AGE≌△CHF(SAS) .所以∠AEG=∠CFH.因为∠AEF=180 -∠AEG,∠CFE=180 -∠CFH,所以∠AEF=∠CFE,所以AB∥CD.
(2)因为∠GAE=30 ,GE=1,所以AE=2EG=2×1=2.因为△AGE≌△CHF,所以CF=AE=2.
20.解:(1)S△ABC=×2×2=2.
(2)答案不唯一,如△ABC1,△A1BC,△DEF,画出的图形如图2所示.
图2
21.解:(1)由图可知,S正方形=4×ab+(b-a)2=2ab+a2-2ab+b2=a2+b2,S正方形=c2,所以a2+b2=c2.
(2)根据题意,得c2=10,(b-a)2=2.因为a2+b2=c2,所以a2+b2=10.因为(b-a)2=2,所以b2-2ab+a2=2,所以2ab=a2+b2-2=10-2=8,所以(a+b)2=a2+b2+2ab=10+8=18.
22.解:(1)∠DAC的度数不会改变.理由如下:
因为EA=EC,所以∠CAE=∠C.所以∠AEB=2∠C.因为BA=BD,所以∠BAD=(180°-∠B)=[180°-(90°-∠AEB)]=[180°-(90°-2∠C)]=45°+∠C,所以∠DAE=90°-∠BAD=90°-(45°+∠C)=45°-∠C.所以∠DAC=∠DAE+∠CAE=∠DAE+∠C=45°.
(2)设∠ABC=m°,则∠BAD=(180°-m°)=90°-m°,∠AEB=180°-n°-m°,所以∠DAE=∠BAE-∠BAD=n°-90°+m°.
因为EA=EC,所以∠CAE=∠AEB=90°-n°-m°,所以∠DAC=∠DAE+∠CAE=n°-90°+m°+90°-n°-m°=n°.
23.解:在Rt△ABC中,BC2=AC2-AB2=102-82=36,所以BC=6 cm.
(1)当t=4 s时,BP=AB-AP=8-4×=6 cm,BQ=4×1=4 cm,所以△PBQ的面积为×6×4=
12(cm2).
(2)因为点P正好落在斜边AC的垂直平分线上,所以PA=PC.因为PA=t,所以PC=
t,所以BP=8-t.所以在Rt△BPC中,由勾股定理,得BC2+BP2=PC2,所以62+(8-
t)2=(t)2,解得t=s.此时CQ=.
(3)存在.理由如下:分三种情况讨论:
①如图3-①,当CQ=BQ时,∠C=∠CBQ.因为∠A+∠C=90 ,∠CBQ+∠ABQ=90 ,所以∠A=∠ABQ,所以AQ=BQ.所以AQ=CQ.所以CQ= cm,所以BC+CQ=6+5=11 cm,所以t=11÷1=11.
① ②
图3
②当CQ=BC时,BC+CQ=6+6=12 cm,所以t=12÷1=12.
③如图3-②,当BC=BQ时,因为BC=6,所以BQ=6,过点B作BE⊥CQ,垂足为E.所以CQ=2CE.因为S△ABC=,所以8×6=10×BE,所以BE=.在Rt△BCE中,由勾股定理,得BC2=CE2+BE2,所以CE2=62-(.所以BC+CQ=6+2×=,所以t=.
综上所述,存在t的值为11或12或,使得△BCQ恰好是等腰三角形.
3 cm
6 cm
A
D
C
B
A
F
E
D
C
B
M
①
②
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
