第八章 重力势能基础巩固拓展练习(word版含答案)
文档属性
| 名称 | 第八章 重力势能基础巩固拓展练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 469.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-15 00:00:00 | ||
图片预览




文档简介
2019人教版必修第二册 第八章 2 重力势能 基础巩固 拓展练习
一、单选题
1.关于重力势能,下列说法中正确的是()
A.重力势能仅由重物本身的因素决定 B.重力势能有负值,故重力势能是矢量
C.重力不做功,物体就不具有重力势能 D.重力做功时必定引起重力势能的变化
2.奥运会蹦床比赛,运动员从空中落下,到随蹦床运动到最低点的过程中,下列说法中正确的是( )
A.动能一直增加,势能一直减小
B.动能先增加后减小,势能先减小后增加,但能量守恒
C.动能先增加后减小,势能一直减小,能量总量逐渐减小
D.运动员与蹦床接触时,动能最大
3.如图所示,在弹性限度内,将压缩量为x的弹簧缓慢拉伸至伸长量为x,关于这一过程中弹簧的弹性势能变化,下列说法正确的是( )
A.一直减小
B.一直增大
C.先减小再增大
D.先增大再减小
4.已知弹簧的劲度系数为 500N/m,在其下端竖直悬挂质量 m=20kg的重物,重物静止时,弹簧伸长
A.1m B.0.8m C.0.4m D.0.2m
5.用木板搭成斜面从卡车上卸下货物,斜面与地面夹角有两种情况,如图所示。同一货物分别从斜面顶端无初速度释放下滑到地面。已知货物与每个斜面间的动摩擦因数均相同,不计空气阻力。则货物( )
A.沿倾角α的斜面下滑到地面时机械能的损失多
B.沿倾角α的斜面下滑到地面时重力势能减小得多
C.沿两个斜面下滑过程中重力的平均功率相等
D.沿两个斜面下滑过程中所用时间相等
6.汽车爬坡时速度逐渐减小,此过程中汽车的
A.动能减小,重力势能增大 B.动能减小,重力势能减小
C.动能增大,重力势能增大 D.动能增大,重力势能减小
7.跳伞运动员在刚跳离飞机、其降落伞尚未打开的一段时间内,运动员在空中运动时受到的空气阻力不能忽略,下列说法中正确的是
A.空气阻力做正功 B.空气阻力不做功
C.重力势能增加 D.动能增加
8.如图所示,两同学站在悬崖边上,以相同的初速率从悬崖边抛出质量相同的甲、乙两球,甲球被竖直向上抛出,乙球被水平抛出,最终两球均落在悬崖下方的水面上。不计空气阻力。用、分别表示甲、乙两球从抛出到落到水面重力所做的功,用、分别表示甲、乙两球从抛出到落到水面重力势能的变化。下列说法正确的是( )
A. B. C. D.
9.“打羽毛球”是一种常见的体育健身活动.当羽毛球以的水平速度飞来时,运动员迅速挥拍以的水平速度迎面击球,假设羽毛球和羽毛球拍的碰撞为弹性碰撞,且球拍的质量远大于球的质量,羽毛球反弹的速度大小为
A. B.
C. D.
10.将一支圆珠笔倒立在桌面上,向下按压圆珠笔使笔尖露出的过程中,笔帽内弹簧的弹性势能( )
A.减小 B.增大 C.先减小后增大 D.先增大后减小
11.一蹦极运动员身系弹性蹦极绳从水面上方的高台下落,到最低点时距水面还有数米距离。假定空气阻力可忽略,运动员可视为质点,下列说法错误的是( )
A.运动员到达最低点前重力势能始终减小
B.蹦极绳张紧后的下落过程中,弹性力做负功,弹性势能增加
C.蹦极过程中,运动员、地球和蹦极绳所组成的系统机械能守恒
D.蹦极过程中,重力势能的改变量与重力势能零点的选取有关
12.将物体以某一初速度从地面竖直向上抛出,该物体上升的最大高度是h,已知物体的质量为m,所受的空气阻力大小恒为f,当地的重力加速度为则从物体被抛出到落回地面的全过程中
A.重力所做的功为2 mgh
B.空气阻力所做的功为零
C.空气阻力所做的功为
D.物体在上升过程中机械能守恒
13.如图所示,小明玩蹦蹦杆,在小明将蹦蹦杆中的弹簧向下压缩的过程中,小明的重力势能、弹簧的弹性势能的变化是( )
A.重力势能减少,弹性势能增大 B.重力势能增大,弹性势能减少
C.重力势能减少,弹性势能减少 D.重力势能不变,弹性势能增大
14.以一定初速度竖直上抛出一个质量为m的小球,小球上升的最大高度为h,空气阻力的大小为f,则从抛出点到返回至原出发点的过程中,下列说法中正确的是( )
A.空气阻力对小球做的功为零,重力对小球做的功也为零
B.空气阻力对小球做的功为零,重力对小球做的功为
C.空气阻力对小球做的功为,重力对小球做的功也为零
D.空气阻力对小球做的功为,重力对小球做的功为
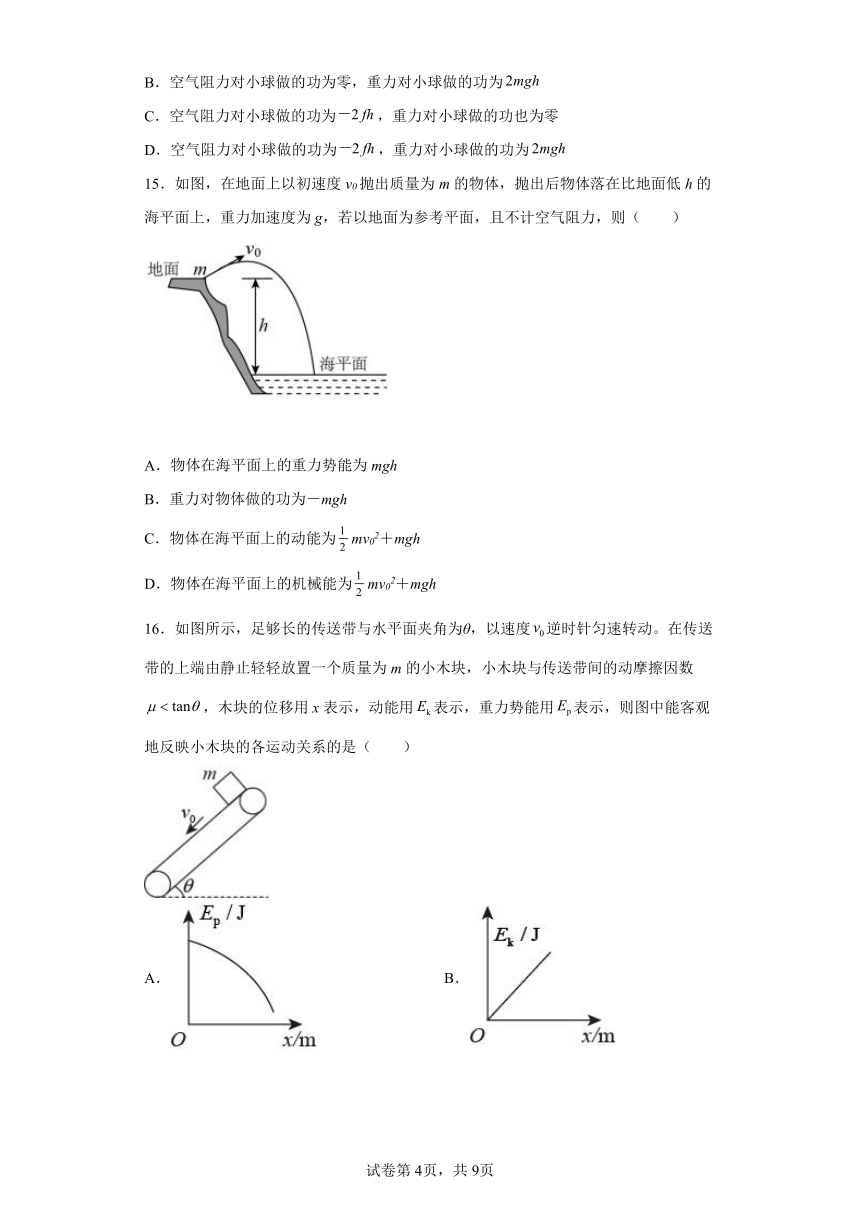
15.如图,在地面上以初速度v0抛出质量为m的物体,抛出后物体落在比地面低h的海平面上,重力加速度为g,若以地面为参考平面,且不计空气阻力,则( )
A.物体在海平面上的重力势能为mgh
B.重力对物体做的功为-mgh
C.物体在海平面上的动能为mv02+mgh
D.物体在海平面上的机械能为mv02+mgh
16.如图所示,足够长的传送带与水平面夹角为θ,以速度逆时针匀速转动。在传送带的上端由静止轻轻放置一个质量为m的小木块,小木块与传送带间的动摩擦因数,木块的位移用x表示,动能用表示,重力势能用表示,则图中能客观地反映小木块的各运动关系的是( )
A. B.
C. D.
17.某实验室工作人员,用初速度v0=0.09c(c为真空中的光速)的α粒子轰击静止的氮原子核,生产了质子,若某次碰撞可看作对心正碰,碰后新核与质子同方向运动,垂直磁场方向射入磁场,通过分析偏转半径可得出新核与质子的速度大小之比为1:20,已知质子的质量为m( )
A.该核反应方程
B.质子的速度v为0.20c
C.若用两个上述质子发生对心弹性碰撞,则每个质子的动量变化量是0.20mc
D.若用两个上述质子发生对心弹性碰撞,则每个质子的动量变化量方向与末动量方向相反
18.如图所示,货物放在自动扶梯的水平台阶上,随扶梯一起向斜上方做匀速直线运动,下列说法正确的是
A.重力对货物做正功
B.摩擦力对货物做正功
C.支持力对货物做正功
D.合外力对货物做正功
19.关于弹性势能和重力势能,下列说法中正确的是( )
A.弹簧的弹性势能大小只与弹簧的材料有关
B.在弹性限度内,弹簧的弹性势能大小与弹簧形变量有关
C.重力势能的变化量与参考平面的选取有关
D.当重力对物体做正功时,物体的重力势能一定增加
20.如图所示,一根轻质弹簧左端固定,现使滑块沿光滑水平桌面滑向弹簧,在滑块接触到弹簧直到速度减为零的过程中,弹簧的( )
A.弹力越来越大,弹性势能越来越大
B.弹力越来越小,弹性势能越来越小
C.弹力先变小后变大,弹性势能越来越小
D.弹力先变大后变小,弹性势能越来越大
二、多选题
21.与物体的重力势能有关的因素是()
A.物体的质量 B.物体的速度 C.物体和参考平面之间的高度差 D.物体的大小
22.应用物理知识分析生活中的常见现象,可以使物理学习更加有趣和深入.例如你用手掌平托一苹果(可视为质点),保持这样的姿势让苹果在竖直平面内以速率v沿顺时针方向做半径为R的匀速圆周运动.假设t=0时刻苹果在最低点a且重力势能为零,则在苹果从最低点a运动到最高点c的过程中,下列说法正确的是( )
A.苹果的合力不为零
B.苹果的加速度越来越小
C.手对苹果的作用力做正功
D.苹果的重力势能随时间的变化关系为Ep=mgRcos
23.如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h.圆环在C处获得竖直向上的速度,恰好能回到A处.弹簧始终在弹性限度内,重力加速度为g.则圆环
A.下滑过程中,加速度一直减小
B.上滑过程中,经过B处的速度最大
C.下滑过程中,克服摩擦力做的功为mv2
D.上滑经过B的速度大于下滑经过B的速度
三、解答题
24.如图,质量m=20kg的小朋友从滑梯A点由静止下滑,已知A点距地面高h=1.8m,取g=10m/s2。(小朋友可视为质点,不计一切摩擦)
(1)选择地面为参考平面,在A点时,他的重力势能为多少?
(2)滑到滑梯末端B时,他的速度大小为多少?
25.所谓“深空探测”是指航天器脱离地球引力场,进入太阳系空间或更远的宇宙空间进行探测,现在世界范围内的深空探测主要包括对月球、金星、火星、木星等太阳系星体的探测.继对月球进行深空探测后,2018年左右我国将进行第一次火星探测.图示为探测器在火星上着陆最后阶段的模拟示意图.首先在发动机作用下,探测器受到推力作用在距火星表面一定高度处(远小于火星半径)悬停;此后发动机突然关闭,探测器仅受重力下落2t0时间(未着地),然后重新开启发动机使探测器匀减速下降,经过时间t0,速度为0时探测器恰好到达火星表面.已知探测器总质量为m(不计燃料燃烧引起的质量变化),地球和火星的半径的比值为k1,质量的比值为k2,地球表面附近的重力加速度为g,求:
(1)探测器悬停时发动机对探测器施加的力.
(2)探测器悬停时具有的重力势能(火星表面为零势能面).
26.质量为50kg的人沿着长、倾角为的坡路走上一个土丘,重力对他所做的功是多少?他克服重力所做的功是多少?他的重力势能增加了多少?
27.蹦床比赛分成预备运动和比赛动作.最初,运动员静止站在蹦床上在预备运动阶段,他经过若干次蹦跳,逐渐增加上升高度,最终达到完成比赛动作所需的高度;此后,进入比赛动作阶段.
把蹦床简化为一个竖直放置的轻弹簧,弹力大小F=kx (x为床面下沉的距离,k为常量).质量m=50kg的运动员静止站在蹦床上,床面下沉x0=0.10m;在预备运动中,假设运动员所做的总功W全部用于其机械能;在比赛动作中,把该运动员视作质点,其每次离开床面做竖直上抛运动的腾空时间均为△t=2.0s,设运动员每次落下使床面压缩的最大深度均为xl.取重力加速度g=10m/s2,忽略空气阻力的影响.
(1)求常量k,并在图中画出弹力F随x变化的示意图;
(2)求在比赛动作中,运动员离开床面后上升的最大高度hm;
(3)借助F-x 图像可以确定弹性做功的规律,在此基础上,求 x1和W的值
28.如图所示,长为1.8m的轻质细线一端固定于O点,另一端系一质量m=0.5kg的小球。把小球拉到A点由静止释放,O、A在同一水平面上,B为小球运动的最低点。忽略空气阻力,取B点的重力势能为零,重力加速度g=10m/s2,求:
(1)小球受到重力的大小;
(2)小球在A点的重力势能;
(3)小球运动到B点时速度的大小。
29.质量m=3kg的物体,在水平力F=6N的作用下,在光滑的水平面上从静止开始运动,运动时间t=3s,求:
(1)力F在t=3s内对物体所做的功;
(2)力F在t=3s内对物体所做功的平均功率。
30.世界著名撑杆跳高运动员乌克兰名将布勃卡身高1.83 m,体重80 kg,他曾多次打破撑杆跳高的世界纪录,目前仍保持着6.14 m的室外世界纪录.请你探究以下两个问题(g取10 m/s2):
(1)他跳过6.14 m时,至少克服重力做多少功?
(2)他的重力势能改变了多少?
31.在水平地面上铺n块砖,每块砖的质量均为m,厚度均为h,如图所示。现将砖一块一块地竖直叠放起来,砖的重力势能增加多少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【详解】
重力势能与参考面的选取有关,由重物的质量和高度决定,故A错误;重力势能是标量,其负值表示物体位于零势面的下方,故B错误;重力势能与参考面的选取有关,重力做功时重力势能发生改变,但不做功时物体也可能具有重力势能,故C错误;由功能关系可知,重力做功引起重力势能的变化,故D正确.
2.B
【解析】
【详解】
运动员从空中落下到落到蹦床上的过程中,动能增加,势能减小;落到蹦床上后开始时运动员由于受重力大于弹力而先加速,当弹力等于重力时,加速度为零,速度最大,动能最大;以后由于弹力大于重力而做减速运动到最低点时速度为零,则整个过程中动能先增加后减小;由于总能量守恒,则重力势能和弹性势能之和先减小后增加,综上所述,选项B正确,ACD错误;故选B.
【点睛】
此题关键是能分析人落到蹦床上时受力的情况,从而讨论速度及动能的变化;知道能量守恒关系以及能量的转化情况.
3.C
【解析】
【分析】
【详解】
因为弹簧刚开始是被压缩的,恢复原长之前,在拉伸过程中形变量变小,根据公式可得弹性势能减小,在恢复形变量之后,在拉伸过程中形变量变大,根据公式弹性势能增大,故先减小后增大。
故选C。
4.C
【解析】
【详解】
根据平衡条件得知,物体受到的弹力大小等于物体的重力大小,即为:F=mg=200N;由胡克定律F=kx得弹簧伸长的长度为:,故C正确,ABD错误.
5.A
【解析】
【详解】
A.设斜面长为,货物距地面的高度为,根据功的定义式可知,滑动摩擦力对货物做的功为
所以货物与斜面动摩擦因数一定时,倾角越小,克服摩擦力做功越多,机械能损失越多,故A正确;
B.下滑到地面时的高度相同,重力做功相同,重力势能减少量相同,故B错误;
CD.根据
沿倾角大的斜面下滑时货物的加速度大,根据
可知,沿倾角大的斜面下滑时所用时间短,根据
可知沿斜面下滑过程中重力的功率大,故CD错误;
故选A。
6.A
【解析】
【详解】
汽车爬坡时速度逐渐减小,由Ek=mv2,则动能减小,根据EP=mgh可知,随高度的增加重力势能变大;
A.动能减小,重力势能增大,与结论相符,选项A正确;
B.动能减小,重力势能减小,与结论不相符,选项B错误;
C.动能增大,重力势能增大,与结论不相符,选项C错误;
D.动能增大,重力势能减小,与结论不相符,选项D错误;
7.D
【解析】
【详解】
运动员下降时,受到空气阻力作用,阻力向上,运动员向下,阻力对运动员做负功.选项AB错误;运动员下降时,质量不变,高度不断减小,重力做正功,重力势能逐渐减小.故C错误.运动员下降时,质量不变,速度不断增大,动能不断增大.故D正确.
8.A
【解析】
【分析】
【详解】
AB.根据重力做功特点,重力做功只与初末位置有关,可知
故A正确,B错误;
CD.重力势能的变化只与相对高度有关,所以
故CD错误。
故选A。
9.A
【解析】
【详解】
设碰撞前羽毛球和羽毛球拍的速度分别为v1和v2,碰后羽毛球和羽毛球拍的速度分别为 和 .取碰撞前羽毛球的速度方向为正方向,根据动量守恒定律和机械能守恒定律得:,.联立得 ,据题有得.故A正确.
10.B
【解析】
【详解】
向下按压圆珠笔使笔尖露出的过程,弹簧的形变逐渐增大,则笔帽内弹簧的弹性势能增大,故选B。
11.D
【解析】
【详解】
A.运动员到达最低点前重力始终做正功,重力势能始终减小,故A正确,不符合题意;
B.蹦极绳张紧后的下落过程中,弹力方向与位移方向始终相反,弹力做负功,弹性势能增加,故B正确,不符合题意;
C.以运动员、地球和蹦极绳所组成的系统,只有重力和弹力做功,则系统的机械能守恒,故C正确,不符合题意;
D.重力势能的改变与重力做功有关,取决于初末位置的高度差,与重力势能零点的选取无关,故D错误,符合题意。
故选D。
12.C
【解析】
【详解】
A项:回到出发点,物体整个运动过程中始末位置相同,故重力做功为0,所以A错误;
B、C项:上升和下降过程中阻力始终做负功,所以克服阻力做功为2fh,故B错误,C正确;
D项:由于上升过程中阻力做负功,所以物体的机械能减小,故D错误.
13.A
【解析】
【详解】
弹簧向下压缩的过程中,弹簧压缩量增大,弹性势能增加;下降中,重力做正功,重力势能减少。故A正确,BCD错误。
故选A。
14.C
【解析】
【分析】
将小球的运动过程分为上升和下落两个过程研究:上升过程空气阻力做负功.下落过程空气阻力也做负功,整个过程空气阻力对小球做功是两个过程之和.
【详解】
从抛出点至落回到原出发点的过程中,由于初末位置重合,所以重力对小球做功为零.上升过程:空气阻力对小球做功为:,下落过程:空气阻力对小球做功为:,则从抛出到落回到抛出点的过程中,空气阻力对小球做的功为:,故选C.
【点睛】
对功的公式要加深理解,不同的力做功l的含义不同,对于滑动摩擦力、空气阻力做功l是路程.重力做功与初末位置有关,而摩擦力做功与路径有关.
15.C
【解析】
【分析】
【详解】
A.以地面为参考平面,海平面低于地面的高度为h,所以物体在海平面上时的重力势能为-mgh,故A错误;
B.重力做功与路径无关,与初、末位置的高度差有关,抛出点与海平面的高度差为h,并且重力做正功,所以整个过程重力对物体做功为mgh,故B错误;
C.由动能定理得
mgh=Ek2-mv02
则物体在海平面上的动能为
Ek2=mv02+mgh
故C正确;
D.根据机械能守恒知,物体在海平面上的机械能等于抛出时的机械能,为
E=mv02
故D错误。
故选C。
16.C
【解析】
【详解】
初状态时:重力的分力与摩擦力均沿着斜面向下,且都是恒力,所以物体先沿斜面做匀加速直线运动,由牛顿第二定律可得加速度
当小木块的速度与传送带速度相等时,由于知木块与传送带不能一起匀速下滑,要继续加速运动
A.以地面为零势能面,设传送带长度为l,则有
A错误;
BC.根据动能定理得,共速前
为共速时的位移,共速后
B错误,C正确;
D.共速前,根据位移公式得
为共速时的时间,共速后
D错误。
故选C。
17.B
【解析】
【分析】
【详解】
A.新原子核的质量数
核电荷数
核反应方程
故A错误;
B.α粒子、新核的质量分别为4m、17m,质子的速度为v,由题意可知新核的速度为,由于是对心正碰,选取α粒子运动的方向为正方向,则由动量守恒得
解得
故B正确;
CD.两质子质量相等且发生对心弹性碰撞,则碰撞后两质子交换速度;对某一质子,选其末动量方向为正方向,则
又
故解出
方向与末动量方向一致,故CD错误。
故选B。
18.C
【解析】
【详解】
对货物受力分析,受到重力和水平台阶对货物竖直向上的支持力,由于随扶梯一起向斜上方做匀速直线运动,根据平衡条件可得水平台阶对货物没有摩擦力,合外力为零,所以重力对货物做负功,支持力对货物做正功,合外力对货物做不做功,故选项C正确,A、B、D错误.
19.B
【解析】
【分析】
【详解】
AB.弹簧的弹性势能大小不仅与弹簧的材料有关,还与弹簧的形变量有关,A错误,B正确;
C.重力势能的变化量与参考平面的选取无关,C错误;
D.当重力对物体做正功时,物体的重力势能一定减小,D错误。
故选B。
20.A
【解析】
【详解】
滑块接触到弹簧直到速度减为零的过程中,弹簧形变量越来越大,根据
知弹力越来越大。滑块接触到弹簧直到速度减为零的过程中,弹簧弹力一直做负功,物块的动能逐渐转化为弹簧的弹性势能,弹簧的弹性势能越来越大。
故选A。
21.AC
【解析】
【详解】
物体重力势能的表达式:,由物体的重力和物体距参考平面的高度决定,AC正确,BD错误;
故选AC.
22.AC
【解析】
【详解】
AB、在苹果从最低点a运动到最高点c的过程中,苹果做匀速圆周运动,加速度大小不变,合力不为零,故A正确,B错误;
C、在苹果从最低点a运动到最高点c的过程中,动能不变,重力势能增大,苹果的机械能增加,所以手对苹果的作用力做正功,故C正确;
D、苹果的上升的高度为,苹果的重力势能随时间的变化关系为,故D错误;
故选AC.
23.CD
【解析】
【详解】
A.圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,所以圆环先做加速运动,再做减速运动,经过B处的速度最大,所以经过B处的加速度为零,所以加速度先减小,后增大,故A错误;
BD.从A到B
从C到A
联立解得
所以B错误,D正确;
C.从A到C,根据能量守恒
从C到A
联立解得
故C正确.
故选CD。
点睛:本题涉及到受力分析、运动过程、能量变化的分析,由运动分析,由经过B处的速度最,得到加速度等于零,因数物体是在变力作用下的非匀变速直线运动,故一定是利用能的观点解决问题,即由能量守恒得到摩擦力做功和弹性势能的大小.
24.(1)360J;(2)6m/s
【解析】
【详解】
(1)选择地面为参考平面,在A点时,他的重力势能为
(2)从A到B,由机械能守恒定律可知
解得
25.(1) (2)
【解析】
【详解】
本题考查万有引力定律与牛顿运动定律和运动学公式相结合.需运用万有引力等于星球表面物体所受重力、牛顿第二定律、运动学公式等知识求解.
(1)设地球的质量和半径分别为M和R,火星的质量、半径和表面重力加速度分别为M'、R'和g'
根据万有引力等于重力有:
和
联立解得:
探测器悬停时,根据力的平衡可知,发动机对探测器施加的力
(2)设重新开启发动机时探测器速度为v,则
,
所以探测器悬停时距火星表面高度
解得:
探测器悬停时具有的重力势能
26.-37500J,37500J,37500J
【解析】
【分析】
【详解】
重力对他做功为
W=-mgh=-50×10×150×sin30°=-37500J
他克服重力做功为
W=mgh=50×10×150 ×sin30°=37500J
由
W G=-△E P
可知重力势能增加37500J。
27.(1)5000N/m ;(2)5m;(3)1.1m;2525J
【解析】
【分析】
【详解】
(1)床面下沉x0=0.1m时,运动员受力平衡,有
mg=kx0
解得
k=5×103N/m.
F-x图线如图所示.
(2)运动员从x=0处离开床面,开始腾空,由运动的对称性知其上升、下落的时间相等,
解得
hm=5.0m
(3)参照由速度时间图线求位移的方法可知F-x图线下的面积等于弹力做的功,从x处到x=0处,弹力做的功
运动员从x1处上升到最大高度hm的过程,根据动能定理可得
解得
x1=1.1m
对整个预备运动过程分析,由题设条件以及功和能的关系,有
解得
W=2525J.
28.(1)5N;(2)9J;(3)6m/s
【解析】
【详解】
(1)小球受到重力的大小
(2)取B点的重力势能为零,则小球在A点重力势能
(3)小球由A摆至B过程,由动能定理可得
解得小球到B点速度
29.(1)54J;(2)18W
【解析】
【详解】
(1)根据牛顿第二定律可求出加速度
则物体在3s末的速度
物体在3s内的位移
力F做的功
(2)力F在3s内的平均功率
30.(1)4180J (2)增加了4180J
【解析】
【详解】
(1)运动员跳过6.14m,其重心至少升高6.14m高度处.该运动员升高1.83m,重心的高度约为0.915m,故跳过6.14m的高度,至少克服重力做功:
;
(2)运动员跳到6.14m高度处过程中,其重力做负功,所以运动员的重力势能增加,克服重力做的功就等于重力势能的增加量,所以重力势能增加了4180J.
31.n(n-1)mgh
【解析】
【分析】
【详解】
取n块砖的整体为研究对象,平放时重心的高度
h1=
选取地面为参考平面,其相应的重力势能为
Ep1=
n块砖被竖直叠放后的重心高度
h2=
其相应的重力势能为
Ep2=nmg·=
故
ΔEp=Ep2-Ep1=-=n(n-1)mgh
答案第1页,共2页
答案第1页,共2页
一、单选题
1.关于重力势能,下列说法中正确的是()
A.重力势能仅由重物本身的因素决定 B.重力势能有负值,故重力势能是矢量
C.重力不做功,物体就不具有重力势能 D.重力做功时必定引起重力势能的变化
2.奥运会蹦床比赛,运动员从空中落下,到随蹦床运动到最低点的过程中,下列说法中正确的是( )
A.动能一直增加,势能一直减小
B.动能先增加后减小,势能先减小后增加,但能量守恒
C.动能先增加后减小,势能一直减小,能量总量逐渐减小
D.运动员与蹦床接触时,动能最大
3.如图所示,在弹性限度内,将压缩量为x的弹簧缓慢拉伸至伸长量为x,关于这一过程中弹簧的弹性势能变化,下列说法正确的是( )
A.一直减小
B.一直增大
C.先减小再增大
D.先增大再减小
4.已知弹簧的劲度系数为 500N/m,在其下端竖直悬挂质量 m=20kg的重物,重物静止时,弹簧伸长
A.1m B.0.8m C.0.4m D.0.2m
5.用木板搭成斜面从卡车上卸下货物,斜面与地面夹角有两种情况,如图所示。同一货物分别从斜面顶端无初速度释放下滑到地面。已知货物与每个斜面间的动摩擦因数均相同,不计空气阻力。则货物( )
A.沿倾角α的斜面下滑到地面时机械能的损失多
B.沿倾角α的斜面下滑到地面时重力势能减小得多
C.沿两个斜面下滑过程中重力的平均功率相等
D.沿两个斜面下滑过程中所用时间相等
6.汽车爬坡时速度逐渐减小,此过程中汽车的
A.动能减小,重力势能增大 B.动能减小,重力势能减小
C.动能增大,重力势能增大 D.动能增大,重力势能减小
7.跳伞运动员在刚跳离飞机、其降落伞尚未打开的一段时间内,运动员在空中运动时受到的空气阻力不能忽略,下列说法中正确的是
A.空气阻力做正功 B.空气阻力不做功
C.重力势能增加 D.动能增加
8.如图所示,两同学站在悬崖边上,以相同的初速率从悬崖边抛出质量相同的甲、乙两球,甲球被竖直向上抛出,乙球被水平抛出,最终两球均落在悬崖下方的水面上。不计空气阻力。用、分别表示甲、乙两球从抛出到落到水面重力所做的功,用、分别表示甲、乙两球从抛出到落到水面重力势能的变化。下列说法正确的是( )
A. B. C. D.
9.“打羽毛球”是一种常见的体育健身活动.当羽毛球以的水平速度飞来时,运动员迅速挥拍以的水平速度迎面击球,假设羽毛球和羽毛球拍的碰撞为弹性碰撞,且球拍的质量远大于球的质量,羽毛球反弹的速度大小为
A. B.
C. D.
10.将一支圆珠笔倒立在桌面上,向下按压圆珠笔使笔尖露出的过程中,笔帽内弹簧的弹性势能( )
A.减小 B.增大 C.先减小后增大 D.先增大后减小
11.一蹦极运动员身系弹性蹦极绳从水面上方的高台下落,到最低点时距水面还有数米距离。假定空气阻力可忽略,运动员可视为质点,下列说法错误的是( )
A.运动员到达最低点前重力势能始终减小
B.蹦极绳张紧后的下落过程中,弹性力做负功,弹性势能增加
C.蹦极过程中,运动员、地球和蹦极绳所组成的系统机械能守恒
D.蹦极过程中,重力势能的改变量与重力势能零点的选取有关
12.将物体以某一初速度从地面竖直向上抛出,该物体上升的最大高度是h,已知物体的质量为m,所受的空气阻力大小恒为f,当地的重力加速度为则从物体被抛出到落回地面的全过程中
A.重力所做的功为2 mgh
B.空气阻力所做的功为零
C.空气阻力所做的功为
D.物体在上升过程中机械能守恒
13.如图所示,小明玩蹦蹦杆,在小明将蹦蹦杆中的弹簧向下压缩的过程中,小明的重力势能、弹簧的弹性势能的变化是( )
A.重力势能减少,弹性势能增大 B.重力势能增大,弹性势能减少
C.重力势能减少,弹性势能减少 D.重力势能不变,弹性势能增大
14.以一定初速度竖直上抛出一个质量为m的小球,小球上升的最大高度为h,空气阻力的大小为f,则从抛出点到返回至原出发点的过程中,下列说法中正确的是( )
A.空气阻力对小球做的功为零,重力对小球做的功也为零
B.空气阻力对小球做的功为零,重力对小球做的功为
C.空气阻力对小球做的功为,重力对小球做的功也为零
D.空气阻力对小球做的功为,重力对小球做的功为
15.如图,在地面上以初速度v0抛出质量为m的物体,抛出后物体落在比地面低h的海平面上,重力加速度为g,若以地面为参考平面,且不计空气阻力,则( )
A.物体在海平面上的重力势能为mgh
B.重力对物体做的功为-mgh
C.物体在海平面上的动能为mv02+mgh
D.物体在海平面上的机械能为mv02+mgh
16.如图所示,足够长的传送带与水平面夹角为θ,以速度逆时针匀速转动。在传送带的上端由静止轻轻放置一个质量为m的小木块,小木块与传送带间的动摩擦因数,木块的位移用x表示,动能用表示,重力势能用表示,则图中能客观地反映小木块的各运动关系的是( )
A. B.
C. D.
17.某实验室工作人员,用初速度v0=0.09c(c为真空中的光速)的α粒子轰击静止的氮原子核,生产了质子,若某次碰撞可看作对心正碰,碰后新核与质子同方向运动,垂直磁场方向射入磁场,通过分析偏转半径可得出新核与质子的速度大小之比为1:20,已知质子的质量为m( )
A.该核反应方程
B.质子的速度v为0.20c
C.若用两个上述质子发生对心弹性碰撞,则每个质子的动量变化量是0.20mc
D.若用两个上述质子发生对心弹性碰撞,则每个质子的动量变化量方向与末动量方向相反
18.如图所示,货物放在自动扶梯的水平台阶上,随扶梯一起向斜上方做匀速直线运动,下列说法正确的是
A.重力对货物做正功
B.摩擦力对货物做正功
C.支持力对货物做正功
D.合外力对货物做正功
19.关于弹性势能和重力势能,下列说法中正确的是( )
A.弹簧的弹性势能大小只与弹簧的材料有关
B.在弹性限度内,弹簧的弹性势能大小与弹簧形变量有关
C.重力势能的变化量与参考平面的选取有关
D.当重力对物体做正功时,物体的重力势能一定增加
20.如图所示,一根轻质弹簧左端固定,现使滑块沿光滑水平桌面滑向弹簧,在滑块接触到弹簧直到速度减为零的过程中,弹簧的( )
A.弹力越来越大,弹性势能越来越大
B.弹力越来越小,弹性势能越来越小
C.弹力先变小后变大,弹性势能越来越小
D.弹力先变大后变小,弹性势能越来越大
二、多选题
21.与物体的重力势能有关的因素是()
A.物体的质量 B.物体的速度 C.物体和参考平面之间的高度差 D.物体的大小
22.应用物理知识分析生活中的常见现象,可以使物理学习更加有趣和深入.例如你用手掌平托一苹果(可视为质点),保持这样的姿势让苹果在竖直平面内以速率v沿顺时针方向做半径为R的匀速圆周运动.假设t=0时刻苹果在最低点a且重力势能为零,则在苹果从最低点a运动到最高点c的过程中,下列说法正确的是( )
A.苹果的合力不为零
B.苹果的加速度越来越小
C.手对苹果的作用力做正功
D.苹果的重力势能随时间的变化关系为Ep=mgRcos
23.如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h.圆环在C处获得竖直向上的速度,恰好能回到A处.弹簧始终在弹性限度内,重力加速度为g.则圆环
A.下滑过程中,加速度一直减小
B.上滑过程中,经过B处的速度最大
C.下滑过程中,克服摩擦力做的功为mv2
D.上滑经过B的速度大于下滑经过B的速度
三、解答题
24.如图,质量m=20kg的小朋友从滑梯A点由静止下滑,已知A点距地面高h=1.8m,取g=10m/s2。(小朋友可视为质点,不计一切摩擦)
(1)选择地面为参考平面,在A点时,他的重力势能为多少?
(2)滑到滑梯末端B时,他的速度大小为多少?
25.所谓“深空探测”是指航天器脱离地球引力场,进入太阳系空间或更远的宇宙空间进行探测,现在世界范围内的深空探测主要包括对月球、金星、火星、木星等太阳系星体的探测.继对月球进行深空探测后,2018年左右我国将进行第一次火星探测.图示为探测器在火星上着陆最后阶段的模拟示意图.首先在发动机作用下,探测器受到推力作用在距火星表面一定高度处(远小于火星半径)悬停;此后发动机突然关闭,探测器仅受重力下落2t0时间(未着地),然后重新开启发动机使探测器匀减速下降,经过时间t0,速度为0时探测器恰好到达火星表面.已知探测器总质量为m(不计燃料燃烧引起的质量变化),地球和火星的半径的比值为k1,质量的比值为k2,地球表面附近的重力加速度为g,求:
(1)探测器悬停时发动机对探测器施加的力.
(2)探测器悬停时具有的重力势能(火星表面为零势能面).
26.质量为50kg的人沿着长、倾角为的坡路走上一个土丘,重力对他所做的功是多少?他克服重力所做的功是多少?他的重力势能增加了多少?
27.蹦床比赛分成预备运动和比赛动作.最初,运动员静止站在蹦床上在预备运动阶段,他经过若干次蹦跳,逐渐增加上升高度,最终达到完成比赛动作所需的高度;此后,进入比赛动作阶段.
把蹦床简化为一个竖直放置的轻弹簧,弹力大小F=kx (x为床面下沉的距离,k为常量).质量m=50kg的运动员静止站在蹦床上,床面下沉x0=0.10m;在预备运动中,假设运动员所做的总功W全部用于其机械能;在比赛动作中,把该运动员视作质点,其每次离开床面做竖直上抛运动的腾空时间均为△t=2.0s,设运动员每次落下使床面压缩的最大深度均为xl.取重力加速度g=10m/s2,忽略空气阻力的影响.
(1)求常量k,并在图中画出弹力F随x变化的示意图;
(2)求在比赛动作中,运动员离开床面后上升的最大高度hm;
(3)借助F-x 图像可以确定弹性做功的规律,在此基础上,求 x1和W的值
28.如图所示,长为1.8m的轻质细线一端固定于O点,另一端系一质量m=0.5kg的小球。把小球拉到A点由静止释放,O、A在同一水平面上,B为小球运动的最低点。忽略空气阻力,取B点的重力势能为零,重力加速度g=10m/s2,求:
(1)小球受到重力的大小;
(2)小球在A点的重力势能;
(3)小球运动到B点时速度的大小。
29.质量m=3kg的物体,在水平力F=6N的作用下,在光滑的水平面上从静止开始运动,运动时间t=3s,求:
(1)力F在t=3s内对物体所做的功;
(2)力F在t=3s内对物体所做功的平均功率。
30.世界著名撑杆跳高运动员乌克兰名将布勃卡身高1.83 m,体重80 kg,他曾多次打破撑杆跳高的世界纪录,目前仍保持着6.14 m的室外世界纪录.请你探究以下两个问题(g取10 m/s2):
(1)他跳过6.14 m时,至少克服重力做多少功?
(2)他的重力势能改变了多少?
31.在水平地面上铺n块砖,每块砖的质量均为m,厚度均为h,如图所示。现将砖一块一块地竖直叠放起来,砖的重力势能增加多少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【详解】
重力势能与参考面的选取有关,由重物的质量和高度决定,故A错误;重力势能是标量,其负值表示物体位于零势面的下方,故B错误;重力势能与参考面的选取有关,重力做功时重力势能发生改变,但不做功时物体也可能具有重力势能,故C错误;由功能关系可知,重力做功引起重力势能的变化,故D正确.
2.B
【解析】
【详解】
运动员从空中落下到落到蹦床上的过程中,动能增加,势能减小;落到蹦床上后开始时运动员由于受重力大于弹力而先加速,当弹力等于重力时,加速度为零,速度最大,动能最大;以后由于弹力大于重力而做减速运动到最低点时速度为零,则整个过程中动能先增加后减小;由于总能量守恒,则重力势能和弹性势能之和先减小后增加,综上所述,选项B正确,ACD错误;故选B.
【点睛】
此题关键是能分析人落到蹦床上时受力的情况,从而讨论速度及动能的变化;知道能量守恒关系以及能量的转化情况.
3.C
【解析】
【分析】
【详解】
因为弹簧刚开始是被压缩的,恢复原长之前,在拉伸过程中形变量变小,根据公式可得弹性势能减小,在恢复形变量之后,在拉伸过程中形变量变大,根据公式弹性势能增大,故先减小后增大。
故选C。
4.C
【解析】
【详解】
根据平衡条件得知,物体受到的弹力大小等于物体的重力大小,即为:F=mg=200N;由胡克定律F=kx得弹簧伸长的长度为:,故C正确,ABD错误.
5.A
【解析】
【详解】
A.设斜面长为,货物距地面的高度为,根据功的定义式可知,滑动摩擦力对货物做的功为
所以货物与斜面动摩擦因数一定时,倾角越小,克服摩擦力做功越多,机械能损失越多,故A正确;
B.下滑到地面时的高度相同,重力做功相同,重力势能减少量相同,故B错误;
CD.根据
沿倾角大的斜面下滑时货物的加速度大,根据
可知,沿倾角大的斜面下滑时所用时间短,根据
可知沿斜面下滑过程中重力的功率大,故CD错误;
故选A。
6.A
【解析】
【详解】
汽车爬坡时速度逐渐减小,由Ek=mv2,则动能减小,根据EP=mgh可知,随高度的增加重力势能变大;
A.动能减小,重力势能增大,与结论相符,选项A正确;
B.动能减小,重力势能减小,与结论不相符,选项B错误;
C.动能增大,重力势能增大,与结论不相符,选项C错误;
D.动能增大,重力势能减小,与结论不相符,选项D错误;
7.D
【解析】
【详解】
运动员下降时,受到空气阻力作用,阻力向上,运动员向下,阻力对运动员做负功.选项AB错误;运动员下降时,质量不变,高度不断减小,重力做正功,重力势能逐渐减小.故C错误.运动员下降时,质量不变,速度不断增大,动能不断增大.故D正确.
8.A
【解析】
【分析】
【详解】
AB.根据重力做功特点,重力做功只与初末位置有关,可知
故A正确,B错误;
CD.重力势能的变化只与相对高度有关,所以
故CD错误。
故选A。
9.A
【解析】
【详解】
设碰撞前羽毛球和羽毛球拍的速度分别为v1和v2,碰后羽毛球和羽毛球拍的速度分别为 和 .取碰撞前羽毛球的速度方向为正方向,根据动量守恒定律和机械能守恒定律得:,.联立得 ,据题有得.故A正确.
10.B
【解析】
【详解】
向下按压圆珠笔使笔尖露出的过程,弹簧的形变逐渐增大,则笔帽内弹簧的弹性势能增大,故选B。
11.D
【解析】
【详解】
A.运动员到达最低点前重力始终做正功,重力势能始终减小,故A正确,不符合题意;
B.蹦极绳张紧后的下落过程中,弹力方向与位移方向始终相反,弹力做负功,弹性势能增加,故B正确,不符合题意;
C.以运动员、地球和蹦极绳所组成的系统,只有重力和弹力做功,则系统的机械能守恒,故C正确,不符合题意;
D.重力势能的改变与重力做功有关,取决于初末位置的高度差,与重力势能零点的选取无关,故D错误,符合题意。
故选D。
12.C
【解析】
【详解】
A项:回到出发点,物体整个运动过程中始末位置相同,故重力做功为0,所以A错误;
B、C项:上升和下降过程中阻力始终做负功,所以克服阻力做功为2fh,故B错误,C正确;
D项:由于上升过程中阻力做负功,所以物体的机械能减小,故D错误.
13.A
【解析】
【详解】
弹簧向下压缩的过程中,弹簧压缩量增大,弹性势能增加;下降中,重力做正功,重力势能减少。故A正确,BCD错误。
故选A。
14.C
【解析】
【分析】
将小球的运动过程分为上升和下落两个过程研究:上升过程空气阻力做负功.下落过程空气阻力也做负功,整个过程空气阻力对小球做功是两个过程之和.
【详解】
从抛出点至落回到原出发点的过程中,由于初末位置重合,所以重力对小球做功为零.上升过程:空气阻力对小球做功为:,下落过程:空气阻力对小球做功为:,则从抛出到落回到抛出点的过程中,空气阻力对小球做的功为:,故选C.
【点睛】
对功的公式要加深理解,不同的力做功l的含义不同,对于滑动摩擦力、空气阻力做功l是路程.重力做功与初末位置有关,而摩擦力做功与路径有关.
15.C
【解析】
【分析】
【详解】
A.以地面为参考平面,海平面低于地面的高度为h,所以物体在海平面上时的重力势能为-mgh,故A错误;
B.重力做功与路径无关,与初、末位置的高度差有关,抛出点与海平面的高度差为h,并且重力做正功,所以整个过程重力对物体做功为mgh,故B错误;
C.由动能定理得
mgh=Ek2-mv02
则物体在海平面上的动能为
Ek2=mv02+mgh
故C正确;
D.根据机械能守恒知,物体在海平面上的机械能等于抛出时的机械能,为
E=mv02
故D错误。
故选C。
16.C
【解析】
【详解】
初状态时:重力的分力与摩擦力均沿着斜面向下,且都是恒力,所以物体先沿斜面做匀加速直线运动,由牛顿第二定律可得加速度
当小木块的速度与传送带速度相等时,由于知木块与传送带不能一起匀速下滑,要继续加速运动
A.以地面为零势能面,设传送带长度为l,则有
A错误;
BC.根据动能定理得,共速前
为共速时的位移,共速后
B错误,C正确;
D.共速前,根据位移公式得
为共速时的时间,共速后
D错误。
故选C。
17.B
【解析】
【分析】
【详解】
A.新原子核的质量数
核电荷数
核反应方程
故A错误;
B.α粒子、新核的质量分别为4m、17m,质子的速度为v,由题意可知新核的速度为,由于是对心正碰,选取α粒子运动的方向为正方向,则由动量守恒得
解得
故B正确;
CD.两质子质量相等且发生对心弹性碰撞,则碰撞后两质子交换速度;对某一质子,选其末动量方向为正方向,则
又
故解出
方向与末动量方向一致,故CD错误。
故选B。
18.C
【解析】
【详解】
对货物受力分析,受到重力和水平台阶对货物竖直向上的支持力,由于随扶梯一起向斜上方做匀速直线运动,根据平衡条件可得水平台阶对货物没有摩擦力,合外力为零,所以重力对货物做负功,支持力对货物做正功,合外力对货物做不做功,故选项C正确,A、B、D错误.
19.B
【解析】
【分析】
【详解】
AB.弹簧的弹性势能大小不仅与弹簧的材料有关,还与弹簧的形变量有关,A错误,B正确;
C.重力势能的变化量与参考平面的选取无关,C错误;
D.当重力对物体做正功时,物体的重力势能一定减小,D错误。
故选B。
20.A
【解析】
【详解】
滑块接触到弹簧直到速度减为零的过程中,弹簧形变量越来越大,根据
知弹力越来越大。滑块接触到弹簧直到速度减为零的过程中,弹簧弹力一直做负功,物块的动能逐渐转化为弹簧的弹性势能,弹簧的弹性势能越来越大。
故选A。
21.AC
【解析】
【详解】
物体重力势能的表达式:,由物体的重力和物体距参考平面的高度决定,AC正确,BD错误;
故选AC.
22.AC
【解析】
【详解】
AB、在苹果从最低点a运动到最高点c的过程中,苹果做匀速圆周运动,加速度大小不变,合力不为零,故A正确,B错误;
C、在苹果从最低点a运动到最高点c的过程中,动能不变,重力势能增大,苹果的机械能增加,所以手对苹果的作用力做正功,故C正确;
D、苹果的上升的高度为,苹果的重力势能随时间的变化关系为,故D错误;
故选AC.
23.CD
【解析】
【详解】
A.圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,所以圆环先做加速运动,再做减速运动,经过B处的速度最大,所以经过B处的加速度为零,所以加速度先减小,后增大,故A错误;
BD.从A到B
从C到A
联立解得
所以B错误,D正确;
C.从A到C,根据能量守恒
从C到A
联立解得
故C正确.
故选CD。
点睛:本题涉及到受力分析、运动过程、能量变化的分析,由运动分析,由经过B处的速度最,得到加速度等于零,因数物体是在变力作用下的非匀变速直线运动,故一定是利用能的观点解决问题,即由能量守恒得到摩擦力做功和弹性势能的大小.
24.(1)360J;(2)6m/s
【解析】
【详解】
(1)选择地面为参考平面,在A点时,他的重力势能为
(2)从A到B,由机械能守恒定律可知
解得
25.(1) (2)
【解析】
【详解】
本题考查万有引力定律与牛顿运动定律和运动学公式相结合.需运用万有引力等于星球表面物体所受重力、牛顿第二定律、运动学公式等知识求解.
(1)设地球的质量和半径分别为M和R,火星的质量、半径和表面重力加速度分别为M'、R'和g'
根据万有引力等于重力有:
和
联立解得:
探测器悬停时,根据力的平衡可知,发动机对探测器施加的力
(2)设重新开启发动机时探测器速度为v,则
,
所以探测器悬停时距火星表面高度
解得:
探测器悬停时具有的重力势能
26.-37500J,37500J,37500J
【解析】
【分析】
【详解】
重力对他做功为
W=-mgh=-50×10×150×sin30°=-37500J
他克服重力做功为
W=mgh=50×10×150 ×sin30°=37500J
由
W G=-△E P
可知重力势能增加37500J。
27.(1)5000N/m ;(2)5m;(3)1.1m;2525J
【解析】
【分析】
【详解】
(1)床面下沉x0=0.1m时,运动员受力平衡,有
mg=kx0
解得
k=5×103N/m.
F-x图线如图所示.
(2)运动员从x=0处离开床面,开始腾空,由运动的对称性知其上升、下落的时间相等,
解得
hm=5.0m
(3)参照由速度时间图线求位移的方法可知F-x图线下的面积等于弹力做的功,从x处到x=0处,弹力做的功
运动员从x1处上升到最大高度hm的过程,根据动能定理可得
解得
x1=1.1m
对整个预备运动过程分析,由题设条件以及功和能的关系,有
解得
W=2525J.
28.(1)5N;(2)9J;(3)6m/s
【解析】
【详解】
(1)小球受到重力的大小
(2)取B点的重力势能为零,则小球在A点重力势能
(3)小球由A摆至B过程,由动能定理可得
解得小球到B点速度
29.(1)54J;(2)18W
【解析】
【详解】
(1)根据牛顿第二定律可求出加速度
则物体在3s末的速度
物体在3s内的位移
力F做的功
(2)力F在3s内的平均功率
30.(1)4180J (2)增加了4180J
【解析】
【详解】
(1)运动员跳过6.14m,其重心至少升高6.14m高度处.该运动员升高1.83m,重心的高度约为0.915m,故跳过6.14m的高度,至少克服重力做功:
;
(2)运动员跳到6.14m高度处过程中,其重力做负功,所以运动员的重力势能增加,克服重力做的功就等于重力势能的增加量,所以重力势能增加了4180J.
31.n(n-1)mgh
【解析】
【分析】
【详解】
取n块砖的整体为研究对象,平放时重心的高度
h1=
选取地面为参考平面,其相应的重力势能为
Ep1=
n块砖被竖直叠放后的重心高度
h2=
其相应的重力势能为
Ep2=nmg·=
故
ΔEp=Ep2-Ep1=-=n(n-1)mgh
答案第1页,共2页
答案第1页,共2页
