第八章 动能和动能定理基础巩固拓展练习(word版含答案)
文档属性
| 名称 | 第八章 动能和动能定理基础巩固拓展练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 969.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-15 07:18:54 | ||
图片预览



文档简介
2019人教版必修第二册 第八章 3 动能和动能定理 基础巩固 拓展练习
一、单选题
1.木块在水平恒力F作用下,由静止开始在水平路面上前进S,随即撤去此恒力后又前进2S才停下来,设运动全过程中路面情况相同,则木块在运动中所获得的动能的最大值为( )
A. B. C.FS D.
2.李佳同学在学校秋季田径运动会上参加了高一组径赛项目的决赛,在终点冲刺时他的动能最接近( )
A. B. C. D.
3.如图,半圆形光滑轨道固定在水平地面上,半圆的直径与地面垂直,一小物块以速度v从轨道下端滑入轨道,并恰能从轨道上端水平飞出,则轨道半径为(重力加速度为g)( )
A. B. C. D.
4.如图所示,光滑轨道MO和ON底端对接,且,M、N两点高度相同.小球自M点由静止滚下,忽略小球经过O点时的能量损失,以v、x、a、分别表示小球的速度、位移、加速度和动能四个量的大小.下列图象中能正确反映小球自M点到N点运动过程的是
A. B. C. D.
5.如图所示,固定在竖直平面内的光滑圆管轨道ABCD,其A点与圆心等高,D点为最高点,今使质量为m的小球自A点正上方h高处由静止释放,且从A处进入圆管轨道并经过D点刚好落回A点,则下列说法中正确的是
A.只要小球就会落回到A点
B.当时小球一定过最高点D并落回到A点
C.当小球刚好落回到A点时,小球在D点所受的弹力大小为,方向向下
D.当小球刚好落回到A点时,小球在D点所受的弹力大小为,方向向上
6.下列物理量属于矢量的是( )
A.动能 B.功率 C.向心加速度 D.周期
7.战斗机以一定的水平初速度着陆甲板时,若飞机勾住阻拦索减速,飞机在甲板上滑行的距离将大大减小.着舰使用阻拦索时,下列说法正确的是( )
A.战斗机的动能变化量变大
B.战斗机的惯性减少得快
C.战斗机的加速度变大
D.战斗机的速度减少得多
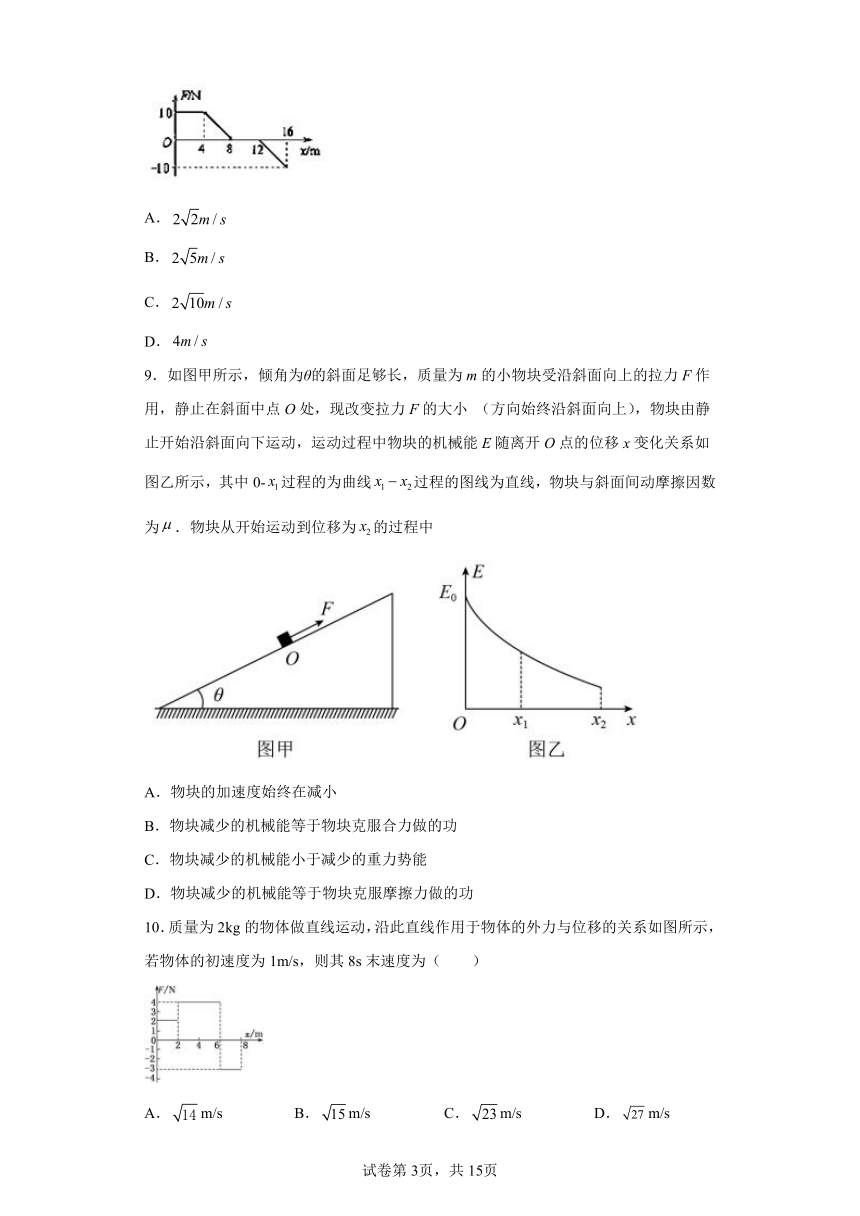
8.物体在变力作用下沿水平方向做直线运动,物体质量,F随坐标的变化情况如图所示.若物体在坐标原点处由静止出发,不计一切摩擦.借鉴教科书中学习直线运动时由图象求位移的方法,结合其他所学知识,根据图示的图象,可求出物体运动到处时,速度大小为( )
A.
B.
C.
D.
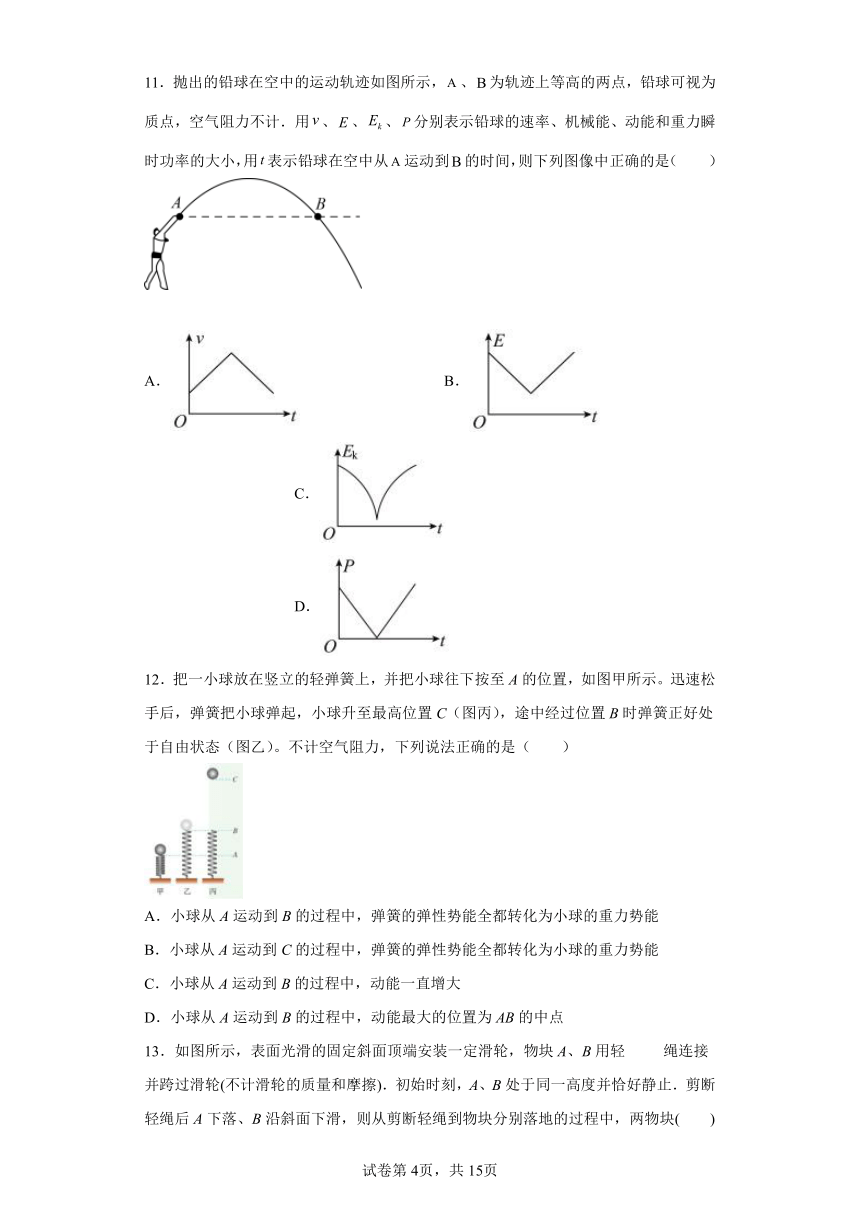
9.如图甲所示,倾角为θ的斜面足够长,质量为m的小物块受沿斜面向上的拉力F作用,静止在斜面中点O处,现改变拉力F的大小 (方向始终沿斜面向上),物块由静止开始沿斜面向下运动,运动过程中物块的机械能E随离开O点的位移x变化关系如图乙所示,其中0-过程的为曲线过程的图线为直线,物块与斜面间动摩擦因数为.物块从开始运动到位移为的过程中
A.物块的加速度始终在减小
B.物块减少的机械能等于物块克服合力做的功
C.物块减少的机械能小于减少的重力势能
D.物块减少的机械能等于物块克服摩擦力做的功
10.质量为2kg的物体做直线运动,沿此直线作用于物体的外力与位移的关系如图所示,若物体的初速度为1m/s,则其8s末速度为( )
A.m/s B.m/s C.m/s D.m/s
11.抛出的铅球在空中的运动轨迹如图所示,、为轨迹上等高的两点,铅球可视为质点,空气阻力不计.用、、、分别表示铅球的速率、机械能、动能和重力瞬时功率的大小,用表示铅球在空中从运动到的时间,则下列图像中正确的是( )
A. B. C. D.
12.把一小球放在竖立的轻弹簧上,并把小球往下按至A的位置,如图甲所示。迅速松手后,弹簧把小球弹起,小球升至最高位置C(图丙),途中经过位置B时弹簧正好处于自由状态(图乙)。不计空气阻力,下列说法正确的是( )
A.小球从A运动到B的过程中,弹簧的弹性势能全都转化为小球的重力势能
B.小球从A运动到C的过程中,弹簧的弹性势能全都转化为小球的重力势能
C.小球从A运动到B的过程中,动能一直增大
D.小球从A运动到B的过程中,动能最大的位置为AB的中点
13.如图所示,表面光滑的固定斜面顶端安装一定滑轮,物块A、B用轻 绳连接并跨过滑轮(不计滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好静止.剪断轻绳后A下落、B沿斜面下滑,则从剪断轻绳到物块分别落地的过程中,两物块( )
A.落地时速度相同
B.运动时间相同
C.重力势能的变化量相同
D.重力的平均功率相同
14.一质点从t=0时刻开始做自由落体运动,E表示下落过程中的动能,x表示下落的位移,t表示下落的时间。下列图像中可能正确的是( )
A. B.
C. D.
15.如图为一发光轨道yoyo球结构,yoyo球具有磁性,可以紧贴铁质的轨道外侧做圆周运动,若不考虑球与轨道之间的摩擦,且yoyo球与轨道之间的磁力大小不变。则停止甩动yoyo球让其转动起来后( )
A.做的是匀速圆周运动
B.在最高点速度不能小于
C.在最高点对轨道的压力大于最低点对轨道的压力
D.由于有磁力作用,yoyo球运动过程中机械能不守恒
16.在“探究功与速度变化的关系”的实验中,可以得到橡皮筋对小车做的功W与小车获得的速度大小v之间的关系,下列关系正确的是( )
A.W∝v B.W∝v2 C. D.
17.如图所示,一弹簧下端系一物体,用手托着物体,使弹簧保持原长l0.现使物体缓缓地下降到平衡位置O,并保持静止。在此过程中,重力对物体做功的大小为Wg,弹簧的弹力对物体做功的大小We,手的支持力对物体做功的大小为W。则有( )
A.W=Wg B.WW
18.如图,站在向右作匀加速直线运动的车厢内的人向前推车壁,下列说法正确的是
A.人对车的作用力仅是手的推力
B.车对人的摩擦力大于车对人的推力
C.因为人相对车没有动,所以合外力为零
D.该人对车做正功
19.如图,水从竖直放置的花洒喷出,落在水平地面上。某时刻从各喷口处水平喷出初速度相等的一小段水柱,在空中的运动都可视为平抛运动,则( )
A.各段水柱同时落地
B.各段水柱落地时的速度大小相等
C.从最低点喷出的水柱落地时的水平射程最大
D.从最高点喷出的水柱落地时的速度偏向角最大
二、多选题
20.如图所示,花样滑冰双人自由滑比赛时的情形,男运动员以自己为转动轴拉着女运动员做匀速圆周运动,若男运动员转速为30r/min,手臂与竖直方向夹角约为60°,女运动员质量是50kg,她触地冰鞋的线速度为4.7m/s,则下列说法正确的是( )
A.女运动员做圆周运动的加速度为
B.女运动员触地冰鞋做圆周运动的半径约为2m
C.男运动员手臂拉力约是850N
D.男运动员手臂拉力约是500N
21.排球课上小明同学练习垫球,现将质量为m的排球,以竖直向上垫起,由于空气阻力作用,排球上升时加速度大小为g,小明在原垫起点接住排球,排球在整个运动过程中受到的阻力大小恒定。关于排球的运动,下列说法正确的是( )
A.整个过程阻力不做功
B.整个过程克服阻力做
C.返回垫起点时重力的瞬时功率为
D.返回垫起点时重力的瞬时功率为
22.铅块质量为0.8kg,以初速度从下端滑上很长的斜面,斜面倾角为37°,铅块到达中途某点损失机械能,损失动能,只考虑斜面阻力,,,,则有( )
A.铅块以向上滑
B.铅块不可返回下端处,全程损失机械能
C.铅块与斜面摩擦系数为0.5
D.铅块可返回下端处,到下端剩余动能
23.如图所示,当小车向右加速运动时,物块M相对车厢静止于竖直车厢壁上,当车的加速度增大时( )
A.M对车厢壁的压力不变 B.M受静摩擦力增大
C.M受静摩擦力不变 D.M仍相对于车厢静止
24.关于下列实验的说法正确的是( )
A.在“探究加速度与力、质量的关系”实验中,需要平衡摩擦力
B.在“探究求合力的方法”实验中,两个分力与合力的标度一定要相同
C.在用橡皮筋做“探究功与速度变化的关系”实验时,可以求得做功的具体数值
D.在“验证机械能守恒定律”的实验中,可以用重力加速度计算重锤在某时刻的速度
三、实验题
25.某实验小组采用如图甲所示的实验装置来探究功与速度变化的关系。
(1)下列关于该实验的说法正确的是_______;
A.将木板一端垫高,使小车的重力沿斜面向下的分力与摩擦阻力平衡。方法是轻推小车,根据打点计时器打在纸带上的点是否均匀判断小车是否做匀速运动
B.测小车速度时,应选纸带上的点迹距离均匀增加的部分,也就是选小车做匀加速运动的部分
C.橡皮筋应选规格一样的。力对小车做的功以一条橡皮筋做的功为单位即可,不必计算出具体数值,而只是看第2次、第3次……实验中的是第1次的多少倍,简化数据的测量和处理
D.小车质量应小一些,使纸带上打的点少一些
(2)在正确操作的情况下,该小组某次所打的纸带如图乙所示。为了测量橡皮筋做功后小车获得的速度,应选用纸带上的_______(填“”“”或“”)段进行测量;若使用的交流电的频率为,则小车最终获得的速度是______(保留3位有效数字)。
(3)以为纵坐标,为横坐标,利用实验数据作出如图所示的图象,该图象为一条直线,说明_______。根据功与能的关系,动能的表达式中可能包含这个因子,分析实验结果的单位关系,与图线斜率有关的物理量应是_______。
(4)假设没有完全消除摩擦力和其他阻力,认为每次这些力都一样,则从理论上分析,下列图中正确反映关系的是_______。
A. B. C. D.
26.某实验小组要探究力对物体做功与物体获得速度的关系,选取的实验装置如图所示,实验主要步骤如下:
(1)实验时,为使小车只在橡皮筋作用下运动,在未连接橡皮筋时将木板的左端用小木块垫起,使木板倾斜合适的角度,打开打点计时器,轻推小车,得到的纸带应该是____填(“甲”或“乙”)
(2)使小车在一条橡皮筋的作用下由静止弹出,沿木板滑行,这时橡皮筋对小车做的功为W;
(3)再用完全相同的2条、3条……橡皮筋作用于小车,每次由静止释放小车时橡皮筋的______________(填写相应实验条件),使橡皮筋对小车做的功分别为2W、3W…
(4)分析打点计时器打出的纸带,分别求出小车每次获得的最大速度v1、v2、v3…
(5)作出W-v图像,则下列图像符合实际的是_______
27.用如图所示的装置做“探究动能定理”的实验时,下列说法正确的是__________.
A.为了平衡摩擦力,实验中可以将长木板的左端适当垫高,使小车在不挂橡皮筋时能拉着穿过打点计时器的纸带保持匀速运动
B.每次实验中橡皮筋的规格要相同,拉伸的长度要一样
C.可以通过改变小车的质量来改变拉力做功的数值
D.可以通过改变橡皮筋的条数改变拉力做功的数值
E.通过打点计时器打下的纸带来测定小车加速过程中获得的最大速度
F.实验中要先释放小车再接通打点计时器的电源
G.通过打点计时器打下的纸带来测定小车加速过程中获得的平均速度
四、解答题
28.从离地面h=80m高处水平抛出的物体,着地时的水平位移为x=20m,求:
(1)运动时间;
(2)初速度大小;
(3)落地时速度大小及它与水平方向夹角的正切;
(4)在空中运动的第2s内速度的变化△v.
29.追寻守恒量是物理学的重要研究内容,在高中阶段我们探索守恒量时,除了实验手段,也常借助已有理论来进行分析。已知重力加速度为g。供暖系统、自来水系统都是通过管道运送液体的。管内液体稳定流动时具有这样的特点:①管内各处液体体积无法压缩且密度均相同;②管内各处液体流速不随时间改变。如图所示,选取横截面C和横截面D之间的液体为研究对象,当C处液体流动很小一段距离,到达时,D处液体正好流动到处。已知液体密度为,C处的压强为、流速为、高度为,D处的压强为、流速为、高度为,C处管道半径为R,C与间距离为d,且R、d均远远小于。不计管道对液体的阻力,不考虑液体的黏滞性。在C、D间的液体流动至、的过程中
(1)求横截面C左侧液体对研究对象所做的功;
(2)求重力对研究对象所做的功;
(3)研究表明,可运用动能定理对C、D间的液体进行分析。请依据动能定理探索压强p、流速u、高度h是否也存在着某种守恒的关系。若存在,请写出关系式;若不存在,请说明理由。
30.如图所示,水平桌面上的轻质弹簧左端固定,右端与静止在O点质量为m=1kg的小物块接触而不连接,此时弹簧无形变.现对小物块施加F =" 10" N水平向左的恒力,使其由静止开始向左运动.小物块在向左运动到A点前某处速度最大时,弹簧的弹力为 6 N,运动到A点时撤去推力F,小物块最终运动到B点静止.图中OA =" 0.8" m,OB =" 0.2" m,重力加速度g =" 10" m/s2.求小物块:
(1)与桌面间的动摩擦因数μ;
(2)向右运动过程中经过O点的速度;
(3)向左运动的过程中弹簧的最大压缩量.
31.某游乐场的滑梯可以简化为如图所示竖直面内的ABCD轨道,AB为长L=5m、倾角的斜轨,BC为水平轨道,CD为半径R=14m的圆弧轨道。轨道AB段粗糙,其余各段均光滑,一小孩(可视为质点)从A点以初速度v0=3m/s下滑,沿轨道运动到C点时的速度vC=7m/s,全程不滑离轨道(不计经过B点时的能量损失)。已知该小孩的质量m=20kg,取sin37°=0.6,cos37°=0.8,不计空气阻力,设最大静摩擦力等于滑动摩擦力。求:
(1)小孩沿轨道AB运动过程中重力所做的功;
(2)该小孩第一次经过圆弧C点时,对圆弧轨道的压力FN;
(3)该小孩与AB轨道间的动摩擦因数;
(4)该小孩在轨道AB上运动的总路程s。
32.某同学用锤子将一个小铁钉钉进墙壁中.钉子进入墙壁过程中,所受阻力f与钉进深度x间的关系如图所示.铁钉重力可以忽略不计,则:
(1) 该同学第一次敲击铁钉,发现铁钉进入深度为,求该过程锤子对铁钉做的功W0;
(2) 若每一次敲击,锤子对铁钉做功恒为W0,则敲击两次,铁钉进入的深度为多少;
(3) 在(2)的条件下,若要使铁钉进入深度为4x0,应敲击铁钉几次.
33.在光滑的水平面上放着物体A和小车B,如图所示,小车长L=2m,M=4kg,A的质量m=1kg,μAB=0.2,假设最大静摩擦力等于滑动摩擦力,求:(g取10m/s2)
(1)若加在小车上的力F=5N,在这种情况下,在2s时间内F对车做功是多少?摩擦力对A做功多少?小车动能增加多少?
(2)若加在小车上的力F=12N,在这种情况下,在2s时间内F对车做功是多少?摩擦力对A做功多少?小车动能增加多少?
34.如图所示,在倾角θ=30°的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量均为m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现开始用一沿斜面方向的力F拉物块A使之向上匀加速运动,当物块B刚要离开C时F的大小恰为2mg.问:
(1)从F开始作用到物块B刚要离开C的过程中弹簧弹力对物块A做的功;
(2)物块B刚要离开C时物块A的动能;
(3)从F开始作用到物块B刚要离开C的过程中力F做的功.
35.第24届冬奥会将于2022年由北京和张家口两个城市联合举办,跳台滑雪是其中最具观赏性的项目之一,其空中翻转动作优美,深受观众喜爱。某滑道示意图如图所示,长直助滑道AB与光滑圆弧形滑道BC相切于B点,且AB与B、C两点所在水平面的夹角,助滑道AB长L=90m。圆弧滑道BC与水平安全平台CD连接,CD长x=38.4m。平台CD与曲线着陆坡DE连接,D、E两点高度差为35m。着陆坡DE下端衔接一段圆心角的圆弧轨道,圆弧轨道最低点与水平终点区FG相切。质量m=80kg(含滑板等装备)的运动员(可视为质点)从A处由静止开始自由下滑(运动员不做功),经C点飞起,恰好从D点进入曲线着陆坡DE。重力加速度,运动员在空中运动过程中可视为质点,忽略运动过程中空气的作用。
(1)滑板克服滑道AB阻力做功为多少;
(2)某次试赛中,该运动员从A处由静止开始加速下滑(运动员做功),恰从E点沿切线进入圆弧轨道,实现完美一跃。求此过程中运动员做的功。
36.如图甲所示,在公元1267-~1273年闻名于世的“襄阳炮”其实是一种大型抛石机。将石块放在长臂一端的石篮中,在短臂端挂上重物。发射前将长臂端往下拉至地面,然后突然松开,石袋中的石块过最高点时就被拋出。现将其简化为图乙所示。将一质量m=80kg的可视为质点的石块装在长m的长臂末端的石篮中,初始时长臂与水平面成30°,松开后,长臂转至竖直位置时石块被水平抛出落在水平地面上。石块落地点与O点的水平距离s=100m。忽略长臂、短臂和石袋的质量,不计空气阻力和所有摩擦,g=10m/s2,求:
(1)石块水平抛出时的初速度v0;
(2)石块从A到最高点的过程中石篮对石块做功W;
(3)石块圆周运动至最高点时,石块对石篮的作用力F。
37.如图所示,一弧形轨道与足够长的水平轨道平滑连接,水平轨道上静止一小球B。从弧形轨道上距离水平轨道高h处由静止释放一质量为m的小球A,A球沿轨道下滑后与B球发生弹性正碰,碰后A球被弹回,A球重新下滑到水平轨道后,与B球间的距离保持不变。所有接触面均光滑。求:
(1)碰撞前瞬间A球的速度大小;
(2)B球的质量和碰撞结束时A球的速度大小;
(3)碰撞结束时A对B的冲量。
38.滑板运动是青少年喜爱的一项活动。如图甲所示,滑板运动员以某一初速度从A点水平离开h=0.8m高的平台,运动员(连同滑板)恰好能无碰撞的从B点沿圆弧切线进入竖直光滑圆弧轨道,然后由C点滑上涂有特殊材料的水平面,水平面与滑板间的动摩擦因数从C点起按图乙规律变化,已知圆弧与水平面相切于C点,B、C为圆弧的两端点。圆弧轨道的半径R=1m;O为圆心,圆弧对应的圆心角=53°,已知,,,不计空气阻力,运动员(连同滑板)质量m=50kg,可视为质点,试求:
(1)运动员(连同滑板)离开平台时的初速度v0;
(2)运动员(连同滑板)通过圆弧轨道最低点对轨道的压力;
(3)运动员(连同滑板)在水平面上滑行的最大距离。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【详解】
对全程由动能定理得:Fs-f 3s=0,则:f=F,由题意可知,当拉力撤销的时候,木块获得最大动能:由动能定理可知:Ekm=Fs-fs=Fs-Fs=Fs;故选D.
2.B
【解析】
【分析】
【详解】
假设李佳同学质量为60kg,重点冲刺速度为10m/s,则动能为
故选B。
3.B
【解析】
【详解】
设半圆的半径为R,从轨道下端滑入到上端过程中,根据动能定理得
在最高点,根据牛顿第二定律有
mg=
解得轨道半径R=.
A.轨道半径为,与分析不一致,故A错误;
B.轨道半径为,与分析相一致,故B正确;
C.轨道半径为,与分析不一致,故C错误;
D.轨道半径为,与分析不一致,故D错误.
4.B
【解析】
【详解】
因为在MO和NO段的平均速度相等,位移之比为1:2,则时间之比为1:2;对于速度时间图线,小球运动过程中,在两个斜面上都沿斜面做匀变速运动;对于位移时间图线,由于在两个斜面上都是匀变速运动,根据位移时间关系公式,可知位移时间图象是曲线,该图线错误,故A错误;做匀变速直线运动,速度先增加后减小,根据速度时间关系公式,可知两段运动过程中的图都是直线,且MO段图线的斜率绝对值大于ON段图线斜率的绝对值,该图线正确,故B正确;对于加速度时间图线,加速度的大小与斜面的倾角大小有关,倾角确定,加速度大小确定,该图线错误,故C错误;对于动能时间图线,速度与时间是一次函数关系,动能与速度的二次方成正比,故动能与时间也是二次函数关系,该图线错误,故D错误.故选B.
点睛:研究两个物理量之间的关系图线,关键是根据物理规律得出两个量的表达式,从而分析判断,这是解决图象题的常用方法.
5.D
【解析】
【分析】
【详解】
A.小球自A点正上方h高处由静止释放到A点,有机械能守恒得
从A点到D点,机械能守恒
从D点到A点,小球做平抛运动
以上几个式子联立,解得
所以当时小球一定过最高点D并落回到A点,AB错误;
CD.在D点,受力分析有
解得
且方向向上,C错误,D正确。
故选D。
6.C
【解析】
【详解】
矢量既有大小又有方向,标量只有大小没有方向;
ABD.动能、功率、周期,都只有大小,没有方向,为标量,ABD错误;
C.向心加速度既有大小又有方向,为矢量,C正确。
故选C。
7.C
【解析】
【详解】
AD. 两种情况下,战斗机的初末动能相同,动能的变化量相同,速度减小的一样多,故A项错误,D错误;
B. 惯性只与物体的质量有关,惯性不变,故B项错误;
C. 根据速度位移公式可知,舰使用阻拦索时滑行距离减小,战斗机的加速度变大,故C项正确;
8.B
【解析】
【详解】
根据图象求位移的方法可知图象的面积代表力做的功,所以全程动能定理得:,且联立解得:,ACD错误B正确.
9.C
【解析】
【分析】
【详解】
A.由图可知,物块向下运动的过程中,其中O~x1过程的图线为曲线,斜率逐渐减小,而斜率
联立可知
斜率减小,则减小,物块受到的合外力
不一定减小,由牛顿第二定律可知,物块的加速度不一定减小;在x1~x2过程的图线为直线,k不变,则物块的加速度不变,A错误;
BD.物块向下运动的过程中,重力、拉力与摩擦力做功,物块减少的机械能等于拉力与摩擦力做功,不等于物块克服合力做的功,BD错误;
C.物块由静止开始沿斜面向下运动,由动能定理可知
重力势能减小量等于重力功WG,机械能的减小量等于 ,所以物块减少的机械能小于减少的重力势能,C正确。
故选C。
10.B
【解析】
【详解】
外力与位移图象与坐标轴围成的面积表示外力所做的功,由图可知
根据动能定理得
解得
故选B。
11.D
【解析】
【详解】
AB.铅球做斜上抛运动,机械能守恒,重力势能先增加后减小,故动能先减小后增加,速度先减小后增加,故AB错误;
C.以初始位置为零势能面,抛出时速度方向速度为,铅球的机械能守恒,则
故图象为抛物线,故C错误;
D.速度的水平分量不变,竖直分量先减小到零,后反向增加,故根据
重力的功率先均匀减小后均匀增加,故D正确;
故选D。
12.B
【解析】
【详解】
A.小球从A运动到B的过程中,因小球在B点具有速度,所以弹簧的弹性势能一部分转化为小球的重力势能,还有一部分转化为小球的动能,故A错误;
B.小球从A运动到C的过程中,由于小球在C点的速度为零,则弹簧的弹性势能全都转化为小球的重力势能,故B正确;
C.小球从A运动到B的过程中,先向上作加速运动,后作减速运动,所以其动能不是一直增大,而是先增大后减小,故C错误;
D.小球从A运动到B的过程中,动能最大的位置为小球的重力等于弹簧的弹力时的位置,而不一定是AB的中点位置,故D错误。
故选B。
13.D
【解析】
【详解】
剪断轻绳后A自由下落,B沿斜面下滑,AB都只有重力做功,根据机械能守恒定律得,得,可知两个物体落地速度大小相等,但方向不同,所以落地速度不同,A错误;根据牛顿第二定律可知B的加速度为,即加速度不同.对A,由,得;对B,由,则得,可知运动时间不同,重力的平均功率为,,由于,故,B错误D正确;未间断细绳前,,故两者的质量不同,下落高度相等,故重力势能变化量不同,C错误.
14.C
【解析】
【分析】
【详解】
AB.根据自由落体运动运动规律有
则动能
由数学知识知,图像应为开口向上的抛物线,故AB错误;
CD.根据动能定理,有
由数学知识知,图像为一条过原点的倾斜直线,故C正确,D错误。
故选C。
15.C
【解析】
【分析】
【详解】
A.停止甩动yoyo球让其转动起来后重力对球做功,则yoyo球做变速圆周运动,故A错误;
B.yoyo球在最高点时重力与磁力的合力和弹力等大反向时,球的速度为0,即在最高点最小速度为0,故B错误;
C.在最高点由牛顿第二定律有
在最低点由牛顿第二定律有
从最高点到最低点由动能定理可知
得
则在最高点对轨道的压力大于最低点对轨道的压力,故C正确;
D.由于磁力方向始终与速度方向垂直,则磁力不做功,球在运动过程中只有重力做功,则机械能守恒,故D错误。
故选C。
16.B
【解析】
【详解】
小车在橡皮筋拉力作用下由静止开始运动,初动能为零,由动能定理可知
物体的质量一定,则
故选B。
17.B
【解析】
【详解】
用手托着物体,使物体缓缓地下降到平衡位置O,在此过程中物体状态不变,动能变化量为0,根据动能定理得
变形得
故选B。
18.B
【解析】
【详解】
对人分析可知,人受重力、车向左的弹力以及地面向右的摩擦力;故人对车有向左的摩擦力和推力;故A错误;对人分析由牛顿第二定律可知,人受到的合力向右,故摩擦力大于车对人的推力;故B正确;C错误;由于车对人的合力向右,则可知人对车的合力一定向左,则由功的公式可知,人对车做负功;故D错误;故选B.
【点睛】
此题涉及到牛顿第二定律的应用和力的作用的相互性,解决此类题目要结合作用力和反作用力考虑,同时注意功的分析和判断方法.
19.D
【解析】
【详解】
A.根据平抛运动公式
解得
由于各段水柱的高度不一样,所以不能同时落地,故A错误;
B.落地时竖直方向的分速度为
水平方向的分速度为
所以落地速度大小为
由于高度不相等,所以各段水柱落地时的速度大小也不相等。故B错误;
C.水平位移为
故高度最大的水柱水平位移最大。故C错误;
D.设水柱落地时的速度偏向角为,则
根据公式可知,高度越大的水柱,下落的时间越长,就越大,故D正确。
故选D。
20.AC
【解析】
【详解】
A.女运动员做圆周运动的角速度等于男运动员转动的角速度,则
rad/s
A正确;
B.根据:
得:m,B错误;
CD.拉力沿水平方向上的分力提供向心力,则有:
解得,C正确,D错误。
故选AC。
【点睛】
关键是知道两运动员运动的角速度相同,然后根据转速的大小得出圆周运动的角速度,根据拉力沿水平方向上的分力提供向心力。
21.BD
【解析】
【分析】
【详解】
AB.排球上升过程,根据牛顿第二定律,有
带入数据,可得
该过程排球的位移大小为
则整个运动过程中,阻力做功为
带入数据,可得
所以整个过程克服阻力做功为
故A错误;B正确;
CD.设返回垫起点时排球速度为,整个过程中由动能定理,有
整理,可得
所以返回垫起点时重力的瞬时功率为
故C错误;D正确。
故选BD。
22.AD
【解析】
【详解】
BC.向上减速运动重力势能增加,动能减小,损失的机械能为摩擦生热,根据能量守恒可得
联立可解得
上升到某点的位移为,则有
解得
由于,则铅块可返回下端。BC错误;
A.铅块受沿斜面向下的摩擦力和沿斜面向下重力的分力,由牛顿第二定律得
解得
A正确;
D.上升到最高点时的位移为
返回下端时,根据动能定理可得
解得
D正确。
故选AD。
23.CD
【解析】
【详解】
对物块M,水平方向
FN=ma
竖直方向
f=mg
则当车的加速度增大时M对车厢壁的压力增大,最大静摩擦力变大,则M仍相对于车厢静止,M受静摩擦力不变。
故选CD。
24.AB
【解析】
【详解】
A、在“探究加速度与质量、外力之间的关系”实验中,需要平衡摩擦力,故A正确;
B、在“探究求合力的方法”实验中,两个分力与合力的标度一定要相同,故B正确;
C、实验时,每次保持橡皮筋的形变量一定,当有n根相同橡皮筋并系在小车上时,n根相同橡皮筋对小车做的功就等于系一根橡皮筋时对小车做的功的n倍,这个设计很巧妙地解决了直接去测量力和计算功的困难,故实验中不需要测出一条橡皮筋对小车做功W的数值,故C错误;
D、在验证机械能守恒的实验中,由于存在阻力物体实际下落的加速度小于重力加速度,不可以用重力加速度计算重锤在某时刻的速度,应该运用某段时间内的平均速度等于中间时刻的瞬时速度,故D错误;
故选AB.
25. AC##CA BC 0.686 合外力对小车做的功,与小车的速度的平方成正比 小车的质量 B
【解析】
【详解】
(1)[1]A.小车与木板间有摩擦,将木板一端垫高,平衡摩擦力,轻推小车打点计时器在纸带上的点迹均匀小车做匀速运动,故A正确;
B.测小车速度时,应选纸带上的点迹均匀的部分进行计算,故B错误;
C.因为此实验改变做功是通过改变橡皮筋条数来实现的,则只要保证小车质量不变即可,不必测小车质量,也不必测功的具体值,只是用W、2W、3W等表示,简化数据的测量和处理。故C正确;
D.小车质量不能太大或太小,保证纸带上的点迹不要过于密集或稀疏,方便处理数据,故D错误。
故选AC。
(2)[2]测小车速度时,应选纸带上的点迹均匀的部分进行计算,故应选BC段;
[3]小车最终获得的速度是
(3)[4]合外力对小车做的功,与小车的速度的平方成正比;
[5]由图可得v随W变化的表达式为v2=kW,由等式两端的物理量单位可知,左侧单位为,右侧单位为J,所以k的单位为
所以与图线斜率有关的物理量应是小车的质量。
(4)[6]若没有完全消除摩擦力和其他阻力,橡皮筋对小车的功有部分用于克服阻力做功,没有全部转化为小车的动能,故B正确。
故选B。
26. 乙 伸长量(或形变量、长度等)都相同 D
【解析】
【详解】
(1)[1]平衡摩擦力后,小车应做匀速运动,所以纸带应该是图乙;
(2)[2]橡皮条拉力是变力,采用倍增法增加功;即使小车在一条橡皮筋的作用下由静止弹出,这时橡皮筋对小车做的功为W;再用完全相同的2条、3条…橡皮筋作用于小车,每次由静止释放小车时橡皮筋的伸长量都相同,使橡皮筋对小车做的功分别为2W、3 W…
(5)[3]功与速度的平方相对应,所以图象应为D。
27.ABDE
【解析】
【详解】
A、小车在水平面运动时,由于受到摩擦阻力导致小车速度在变化,所以适当倾斜以平衡摩擦力,小车所能获得动能完全来于橡皮筋做的功,所以实验中可以将长木板的左端适当垫高,使小车在不挂橡皮筋时能拉着穿过打点计时器的纸带保持匀速运动,故A正确;
B、实验中每根橡皮筋做功均是一样的,所以所用橡皮筋必须相同,且伸长的长度也相同,故B正确;
C、是通过改变橡皮筋的条数来改变拉力做功的数值,故C错误;
D、每次实验时橡皮筋伸长的长度都要一致,则一根做功记为W,两根则为2W,可以通过改变橡皮筋的条数改变拉力做功的数值,故D正确;
F、只要使用打点计时器的实验,都是先接通电源后释放纸带,故F错误;
EG、由于小车在橡皮筋的作用下而运动,橡皮筋对小车做的功与使小车能获得的最大速度有关,故E正确, G错误;
故选ABDE.
28.(1)4s (2)5m/s(3)20.6m/s; 8(4)10m/s
【解析】
【详解】
试题分析:(1)运动时间
(2)初速度大小
(3)落地时竖直速度大小:vy=gt=40m/s
落地的速度:
落地的速度与水平方向夹角的正切;
(4)在空中运动的第2s内速度的变化△v=gt=10×2=20m/s.
考点:平抛运动
【名师点睛】本题就是对平抛运动规律的直接考查,掌握住平抛运动的规律就能轻松解决;要知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.
29.(1);(2);(3)
【解析】
【详解】
(1)横截面C左侧液体对研究对象所做的功
(2)C、D间液体流动至、间,可等效为、D间液体位置不变,C、间液体流动至D、间。C、间液体质量
重力对研究对象所做的功
(3)在相同的时间内,流过C处截面水的体积与流过D处截面水的体积相同。由C,间液体体积
可知
设D处管道面积为,D、间距离为x,则D、间液体体积
横截面D右侧液体对研究对象所做的功
由动能定理,合外力做功
即
整理得
所以压强、流速、高度是满足守恒的关系,即
为守恒量。
30.(1)0.4(2)(3)0.9m
【解析】
【详解】
试题分析:(1)小物块速度达到最大时,加速度为零.
(2)设向右运动通过O点时的速度为v0,由动能定理列出:
解得
(3)设撤去F推力后,小物块继续向左运动x的距离,弹簧的压缩量最大值为.取小物块运动的全过程,根据动能定理列出:
则
考点:动能定理;牛顿定律.
31.(1)600J;(2)270N,方向向下;(3)0.25;(4)17.25m
【解析】
【分析】
【详解】
(1)小孩沿轨道AB运动过程中重力所做的功为
(2)小孩第一次经过圆弧C点时,根据牛顿第二定律有
代入数据求得
FN=270N
根据牛顿第三定律,小孩对轨道的压力为270N,方向向下
(3)小孩从A点下滑,沿轨道运动到C点,根据动能定理有
代入数据求得
(4)由于
小孩从A点下滑,沿轨道运动最终将停止在水平BC段,根据动能定理有
代入数据求得
s=17.25m
32.(1) (2) (3)28次
【解析】
【详解】
(1) 该同学第一次敲击铁钉,发现铁钉进入深度为,如图知
该过程锤子对铁钉做的功
(2) 敲击两次,铁钉进入的深度为x,根据题意知x小于x0,此时
则有:
解得
(3) 当铁钉进入深度为x0时,摩擦力等于f0,此时需要做功为:
铁钉从x0到4x0过程中,需要做功为:
故要使铁钉进入深度为4x0,应敲击铁钉24+4=28次
33.(1)10J,2J,8J(2)60J,8J,50J
【解析】
【详解】
设A和B以共同加速度运动时F的最大值为F0,根据牛顿第二定律,对A、B整体有
对A单独有
解得
(1)当F=5N2s时间内整体的位移大小为
AB间的摩擦力大小为
f=ma=1N
F对车做功
WF=Fx=10J
摩擦力对A做功
Wf=fx=2J
根据动能定理可知,合外力对车做功等于其动能增量,即
ΔEk=(F-f)x=8J
(2)当F=12N>F0时,A、B将出现相对滑动,此时A的加速度大小为
aA=a0=2m/s2
B的加速度大小为
在2s时间内A的位移大小为
B的位移大小为
AB间的摩擦力大小为
F对车做功
WF′=FxB=60J
摩擦力对A做功
Wf′=f′xA=8J
同(1)理可知小车动能增量为
ΔEk′=(F-f′)xB=50J
34.(1)0(2)(3)
【解析】
【详解】
(1)(2)令x1表示未加F时弹簧的压缩量,由胡克定律和牛顿定律可知:
mgsin30°=kx1
令x2表示B 刚要离开C时弹簧的伸长量,a表示此时A 的加速度,由胡克定律和牛顿定律可知:
kx2=mgsin30°
F-mgsin30°-kx2=ma
将F=2mg和θ=30°代入以上各式,解得:a=g
由x1+x2=at2
解得:
物块B刚要离开C时,物块A的速度为:v=at=g
故动能为:
此时弹簧的伸长量和F开始作用时的压缩量相同,弹簧的弹性势能改变量为零,故弹簧弹力做功为零;
(3)由动能定理得:
WF-mg(x1+x2)sin30°=mv2
解得:
35.(1)27200J;(2)20000J
【解析】
【分析】
【详解】
(1)设到达C点速度为,C点到D点的时间为,则水平方向
竖直方向
解得
,
由A点到C点过程中,滑板克服滑道ABC做功为,根据动能定理有
解得
(2)设到达C点速度为,C点到E点的时间为,则竖直方向
E点速度关系为
解得
,
由A点到C点过程中,根据动能定理有
解得
36.(1)50m/s;(2)1.16105J;(3)1.42104N
【解析】
【分析】
【详解】
(1)石块平抛运动的高度
根据
解得
则初速度为
(2)根据动能定理可得
(3)石块圆周运动至最高点时,根据牛顿第二定律有
可得
方向向上
37.(1);(2)3m ;;(3),方向水平向右
【解析】
【详解】
(1)A沿弧形轨道下滑到水平轨道的过程中,机械能守恒有
mgh=
解得
v0=
(2)A与B碰撞的过程,动量守恒、机械能守恒,有
mv0=-mvA+mBvB
=
据题意有
vA=vB
解得
mB=3m
vA=
(3)则A对B的冲量大小为
IAB=3mvB=
方向水平向右.
38.(1)3m/s;(2)2150N,竖直向下;(3)3.55m
【解析】
【详解】
(1)运动员从A平抛至B的过程中,
在竖直方向有
①
在B点有
②
由①②得
③
(2)运动员在圆弧轨道做圆周运动到C处时,牛顿第二定律可得:
④
运动员从A到C的过程,由机械能守恒得:
⑤
联立③④⑤解得
由牛顿第三定律得:对轨道的压力为
N
方向竖直向下;
(3)运动员经过C点以后,由图可知:m,
设最远距离为x,则,由动能定理可得:
⑥
由⑤⑥代值解得
x=3.55m
答案第1页,共2页
答案第1页,共2页
一、单选题
1.木块在水平恒力F作用下,由静止开始在水平路面上前进S,随即撤去此恒力后又前进2S才停下来,设运动全过程中路面情况相同,则木块在运动中所获得的动能的最大值为( )
A. B. C.FS D.
2.李佳同学在学校秋季田径运动会上参加了高一组径赛项目的决赛,在终点冲刺时他的动能最接近( )
A. B. C. D.
3.如图,半圆形光滑轨道固定在水平地面上,半圆的直径与地面垂直,一小物块以速度v从轨道下端滑入轨道,并恰能从轨道上端水平飞出,则轨道半径为(重力加速度为g)( )
A. B. C. D.
4.如图所示,光滑轨道MO和ON底端对接,且,M、N两点高度相同.小球自M点由静止滚下,忽略小球经过O点时的能量损失,以v、x、a、分别表示小球的速度、位移、加速度和动能四个量的大小.下列图象中能正确反映小球自M点到N点运动过程的是
A. B. C. D.
5.如图所示,固定在竖直平面内的光滑圆管轨道ABCD,其A点与圆心等高,D点为最高点,今使质量为m的小球自A点正上方h高处由静止释放,且从A处进入圆管轨道并经过D点刚好落回A点,则下列说法中正确的是
A.只要小球就会落回到A点
B.当时小球一定过最高点D并落回到A点
C.当小球刚好落回到A点时,小球在D点所受的弹力大小为,方向向下
D.当小球刚好落回到A点时,小球在D点所受的弹力大小为,方向向上
6.下列物理量属于矢量的是( )
A.动能 B.功率 C.向心加速度 D.周期
7.战斗机以一定的水平初速度着陆甲板时,若飞机勾住阻拦索减速,飞机在甲板上滑行的距离将大大减小.着舰使用阻拦索时,下列说法正确的是( )
A.战斗机的动能变化量变大
B.战斗机的惯性减少得快
C.战斗机的加速度变大
D.战斗机的速度减少得多
8.物体在变力作用下沿水平方向做直线运动,物体质量,F随坐标的变化情况如图所示.若物体在坐标原点处由静止出发,不计一切摩擦.借鉴教科书中学习直线运动时由图象求位移的方法,结合其他所学知识,根据图示的图象,可求出物体运动到处时,速度大小为( )
A.
B.
C.
D.
9.如图甲所示,倾角为θ的斜面足够长,质量为m的小物块受沿斜面向上的拉力F作用,静止在斜面中点O处,现改变拉力F的大小 (方向始终沿斜面向上),物块由静止开始沿斜面向下运动,运动过程中物块的机械能E随离开O点的位移x变化关系如图乙所示,其中0-过程的为曲线过程的图线为直线,物块与斜面间动摩擦因数为.物块从开始运动到位移为的过程中
A.物块的加速度始终在减小
B.物块减少的机械能等于物块克服合力做的功
C.物块减少的机械能小于减少的重力势能
D.物块减少的机械能等于物块克服摩擦力做的功
10.质量为2kg的物体做直线运动,沿此直线作用于物体的外力与位移的关系如图所示,若物体的初速度为1m/s,则其8s末速度为( )
A.m/s B.m/s C.m/s D.m/s
11.抛出的铅球在空中的运动轨迹如图所示,、为轨迹上等高的两点,铅球可视为质点,空气阻力不计.用、、、分别表示铅球的速率、机械能、动能和重力瞬时功率的大小,用表示铅球在空中从运动到的时间,则下列图像中正确的是( )
A. B. C. D.
12.把一小球放在竖立的轻弹簧上,并把小球往下按至A的位置,如图甲所示。迅速松手后,弹簧把小球弹起,小球升至最高位置C(图丙),途中经过位置B时弹簧正好处于自由状态(图乙)。不计空气阻力,下列说法正确的是( )
A.小球从A运动到B的过程中,弹簧的弹性势能全都转化为小球的重力势能
B.小球从A运动到C的过程中,弹簧的弹性势能全都转化为小球的重力势能
C.小球从A运动到B的过程中,动能一直增大
D.小球从A运动到B的过程中,动能最大的位置为AB的中点
13.如图所示,表面光滑的固定斜面顶端安装一定滑轮,物块A、B用轻 绳连接并跨过滑轮(不计滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好静止.剪断轻绳后A下落、B沿斜面下滑,则从剪断轻绳到物块分别落地的过程中,两物块( )
A.落地时速度相同
B.运动时间相同
C.重力势能的变化量相同
D.重力的平均功率相同
14.一质点从t=0时刻开始做自由落体运动,E表示下落过程中的动能,x表示下落的位移,t表示下落的时间。下列图像中可能正确的是( )
A. B.
C. D.
15.如图为一发光轨道yoyo球结构,yoyo球具有磁性,可以紧贴铁质的轨道外侧做圆周运动,若不考虑球与轨道之间的摩擦,且yoyo球与轨道之间的磁力大小不变。则停止甩动yoyo球让其转动起来后( )
A.做的是匀速圆周运动
B.在最高点速度不能小于
C.在最高点对轨道的压力大于最低点对轨道的压力
D.由于有磁力作用,yoyo球运动过程中机械能不守恒
16.在“探究功与速度变化的关系”的实验中,可以得到橡皮筋对小车做的功W与小车获得的速度大小v之间的关系,下列关系正确的是( )
A.W∝v B.W∝v2 C. D.
17.如图所示,一弹簧下端系一物体,用手托着物体,使弹簧保持原长l0.现使物体缓缓地下降到平衡位置O,并保持静止。在此过程中,重力对物体做功的大小为Wg,弹簧的弹力对物体做功的大小We,手的支持力对物体做功的大小为W。则有( )
A.W=Wg B.W
18.如图,站在向右作匀加速直线运动的车厢内的人向前推车壁,下列说法正确的是
A.人对车的作用力仅是手的推力
B.车对人的摩擦力大于车对人的推力
C.因为人相对车没有动,所以合外力为零
D.该人对车做正功
19.如图,水从竖直放置的花洒喷出,落在水平地面上。某时刻从各喷口处水平喷出初速度相等的一小段水柱,在空中的运动都可视为平抛运动,则( )
A.各段水柱同时落地
B.各段水柱落地时的速度大小相等
C.从最低点喷出的水柱落地时的水平射程最大
D.从最高点喷出的水柱落地时的速度偏向角最大
二、多选题
20.如图所示,花样滑冰双人自由滑比赛时的情形,男运动员以自己为转动轴拉着女运动员做匀速圆周运动,若男运动员转速为30r/min,手臂与竖直方向夹角约为60°,女运动员质量是50kg,她触地冰鞋的线速度为4.7m/s,则下列说法正确的是( )
A.女运动员做圆周运动的加速度为
B.女运动员触地冰鞋做圆周运动的半径约为2m
C.男运动员手臂拉力约是850N
D.男运动员手臂拉力约是500N
21.排球课上小明同学练习垫球,现将质量为m的排球,以竖直向上垫起,由于空气阻力作用,排球上升时加速度大小为g,小明在原垫起点接住排球,排球在整个运动过程中受到的阻力大小恒定。关于排球的运动,下列说法正确的是( )
A.整个过程阻力不做功
B.整个过程克服阻力做
C.返回垫起点时重力的瞬时功率为
D.返回垫起点时重力的瞬时功率为
22.铅块质量为0.8kg,以初速度从下端滑上很长的斜面,斜面倾角为37°,铅块到达中途某点损失机械能,损失动能,只考虑斜面阻力,,,,则有( )
A.铅块以向上滑
B.铅块不可返回下端处,全程损失机械能
C.铅块与斜面摩擦系数为0.5
D.铅块可返回下端处,到下端剩余动能
23.如图所示,当小车向右加速运动时,物块M相对车厢静止于竖直车厢壁上,当车的加速度增大时( )
A.M对车厢壁的压力不变 B.M受静摩擦力增大
C.M受静摩擦力不变 D.M仍相对于车厢静止
24.关于下列实验的说法正确的是( )
A.在“探究加速度与力、质量的关系”实验中,需要平衡摩擦力
B.在“探究求合力的方法”实验中,两个分力与合力的标度一定要相同
C.在用橡皮筋做“探究功与速度变化的关系”实验时,可以求得做功的具体数值
D.在“验证机械能守恒定律”的实验中,可以用重力加速度计算重锤在某时刻的速度
三、实验题
25.某实验小组采用如图甲所示的实验装置来探究功与速度变化的关系。
(1)下列关于该实验的说法正确的是_______;
A.将木板一端垫高,使小车的重力沿斜面向下的分力与摩擦阻力平衡。方法是轻推小车,根据打点计时器打在纸带上的点是否均匀判断小车是否做匀速运动
B.测小车速度时,应选纸带上的点迹距离均匀增加的部分,也就是选小车做匀加速运动的部分
C.橡皮筋应选规格一样的。力对小车做的功以一条橡皮筋做的功为单位即可,不必计算出具体数值,而只是看第2次、第3次……实验中的是第1次的多少倍,简化数据的测量和处理
D.小车质量应小一些,使纸带上打的点少一些
(2)在正确操作的情况下,该小组某次所打的纸带如图乙所示。为了测量橡皮筋做功后小车获得的速度,应选用纸带上的_______(填“”“”或“”)段进行测量;若使用的交流电的频率为,则小车最终获得的速度是______(保留3位有效数字)。
(3)以为纵坐标,为横坐标,利用实验数据作出如图所示的图象,该图象为一条直线,说明_______。根据功与能的关系,动能的表达式中可能包含这个因子,分析实验结果的单位关系,与图线斜率有关的物理量应是_______。
(4)假设没有完全消除摩擦力和其他阻力,认为每次这些力都一样,则从理论上分析,下列图中正确反映关系的是_______。
A. B. C. D.
26.某实验小组要探究力对物体做功与物体获得速度的关系,选取的实验装置如图所示,实验主要步骤如下:
(1)实验时,为使小车只在橡皮筋作用下运动,在未连接橡皮筋时将木板的左端用小木块垫起,使木板倾斜合适的角度,打开打点计时器,轻推小车,得到的纸带应该是____填(“甲”或“乙”)
(2)使小车在一条橡皮筋的作用下由静止弹出,沿木板滑行,这时橡皮筋对小车做的功为W;
(3)再用完全相同的2条、3条……橡皮筋作用于小车,每次由静止释放小车时橡皮筋的______________(填写相应实验条件),使橡皮筋对小车做的功分别为2W、3W…
(4)分析打点计时器打出的纸带,分别求出小车每次获得的最大速度v1、v2、v3…
(5)作出W-v图像,则下列图像符合实际的是_______
27.用如图所示的装置做“探究动能定理”的实验时,下列说法正确的是__________.
A.为了平衡摩擦力,实验中可以将长木板的左端适当垫高,使小车在不挂橡皮筋时能拉着穿过打点计时器的纸带保持匀速运动
B.每次实验中橡皮筋的规格要相同,拉伸的长度要一样
C.可以通过改变小车的质量来改变拉力做功的数值
D.可以通过改变橡皮筋的条数改变拉力做功的数值
E.通过打点计时器打下的纸带来测定小车加速过程中获得的最大速度
F.实验中要先释放小车再接通打点计时器的电源
G.通过打点计时器打下的纸带来测定小车加速过程中获得的平均速度
四、解答题
28.从离地面h=80m高处水平抛出的物体,着地时的水平位移为x=20m,求:
(1)运动时间;
(2)初速度大小;
(3)落地时速度大小及它与水平方向夹角的正切;
(4)在空中运动的第2s内速度的变化△v.
29.追寻守恒量是物理学的重要研究内容,在高中阶段我们探索守恒量时,除了实验手段,也常借助已有理论来进行分析。已知重力加速度为g。供暖系统、自来水系统都是通过管道运送液体的。管内液体稳定流动时具有这样的特点:①管内各处液体体积无法压缩且密度均相同;②管内各处液体流速不随时间改变。如图所示,选取横截面C和横截面D之间的液体为研究对象,当C处液体流动很小一段距离,到达时,D处液体正好流动到处。已知液体密度为,C处的压强为、流速为、高度为,D处的压强为、流速为、高度为,C处管道半径为R,C与间距离为d,且R、d均远远小于。不计管道对液体的阻力,不考虑液体的黏滞性。在C、D间的液体流动至、的过程中
(1)求横截面C左侧液体对研究对象所做的功;
(2)求重力对研究对象所做的功;
(3)研究表明,可运用动能定理对C、D间的液体进行分析。请依据动能定理探索压强p、流速u、高度h是否也存在着某种守恒的关系。若存在,请写出关系式;若不存在,请说明理由。
30.如图所示,水平桌面上的轻质弹簧左端固定,右端与静止在O点质量为m=1kg的小物块接触而不连接,此时弹簧无形变.现对小物块施加F =" 10" N水平向左的恒力,使其由静止开始向左运动.小物块在向左运动到A点前某处速度最大时,弹簧的弹力为 6 N,运动到A点时撤去推力F,小物块最终运动到B点静止.图中OA =" 0.8" m,OB =" 0.2" m,重力加速度g =" 10" m/s2.求小物块:
(1)与桌面间的动摩擦因数μ;
(2)向右运动过程中经过O点的速度;
(3)向左运动的过程中弹簧的最大压缩量.
31.某游乐场的滑梯可以简化为如图所示竖直面内的ABCD轨道,AB为长L=5m、倾角的斜轨,BC为水平轨道,CD为半径R=14m的圆弧轨道。轨道AB段粗糙,其余各段均光滑,一小孩(可视为质点)从A点以初速度v0=3m/s下滑,沿轨道运动到C点时的速度vC=7m/s,全程不滑离轨道(不计经过B点时的能量损失)。已知该小孩的质量m=20kg,取sin37°=0.6,cos37°=0.8,不计空气阻力,设最大静摩擦力等于滑动摩擦力。求:
(1)小孩沿轨道AB运动过程中重力所做的功;
(2)该小孩第一次经过圆弧C点时,对圆弧轨道的压力FN;
(3)该小孩与AB轨道间的动摩擦因数;
(4)该小孩在轨道AB上运动的总路程s。
32.某同学用锤子将一个小铁钉钉进墙壁中.钉子进入墙壁过程中,所受阻力f与钉进深度x间的关系如图所示.铁钉重力可以忽略不计,则:
(1) 该同学第一次敲击铁钉,发现铁钉进入深度为,求该过程锤子对铁钉做的功W0;
(2) 若每一次敲击,锤子对铁钉做功恒为W0,则敲击两次,铁钉进入的深度为多少;
(3) 在(2)的条件下,若要使铁钉进入深度为4x0,应敲击铁钉几次.
33.在光滑的水平面上放着物体A和小车B,如图所示,小车长L=2m,M=4kg,A的质量m=1kg,μAB=0.2,假设最大静摩擦力等于滑动摩擦力,求:(g取10m/s2)
(1)若加在小车上的力F=5N,在这种情况下,在2s时间内F对车做功是多少?摩擦力对A做功多少?小车动能增加多少?
(2)若加在小车上的力F=12N,在这种情况下,在2s时间内F对车做功是多少?摩擦力对A做功多少?小车动能增加多少?
34.如图所示,在倾角θ=30°的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量均为m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现开始用一沿斜面方向的力F拉物块A使之向上匀加速运动,当物块B刚要离开C时F的大小恰为2mg.问:
(1)从F开始作用到物块B刚要离开C的过程中弹簧弹力对物块A做的功;
(2)物块B刚要离开C时物块A的动能;
(3)从F开始作用到物块B刚要离开C的过程中力F做的功.
35.第24届冬奥会将于2022年由北京和张家口两个城市联合举办,跳台滑雪是其中最具观赏性的项目之一,其空中翻转动作优美,深受观众喜爱。某滑道示意图如图所示,长直助滑道AB与光滑圆弧形滑道BC相切于B点,且AB与B、C两点所在水平面的夹角,助滑道AB长L=90m。圆弧滑道BC与水平安全平台CD连接,CD长x=38.4m。平台CD与曲线着陆坡DE连接,D、E两点高度差为35m。着陆坡DE下端衔接一段圆心角的圆弧轨道,圆弧轨道最低点与水平终点区FG相切。质量m=80kg(含滑板等装备)的运动员(可视为质点)从A处由静止开始自由下滑(运动员不做功),经C点飞起,恰好从D点进入曲线着陆坡DE。重力加速度,运动员在空中运动过程中可视为质点,忽略运动过程中空气的作用。
(1)滑板克服滑道AB阻力做功为多少;
(2)某次试赛中,该运动员从A处由静止开始加速下滑(运动员做功),恰从E点沿切线进入圆弧轨道,实现完美一跃。求此过程中运动员做的功。
36.如图甲所示,在公元1267-~1273年闻名于世的“襄阳炮”其实是一种大型抛石机。将石块放在长臂一端的石篮中,在短臂端挂上重物。发射前将长臂端往下拉至地面,然后突然松开,石袋中的石块过最高点时就被拋出。现将其简化为图乙所示。将一质量m=80kg的可视为质点的石块装在长m的长臂末端的石篮中,初始时长臂与水平面成30°,松开后,长臂转至竖直位置时石块被水平抛出落在水平地面上。石块落地点与O点的水平距离s=100m。忽略长臂、短臂和石袋的质量,不计空气阻力和所有摩擦,g=10m/s2,求:
(1)石块水平抛出时的初速度v0;
(2)石块从A到最高点的过程中石篮对石块做功W;
(3)石块圆周运动至最高点时,石块对石篮的作用力F。
37.如图所示,一弧形轨道与足够长的水平轨道平滑连接,水平轨道上静止一小球B。从弧形轨道上距离水平轨道高h处由静止释放一质量为m的小球A,A球沿轨道下滑后与B球发生弹性正碰,碰后A球被弹回,A球重新下滑到水平轨道后,与B球间的距离保持不变。所有接触面均光滑。求:
(1)碰撞前瞬间A球的速度大小;
(2)B球的质量和碰撞结束时A球的速度大小;
(3)碰撞结束时A对B的冲量。
38.滑板运动是青少年喜爱的一项活动。如图甲所示,滑板运动员以某一初速度从A点水平离开h=0.8m高的平台,运动员(连同滑板)恰好能无碰撞的从B点沿圆弧切线进入竖直光滑圆弧轨道,然后由C点滑上涂有特殊材料的水平面,水平面与滑板间的动摩擦因数从C点起按图乙规律变化,已知圆弧与水平面相切于C点,B、C为圆弧的两端点。圆弧轨道的半径R=1m;O为圆心,圆弧对应的圆心角=53°,已知,,,不计空气阻力,运动员(连同滑板)质量m=50kg,可视为质点,试求:
(1)运动员(连同滑板)离开平台时的初速度v0;
(2)运动员(连同滑板)通过圆弧轨道最低点对轨道的压力;
(3)运动员(连同滑板)在水平面上滑行的最大距离。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【详解】
对全程由动能定理得:Fs-f 3s=0,则:f=F,由题意可知,当拉力撤销的时候,木块获得最大动能:由动能定理可知:Ekm=Fs-fs=Fs-Fs=Fs;故选D.
2.B
【解析】
【分析】
【详解】
假设李佳同学质量为60kg,重点冲刺速度为10m/s,则动能为
故选B。
3.B
【解析】
【详解】
设半圆的半径为R,从轨道下端滑入到上端过程中,根据动能定理得
在最高点,根据牛顿第二定律有
mg=
解得轨道半径R=.
A.轨道半径为,与分析不一致,故A错误;
B.轨道半径为,与分析相一致,故B正确;
C.轨道半径为,与分析不一致,故C错误;
D.轨道半径为,与分析不一致,故D错误.
4.B
【解析】
【详解】
因为在MO和NO段的平均速度相等,位移之比为1:2,则时间之比为1:2;对于速度时间图线,小球运动过程中,在两个斜面上都沿斜面做匀变速运动;对于位移时间图线,由于在两个斜面上都是匀变速运动,根据位移时间关系公式,可知位移时间图象是曲线,该图线错误,故A错误;做匀变速直线运动,速度先增加后减小,根据速度时间关系公式,可知两段运动过程中的图都是直线,且MO段图线的斜率绝对值大于ON段图线斜率的绝对值,该图线正确,故B正确;对于加速度时间图线,加速度的大小与斜面的倾角大小有关,倾角确定,加速度大小确定,该图线错误,故C错误;对于动能时间图线,速度与时间是一次函数关系,动能与速度的二次方成正比,故动能与时间也是二次函数关系,该图线错误,故D错误.故选B.
点睛:研究两个物理量之间的关系图线,关键是根据物理规律得出两个量的表达式,从而分析判断,这是解决图象题的常用方法.
5.D
【解析】
【分析】
【详解】
A.小球自A点正上方h高处由静止释放到A点,有机械能守恒得
从A点到D点,机械能守恒
从D点到A点,小球做平抛运动
以上几个式子联立,解得
所以当时小球一定过最高点D并落回到A点,AB错误;
CD.在D点,受力分析有
解得
且方向向上,C错误,D正确。
故选D。
6.C
【解析】
【详解】
矢量既有大小又有方向,标量只有大小没有方向;
ABD.动能、功率、周期,都只有大小,没有方向,为标量,ABD错误;
C.向心加速度既有大小又有方向,为矢量,C正确。
故选C。
7.C
【解析】
【详解】
AD. 两种情况下,战斗机的初末动能相同,动能的变化量相同,速度减小的一样多,故A项错误,D错误;
B. 惯性只与物体的质量有关,惯性不变,故B项错误;
C. 根据速度位移公式可知,舰使用阻拦索时滑行距离减小,战斗机的加速度变大,故C项正确;
8.B
【解析】
【详解】
根据图象求位移的方法可知图象的面积代表力做的功,所以全程动能定理得:,且联立解得:,ACD错误B正确.
9.C
【解析】
【分析】
【详解】
A.由图可知,物块向下运动的过程中,其中O~x1过程的图线为曲线,斜率逐渐减小,而斜率
联立可知
斜率减小,则减小,物块受到的合外力
不一定减小,由牛顿第二定律可知,物块的加速度不一定减小;在x1~x2过程的图线为直线,k不变,则物块的加速度不变,A错误;
BD.物块向下运动的过程中,重力、拉力与摩擦力做功,物块减少的机械能等于拉力与摩擦力做功,不等于物块克服合力做的功,BD错误;
C.物块由静止开始沿斜面向下运动,由动能定理可知
重力势能减小量等于重力功WG,机械能的减小量等于 ,所以物块减少的机械能小于减少的重力势能,C正确。
故选C。
10.B
【解析】
【详解】
外力与位移图象与坐标轴围成的面积表示外力所做的功,由图可知
根据动能定理得
解得
故选B。
11.D
【解析】
【详解】
AB.铅球做斜上抛运动,机械能守恒,重力势能先增加后减小,故动能先减小后增加,速度先减小后增加,故AB错误;
C.以初始位置为零势能面,抛出时速度方向速度为,铅球的机械能守恒,则
故图象为抛物线,故C错误;
D.速度的水平分量不变,竖直分量先减小到零,后反向增加,故根据
重力的功率先均匀减小后均匀增加,故D正确;
故选D。
12.B
【解析】
【详解】
A.小球从A运动到B的过程中,因小球在B点具有速度,所以弹簧的弹性势能一部分转化为小球的重力势能,还有一部分转化为小球的动能,故A错误;
B.小球从A运动到C的过程中,由于小球在C点的速度为零,则弹簧的弹性势能全都转化为小球的重力势能,故B正确;
C.小球从A运动到B的过程中,先向上作加速运动,后作减速运动,所以其动能不是一直增大,而是先增大后减小,故C错误;
D.小球从A运动到B的过程中,动能最大的位置为小球的重力等于弹簧的弹力时的位置,而不一定是AB的中点位置,故D错误。
故选B。
13.D
【解析】
【详解】
剪断轻绳后A自由下落,B沿斜面下滑,AB都只有重力做功,根据机械能守恒定律得,得,可知两个物体落地速度大小相等,但方向不同,所以落地速度不同,A错误;根据牛顿第二定律可知B的加速度为,即加速度不同.对A,由,得;对B,由,则得,可知运动时间不同,重力的平均功率为,,由于,故,B错误D正确;未间断细绳前,,故两者的质量不同,下落高度相等,故重力势能变化量不同,C错误.
14.C
【解析】
【分析】
【详解】
AB.根据自由落体运动运动规律有
则动能
由数学知识知,图像应为开口向上的抛物线,故AB错误;
CD.根据动能定理,有
由数学知识知,图像为一条过原点的倾斜直线,故C正确,D错误。
故选C。
15.C
【解析】
【分析】
【详解】
A.停止甩动yoyo球让其转动起来后重力对球做功,则yoyo球做变速圆周运动,故A错误;
B.yoyo球在最高点时重力与磁力的合力和弹力等大反向时,球的速度为0,即在最高点最小速度为0,故B错误;
C.在最高点由牛顿第二定律有
在最低点由牛顿第二定律有
从最高点到最低点由动能定理可知
得
则在最高点对轨道的压力大于最低点对轨道的压力,故C正确;
D.由于磁力方向始终与速度方向垂直,则磁力不做功,球在运动过程中只有重力做功,则机械能守恒,故D错误。
故选C。
16.B
【解析】
【详解】
小车在橡皮筋拉力作用下由静止开始运动,初动能为零,由动能定理可知
物体的质量一定,则
故选B。
17.B
【解析】
【详解】
用手托着物体,使物体缓缓地下降到平衡位置O,在此过程中物体状态不变,动能变化量为0,根据动能定理得
变形得
故选B。
18.B
【解析】
【详解】
对人分析可知,人受重力、车向左的弹力以及地面向右的摩擦力;故人对车有向左的摩擦力和推力;故A错误;对人分析由牛顿第二定律可知,人受到的合力向右,故摩擦力大于车对人的推力;故B正确;C错误;由于车对人的合力向右,则可知人对车的合力一定向左,则由功的公式可知,人对车做负功;故D错误;故选B.
【点睛】
此题涉及到牛顿第二定律的应用和力的作用的相互性,解决此类题目要结合作用力和反作用力考虑,同时注意功的分析和判断方法.
19.D
【解析】
【详解】
A.根据平抛运动公式
解得
由于各段水柱的高度不一样,所以不能同时落地,故A错误;
B.落地时竖直方向的分速度为
水平方向的分速度为
所以落地速度大小为
由于高度不相等,所以各段水柱落地时的速度大小也不相等。故B错误;
C.水平位移为
故高度最大的水柱水平位移最大。故C错误;
D.设水柱落地时的速度偏向角为,则
根据公式可知,高度越大的水柱,下落的时间越长,就越大,故D正确。
故选D。
20.AC
【解析】
【详解】
A.女运动员做圆周运动的角速度等于男运动员转动的角速度,则
rad/s
A正确;
B.根据:
得:m,B错误;
CD.拉力沿水平方向上的分力提供向心力,则有:
解得,C正确,D错误。
故选AC。
【点睛】
关键是知道两运动员运动的角速度相同,然后根据转速的大小得出圆周运动的角速度,根据拉力沿水平方向上的分力提供向心力。
21.BD
【解析】
【分析】
【详解】
AB.排球上升过程,根据牛顿第二定律,有
带入数据,可得
该过程排球的位移大小为
则整个运动过程中,阻力做功为
带入数据,可得
所以整个过程克服阻力做功为
故A错误;B正确;
CD.设返回垫起点时排球速度为,整个过程中由动能定理,有
整理,可得
所以返回垫起点时重力的瞬时功率为
故C错误;D正确。
故选BD。
22.AD
【解析】
【详解】
BC.向上减速运动重力势能增加,动能减小,损失的机械能为摩擦生热,根据能量守恒可得
联立可解得
上升到某点的位移为,则有
解得
由于,则铅块可返回下端。BC错误;
A.铅块受沿斜面向下的摩擦力和沿斜面向下重力的分力,由牛顿第二定律得
解得
A正确;
D.上升到最高点时的位移为
返回下端时,根据动能定理可得
解得
D正确。
故选AD。
23.CD
【解析】
【详解】
对物块M,水平方向
FN=ma
竖直方向
f=mg
则当车的加速度增大时M对车厢壁的压力增大,最大静摩擦力变大,则M仍相对于车厢静止,M受静摩擦力不变。
故选CD。
24.AB
【解析】
【详解】
A、在“探究加速度与质量、外力之间的关系”实验中,需要平衡摩擦力,故A正确;
B、在“探究求合力的方法”实验中,两个分力与合力的标度一定要相同,故B正确;
C、实验时,每次保持橡皮筋的形变量一定,当有n根相同橡皮筋并系在小车上时,n根相同橡皮筋对小车做的功就等于系一根橡皮筋时对小车做的功的n倍,这个设计很巧妙地解决了直接去测量力和计算功的困难,故实验中不需要测出一条橡皮筋对小车做功W的数值,故C错误;
D、在验证机械能守恒的实验中,由于存在阻力物体实际下落的加速度小于重力加速度,不可以用重力加速度计算重锤在某时刻的速度,应该运用某段时间内的平均速度等于中间时刻的瞬时速度,故D错误;
故选AB.
25. AC##CA BC 0.686 合外力对小车做的功,与小车的速度的平方成正比 小车的质量 B
【解析】
【详解】
(1)[1]A.小车与木板间有摩擦,将木板一端垫高,平衡摩擦力,轻推小车打点计时器在纸带上的点迹均匀小车做匀速运动,故A正确;
B.测小车速度时,应选纸带上的点迹均匀的部分进行计算,故B错误;
C.因为此实验改变做功是通过改变橡皮筋条数来实现的,则只要保证小车质量不变即可,不必测小车质量,也不必测功的具体值,只是用W、2W、3W等表示,简化数据的测量和处理。故C正确;
D.小车质量不能太大或太小,保证纸带上的点迹不要过于密集或稀疏,方便处理数据,故D错误。
故选AC。
(2)[2]测小车速度时,应选纸带上的点迹均匀的部分进行计算,故应选BC段;
[3]小车最终获得的速度是
(3)[4]合外力对小车做的功,与小车的速度的平方成正比;
[5]由图可得v随W变化的表达式为v2=kW,由等式两端的物理量单位可知,左侧单位为,右侧单位为J,所以k的单位为
所以与图线斜率有关的物理量应是小车的质量。
(4)[6]若没有完全消除摩擦力和其他阻力,橡皮筋对小车的功有部分用于克服阻力做功,没有全部转化为小车的动能,故B正确。
故选B。
26. 乙 伸长量(或形变量、长度等)都相同 D
【解析】
【详解】
(1)[1]平衡摩擦力后,小车应做匀速运动,所以纸带应该是图乙;
(2)[2]橡皮条拉力是变力,采用倍增法增加功;即使小车在一条橡皮筋的作用下由静止弹出,这时橡皮筋对小车做的功为W;再用完全相同的2条、3条…橡皮筋作用于小车,每次由静止释放小车时橡皮筋的伸长量都相同,使橡皮筋对小车做的功分别为2W、3 W…
(5)[3]功与速度的平方相对应,所以图象应为D。
27.ABDE
【解析】
【详解】
A、小车在水平面运动时,由于受到摩擦阻力导致小车速度在变化,所以适当倾斜以平衡摩擦力,小车所能获得动能完全来于橡皮筋做的功,所以实验中可以将长木板的左端适当垫高,使小车在不挂橡皮筋时能拉着穿过打点计时器的纸带保持匀速运动,故A正确;
B、实验中每根橡皮筋做功均是一样的,所以所用橡皮筋必须相同,且伸长的长度也相同,故B正确;
C、是通过改变橡皮筋的条数来改变拉力做功的数值,故C错误;
D、每次实验时橡皮筋伸长的长度都要一致,则一根做功记为W,两根则为2W,可以通过改变橡皮筋的条数改变拉力做功的数值,故D正确;
F、只要使用打点计时器的实验,都是先接通电源后释放纸带,故F错误;
EG、由于小车在橡皮筋的作用下而运动,橡皮筋对小车做的功与使小车能获得的最大速度有关,故E正确, G错误;
故选ABDE.
28.(1)4s (2)5m/s(3)20.6m/s; 8(4)10m/s
【解析】
【详解】
试题分析:(1)运动时间
(2)初速度大小
(3)落地时竖直速度大小:vy=gt=40m/s
落地的速度:
落地的速度与水平方向夹角的正切;
(4)在空中运动的第2s内速度的变化△v=gt=10×2=20m/s.
考点:平抛运动
【名师点睛】本题就是对平抛运动规律的直接考查,掌握住平抛运动的规律就能轻松解决;要知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.
29.(1);(2);(3)
【解析】
【详解】
(1)横截面C左侧液体对研究对象所做的功
(2)C、D间液体流动至、间,可等效为、D间液体位置不变,C、间液体流动至D、间。C、间液体质量
重力对研究对象所做的功
(3)在相同的时间内,流过C处截面水的体积与流过D处截面水的体积相同。由C,间液体体积
可知
设D处管道面积为,D、间距离为x,则D、间液体体积
横截面D右侧液体对研究对象所做的功
由动能定理,合外力做功
即
整理得
所以压强、流速、高度是满足守恒的关系,即
为守恒量。
30.(1)0.4(2)(3)0.9m
【解析】
【详解】
试题分析:(1)小物块速度达到最大时,加速度为零.
(2)设向右运动通过O点时的速度为v0,由动能定理列出:
解得
(3)设撤去F推力后,小物块继续向左运动x的距离,弹簧的压缩量最大值为.取小物块运动的全过程,根据动能定理列出:
则
考点:动能定理;牛顿定律.
31.(1)600J;(2)270N,方向向下;(3)0.25;(4)17.25m
【解析】
【分析】
【详解】
(1)小孩沿轨道AB运动过程中重力所做的功为
(2)小孩第一次经过圆弧C点时,根据牛顿第二定律有
代入数据求得
FN=270N
根据牛顿第三定律,小孩对轨道的压力为270N,方向向下
(3)小孩从A点下滑,沿轨道运动到C点,根据动能定理有
代入数据求得
(4)由于
小孩从A点下滑,沿轨道运动最终将停止在水平BC段,根据动能定理有
代入数据求得
s=17.25m
32.(1) (2) (3)28次
【解析】
【详解】
(1) 该同学第一次敲击铁钉,发现铁钉进入深度为,如图知
该过程锤子对铁钉做的功
(2) 敲击两次,铁钉进入的深度为x,根据题意知x小于x0,此时
则有:
解得
(3) 当铁钉进入深度为x0时,摩擦力等于f0,此时需要做功为:
铁钉从x0到4x0过程中,需要做功为:
故要使铁钉进入深度为4x0,应敲击铁钉24+4=28次
33.(1)10J,2J,8J(2)60J,8J,50J
【解析】
【详解】
设A和B以共同加速度运动时F的最大值为F0,根据牛顿第二定律,对A、B整体有
对A单独有
解得
(1)当F=5N
AB间的摩擦力大小为
f=ma=1N
F对车做功
WF=Fx=10J
摩擦力对A做功
Wf=fx=2J
根据动能定理可知,合外力对车做功等于其动能增量,即
ΔEk=(F-f)x=8J
(2)当F=12N>F0时,A、B将出现相对滑动,此时A的加速度大小为
aA=a0=2m/s2
B的加速度大小为
在2s时间内A的位移大小为
B的位移大小为
AB间的摩擦力大小为
F对车做功
WF′=FxB=60J
摩擦力对A做功
Wf′=f′xA=8J
同(1)理可知小车动能增量为
ΔEk′=(F-f′)xB=50J
34.(1)0(2)(3)
【解析】
【详解】
(1)(2)令x1表示未加F时弹簧的压缩量,由胡克定律和牛顿定律可知:
mgsin30°=kx1
令x2表示B 刚要离开C时弹簧的伸长量,a表示此时A 的加速度,由胡克定律和牛顿定律可知:
kx2=mgsin30°
F-mgsin30°-kx2=ma
将F=2mg和θ=30°代入以上各式,解得:a=g
由x1+x2=at2
解得:
物块B刚要离开C时,物块A的速度为:v=at=g
故动能为:
此时弹簧的伸长量和F开始作用时的压缩量相同,弹簧的弹性势能改变量为零,故弹簧弹力做功为零;
(3)由动能定理得:
WF-mg(x1+x2)sin30°=mv2
解得:
35.(1)27200J;(2)20000J
【解析】
【分析】
【详解】
(1)设到达C点速度为,C点到D点的时间为,则水平方向
竖直方向
解得
,
由A点到C点过程中,滑板克服滑道ABC做功为,根据动能定理有
解得
(2)设到达C点速度为,C点到E点的时间为,则竖直方向
E点速度关系为
解得
,
由A点到C点过程中,根据动能定理有
解得
36.(1)50m/s;(2)1.16105J;(3)1.42104N
【解析】
【分析】
【详解】
(1)石块平抛运动的高度
根据
解得
则初速度为
(2)根据动能定理可得
(3)石块圆周运动至最高点时,根据牛顿第二定律有
可得
方向向上
37.(1);(2)3m ;;(3),方向水平向右
【解析】
【详解】
(1)A沿弧形轨道下滑到水平轨道的过程中,机械能守恒有
mgh=
解得
v0=
(2)A与B碰撞的过程,动量守恒、机械能守恒,有
mv0=-mvA+mBvB
=
据题意有
vA=vB
解得
mB=3m
vA=
(3)则A对B的冲量大小为
IAB=3mvB=
方向水平向右.
38.(1)3m/s;(2)2150N,竖直向下;(3)3.55m
【解析】
【详解】
(1)运动员从A平抛至B的过程中,
在竖直方向有
①
在B点有
②
由①②得
③
(2)运动员在圆弧轨道做圆周运动到C处时,牛顿第二定律可得:
④
运动员从A到C的过程,由机械能守恒得:
⑤
联立③④⑤解得
由牛顿第三定律得:对轨道的压力为
N
方向竖直向下;
(3)运动员经过C点以后,由图可知:m,
设最远距离为x,则,由动能定理可得:
⑥
由⑤⑥代值解得
x=3.55m
答案第1页,共2页
答案第1页,共2页
