高中物理人教版必修第二册第八章机械能守恒定律4机械能守恒定律提升练习(word版含答案)
文档属性
| 名称 | 高中物理人教版必修第二册第八章机械能守恒定律4机械能守恒定律提升练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 449.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-15 00:00:00 | ||
图片预览



文档简介
2019人教版必修第二册 第八章 机械能守恒定律 4 机械能守恒定律 提升练习
一、单选题
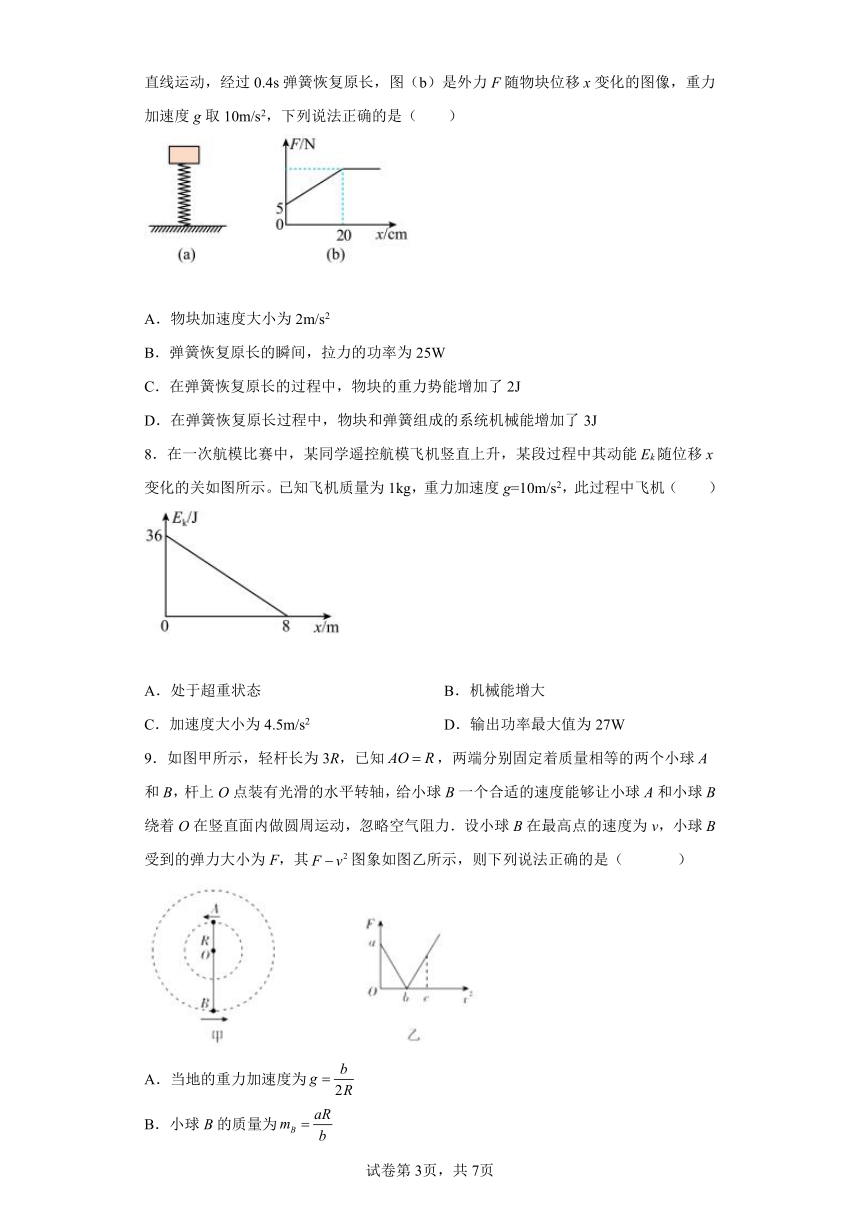
1.如图甲所示的“抓娃娃机”是老少皆宜的一种娱乐工具.若抓小熊的爪子有四个抓脚,某次抓小熊简化为如图乙所示(只画了左、右两个抓脚,前、后两个没画),其中一段过程如下:当小熊(可视为质点)被爪子夹紧,爪子通过轻绳悬挂在小环上,小环套在水平光滑细杆上,小熊质量为,到小环的距离为,小熊与每个抓脚间的最大静摩擦力均为.小环和小熊以速度向右匀速运动,小环碰到杆上的钉子后立刻停止,小熊向上摆动.整个过程中,小熊在爪子中没有滑动.小环和爪子的质量均不计,重力加速度为.下列说法正确的是( )
A.小熊向右匀速运动时,绳中的乙张力等于
B.小环碰到钉子时,绳中的张力大于
C.小熊上升的最大高度为
D.速度不能超过
2.如图所示,卷扬机的绳索通过定滑轮用力F拉位于粗糙斜面上的木箱,使之沿斜面加速向上移动.在移动过程中,下列说法中正确的是( )
A.木箱克服重力所做的功等于木箱机械能的增加
B.F对木箱做的功等于木箱增加的动能与木箱克服摩擦力所做的功之和
C.F对木箱做的功等于木箱克服摩擦力和克服重力所做的功之和
D.F对木箱做的功等于木箱增加的机械能与木箱克服摩擦力做的功之和
3.爱因斯坦说:“伽利略(Galileo galilei,1564﹣1642)的发现以及他所应用的科学推理方法,是人类思想史上最伟大的成就之一,标志着物理学的真正开端.”在科学史上,伽利略享有“近代科学方法论的奠基人”的美誉.根据你对物理学的学习和对伽利略的了解,他的物理思想方法的研究顺序是( )
A.提出假说,数学推理,实验验证,合理外推
B.数学推理,实验验证,合理外推,提出假说
C.实验验证,合理外推,提出假说,数学推理
D.合理外推,提出假说,数学推理,实验验证
4.在伽利略的斜面实验中,小球从一个斜面的某一高度由静止滑下,并运动到另一个斜面的同一高度,小球好像“记得”自己的起始高度,或与高度相关的某个量。“记得”并不是物理学的语言。后来的物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做( )
A.弹力 B.势能 C.速度 D.能量
5.下列说法正确的是( )
A.动量大的物体,它的动能一定也大
B.只要系统内存在摩擦力,系统动量就不可能守恒
C.一对相互作用力所做功的代数和一定为零
D.除重力做功外,其他力不做功,物体的机械能一定守恒
二、多选题
6.如图所示,细线的一端固定于O点,另一端系一小球,在水平拉力F作用下,小球缓慢地在竖直平面内由A点运动到B点的过程中( )
A.拉力F逐渐增大 B.拉力F对小球做正功
C.细绳对小球做负功 D.小球的机械能保持守恒
7.如图(a)所示,竖直放置的轻弹簧下端固定在地面上,上端与质量为m的物块相连(不拴接),初始时处于静止状态。现对物块施加竖直向上的外力F,使物块做匀加速直线运动,经过0.4s弹簧恢复原长,图(b)是外力F随物块位移x变化的图像,重力加速度g取10m/s2,下列说法正确的是( )
A.物块加速度大小为2m/s2
B.弹簧恢复原长的瞬间,拉力的功率为25W
C.在弹簧恢复原长的过程中,物块的重力势能增加了2J
D.在弹簧恢复原长过程中,物块和弹簧组成的系统机械能增加了3J
8.在一次航模比赛中,某同学遥控航模飞机竖直上升,某段过程中其动能Ek随位移x变化的关如图所示。已知飞机质量为1kg,重力加速度g=10m/s2,此过程中飞机( )
A.处于超重状态 B.机械能增大
C.加速度大小为4.5m/s2 D.输出功率最大值为27W
9.如图甲所示,轻杆长为3R,已知,两端分别固定着质量相等的两个小球A和B,杆上O点装有光滑的水平转轴,给小球B一个合适的速度能够让小球A和小球B绕着O在竖直面内做圆周运动,忽略空气阻力.设小球B在最高点的速度为v,小球B受到的弹力大小为F,其图象如图乙所示,则下列说法正确的是( )
A.当地的重力加速度为
B.小球B的质量为
C.由图乙分析可得到小球A转到最高点时的最小速度为
D.若,当小球A转到最高点时受到的弹力有可能为零
10.2021年6月17日,神舟十二号载人飞船与天和核心舱完成对接,航天员聂海胜,刘伯明、汤洪波进入天和核心舱,标志着中国人首次进入了自己的空间站。对接过程如图所示,天和核心舱处于半径为的圆轨道Ⅲ,神舟十二号飞船处于半径为的圆轨道Ⅰ,运行周期为,通过变轨操作后,沿椭圆轨道Ⅱ运动到处与天和核心舱对接。则神舟十二号飞船( )
A.需要加速才能由轨道Ⅰ进入轨道Ⅱ
B.沿轨道Ⅰ运行的周期大于天和核心舱沿轨道Ⅲ运行的周期
C.沿轨道Ⅱ运动到对接点过程中,速度不断增大
D.沿轨道Ⅱ运行的周期为
三、解答题
11.如图所示,倾角θ=30°的斜面上的P点距水平面高h=0.2m,光滑滑块A自P点由静止释放,同时滑块B自水平面上的Q点以速度v0=5m/s向右运动,已知B与水平面间的动摩擦因数μ=0.2,滑块A释放后经过t=1s在水平面上刚好与滑块B相遇。假设滑块A 滑过O点时机械能不损失。g取10m/s2,两滑块均可视为质点。求Q点与斜面底端O点的距离。
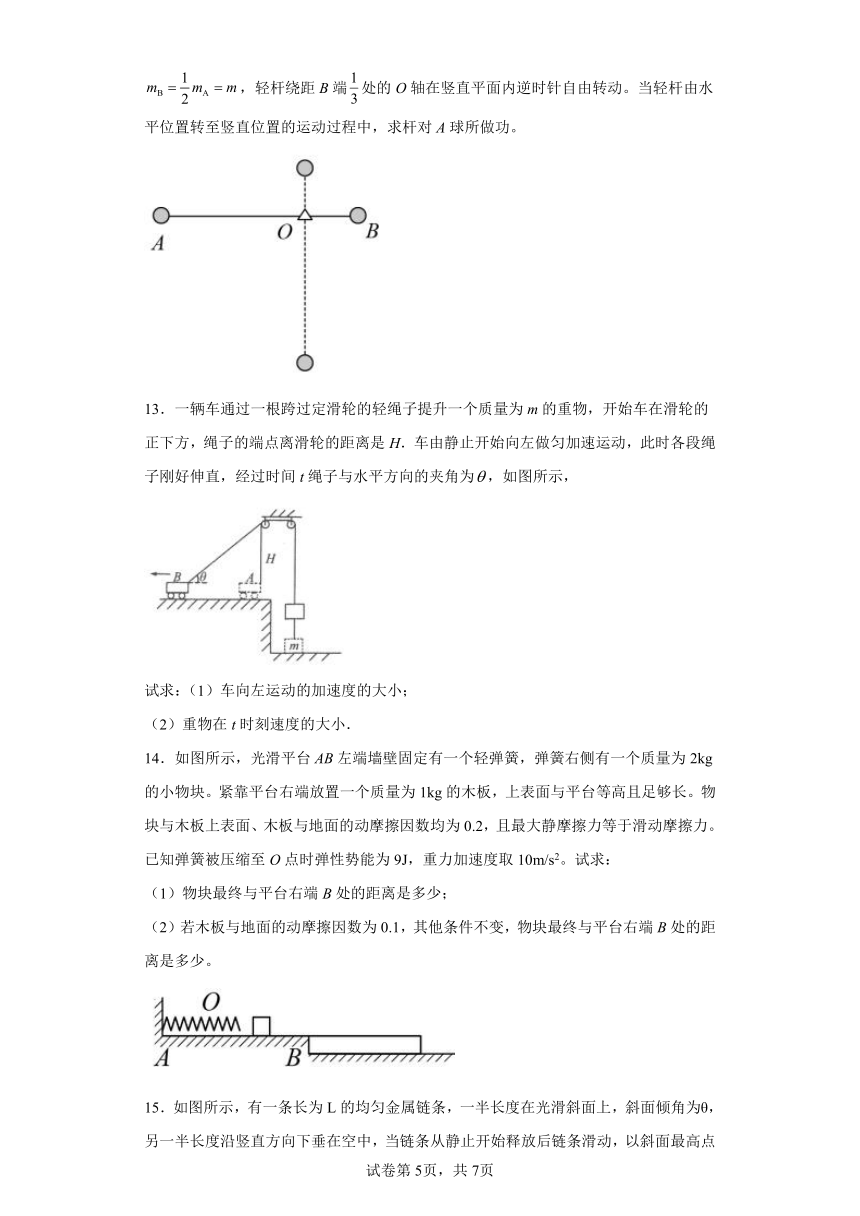
12.如图所示,轻杆AB长l,两端各连接一个小球(可视为质点),两小球质量关系为,轻杆绕距B端处的O轴在竖直平面内逆时针自由转动。当轻杆由水平位置转至竖直位置的运动过程中,求杆对A球所做功。
13.一辆车通过一根跨过定滑轮的轻绳子提升一个质量为m的重物,开始车在滑轮的正下方,绳子的端点离滑轮的距离是H.车由静止开始向左做匀加速运动,此时各段绳子刚好伸直,经过时间t绳子与水平方向的夹角为,如图所示,
试求:(1)车向左运动的加速度的大小;
(2)重物在t时刻速度的大小.
14.如图所示,光滑平台AB左端墙壁固定有一个轻弹簧,弹簧右侧有一个质量为2kg的小物块。紧靠平台右端放置一个质量为1kg的木板,上表面与平台等高且足够长。物块与木板上表面、木板与地面的动摩擦因数均为0.2,且最大静摩擦力等于滑动摩擦力。已知弹簧被压缩至O点时弹性势能为9J,重力加速度取10m/s2。试求:
(1)物块最终与平台右端B处的距离是多少;
(2)若木板与地面的动摩擦因数为0.1,其他条件不变,物块最终与平台右端B处的距离是多少。
15.如图所示,有一条长为L的均匀金属链条,一半长度在光滑斜面上,斜面倾角为θ,另一半长度沿竖直方向下垂在空中,当链条从静止开始释放后链条滑动,以斜面最高点为重力势能的零点,则:
(1)开始时和链条刚好从右侧全部滑出斜面时重力势能各是多大?
(2)重力在此过程中做了多少功?
16.如图所示,光滑水平桌面上的物体A质量为m1,系一细绳,细绳跨过桌沿的定滑轮后悬挂质量为m2的物体B,先用手使B静止(细绳质量及滑轮摩擦均不计).
(1)求放手后A、B一起运动中绳上的张力FT
(2)若在A上再叠放一个与A质量相等的物体C,绳上张力就增大到,求m1:m2
17.如图所示,一根长为L的轻绳一端固定在O′点,另一端系一质量m的小球,小球可视为质点.将轻绳拉至水平并将小球由位置A静止释放,小球运动到最低点时,轻绳刚好被拉断.O′点下方有一以O为顶点的固定斜面,倾角θ=37°,斜面足够长,且OO′=2L,已知重力加速度为g,忽略空气阻力;求:
(1)轻绳断时的前后瞬间,小球的加速度?
(2)小球落至斜面上的速度大小及方向与水平面夹角的正切值.
18.如图所示,一根轻绳的两端分别固定在两根足够高的竖直杆顶端 A、B 处,A、B 两点水平距离为 16m,高度差为 2m,A、B 间绳子总长为 20m.将质量为 m=5kg 的滑环悬挂在绳上,不计摩擦,重力加速度 g 取 10m/s2.求:
(1)环静止时绳子所受的拉力大小
(2)滑环从A点向B点滑行的过程中,环重力势能变化量的最大值为多大
(3)若将环从A点由静止释放,绳拉直时不考虑环反弹,环能否滑到B点,试说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【详解】
A. 小熊向右匀速运动时,绳中的乙张力等于Mg,,小熊与每个抓脚间的静摩擦力不是最大静摩擦力,故A不符合题意;
B.小环碰到钉子时,小熊在爪子中没有滑动,小熊与每个抓脚间的摩擦力是静摩擦力,绳中的张力不可能大于,故B不符合题意;
C. 小熊到达最高点的速度可能不为0,所以小熊上升的最大高度可能小于为,故B不符合题意;
D. 小环碰到钉子时,对小熊进行受力受力,当小熊与每个抓脚间的静摩擦力是最大静摩擦力时,由向心力公式
解得:
所以,速度不能超过,故D符合题意.
2.D
【解析】
【详解】
3.A
【解析】
【详解】
伽利略的物理思想方法的研究顺序是提出假说,数学推理,实验验证,合理外推,典型的就是牛顿第一定律的最初研究.
4.D
【解析】
【详解】
在伽利略的斜面实验中,小球从一个斜面滚到另一个斜面,斜面弹力是不同的,势能先减小后增大,速度先增大后减小;恒量应是能量,包括动能和势能,故D正确,ABC错误。
故选D。
5.D
【解析】
【分析】
【详解】
A.由动量表达式
动能
可得两者的大小关系为
则动量大的物体,质量关系不清楚,则动能不一定大,A错误;
B.系统的内力总是成对出现其总冲量为零,故系统的动量是否守恒是看外力的总冲量为零,故B错误;
C.一对相互作用力大小相等,方向相反,但两物体的位移不一定相同,则总功可以为零(一对静摩擦力)或不为零(一对滑动摩擦力),故C错误;
D.除重力做功外,其他力不做功,物体只发生动能和势能的相互转化,满足机械能守恒条件,物体的机械能一定守恒,故D正确。
故选D。
6.AB
【解析】
【详解】
A.小球缓慢运动,合力为零,设绳子与竖直方向的夹角为θ,在垂直绳子方向有:
Fcosθ=mgsinθ
解得:
F=mgtanθ
θ逐渐增大,则拉力F逐渐增大,故A正确。
B.拉力F与小球速度的夹角为锐角,所以拉力对小球做正功,故B正确。
C.绳子的拉力方向与速度方向始终垂直,则绳子张力对小球不做功,故C错误。
D.根据功能原理可知,拉力F对小球做正功,小球的机械能增加,故D错误。
故选AB.
7.BD
【解析】
【详解】
A.由图2可知,在弹簧恢复原长过程,物块的位移是0.2m,根据
可知做匀加速直线运动的加速度
故A错误;
B.初始状态物块处于静止状态有
加外力瞬间根据牛顿第二定律有
弹簧弹力不能突变,因此有
F=ma
解得
m=2kg
k=100N/m
在弹簧恢复原长瞬间,有
F1-mg=ma
得弹簧恢复原长瞬间弹力
F1=25N
此时刻物块的速度
v=at=1m/s
所以外力F的功率为
P=Fv=25W
故B正确;
C.在弹簧恢复原长过程中,重力做功
WG=-mgh=-4J
根据重力势能变化量与重力做功的关系
得重力势能增加4J,故C错误。
D.物块和弹簧组成系统的机械能变化量等于外力F做功,在弹簧恢复原长过程中,外力F做功是图2梯形面积,即
故D正确;
故选BD。
8.BC
【解析】
【详解】
A.由图可知,此时飞机向上减速,有向下的加速度,因此处于失重状态,故A错误;
BC.由动能定理
可知,图像的斜率的绝对值表示合外力,因此有
则加速度为
代入数据解得
说明飞机除了受到重力以外还受到空气对它竖直向上的力,空气对飞机做正功,由功能关系可知,飞机的机械能增大,故BC正确;
D.由牛顿第二定律可得
根据动能公式
可得,在图像中,飞机最大速度为
则最大功率为
代入数据解得
故D错误。
故选BC。
9.AD
【解析】
【详解】
AB.由题图乙可知,Ob段小球B受到的弹力随着速度的增大而减小,所以弹力方向向上,当时弹力:
即
当时,此时:
所以
则:
所以,故A正确,B错误;
C.当小球B在最高点速度为零时,小球A转到最高点时速度最小,设最小速度为v,根据机械能守恒定律,减少的重力势能等于增加的动能:
所以最小的速度,故C错误;
D.若小球A到达最高点时不受杆给的弹力,则有,根据系统机械能守恒,小球B转到最高点后速度设为,以圆心所在的平面为重力势能的参考平面有:
解得,在题图乙中有效范围之内,该假设成立,故D正确.
10.AD
【解析】
【分析】
【详解】
A.由低轨道进入高轨道,即由轨道Ⅰ进入轨道Ⅱ需要加速做离心运动,A正确;
B.根据开普勒第三定律,轨道Ⅰ的轨道半径小于轨道Ⅲ的轨道半径,则沿轨道Ⅰ运行的周期小于天和核心舱沿轨道Ⅲ运行的周期,B错误;
C.神舟十二号载人飞船沿轨道Ⅱ运动到对接点过程中,根据开普勒第二定律,速度越来越小 ,C错误;
D.根据开普第三定律
解得
D正确。
故选AD。
11.5.2m
【解析】
【详解】
A物体从斜面下滑过程中由机械能守恒定律得
解得
设下滑过程中所用的时间为t1,由运动学公式得
解得
t1=0.4s
A到水平面上做匀速运动,在0.6s的时间内的位移
xA=vAt2=1.2m
B物体在摩擦力的作用下做匀减速运动,设其加速度为aB
aB=μg=2m/s2
据运动学可知,当B停下来所用的时间为2.5s,所用可知,A与B相遇时B未停,设在t=1s的时间的B物体的位移为
xB=v0t at2
解得
xB=4m
所用Q点到O点的距离
L=xA+xB=1.2m+4m=5.2m
12.
【解析】
【分析】
【详解】
当轻杆由水平位置转至竖直位置的运动过程中,A、B系统机械能守恒,有
A、B球角速度相同,有
,
得
解得
对A球由动能定理得
解得杆对A球所做功
13.(1);(2)
【解析】
【详解】
(1)车在时间t内向左走的位移:
,
又车做匀加速运动,则:
,
所以:
;
(2)t时刻此时汽车的速度
;
由运动的分解知识可知,汽车速度v汽沿绳的分速度与重物m的速度大小相等,即:
,
得:
.
14.(1)2.25m;(2)2.5m。
【解析】
【分析】
【详解】
(1)设物块滑上木板的速度为v0,则有
物块滑上木板,对于木板向右的滑动摩擦力小于地面可以施加的最大静摩力,即
所以木板静止不动。
对物块,根据动能定理有
解得
x=2.25m
(2)对物块,根据牛顿第二定律
对于板,根据牛顿第二定律
设达到共速时的时间为t,则有
共速后一起运动,一起减速运动,则有
物块对地的位移
一起运动时,根据速度位移公式
总位移
代入数据解得
x′=2.5m
15.(1) (2)
【解析】
【详解】
本题考查重力势能的计算及重力做功与重力势能变化间的关系.
(1)开始时,斜面上半条链条的重力势能
开始时,悬在空中半条链条的重力势能
开始时链条的重力势能
右侧滑出斜面时链条的重力势能
(2)此过程中重力势能的变化量
则此过程中重力做的功
点睛:重力对物体所做的功与物体重力势能变化量相反,即.
16.(1);(2)1:2
【解析】
【分析】
(1)放手后两物体一起做匀加速直线运动,分别以AB为研究对象进行受力分析,由牛顿第二定律可求得绳子的拉力;(2)分别对B及AC整体受力分析,由牛顿第二定律可列出绳子张力的表达式,根据题意可得出质量的关系.
【详解】
解:(1)对B,由牛顿第二定律有:
对A,由牛顿第二定律有:
解得:
(2)对B,由牛顿第二定律有:
对AC,由牛顿第二定律有:
解得:
由,得:
所以m1:m2=1:2
【点睛】
对于连接体问题要注意正确受力分析,合理选择研究对象进行分析,列牛顿第二定律进行分析即可解决.
17.(1) ,方向竖直向上;,方向竖直向下
(2) ,与水平面夹角为β,
【解析】
【详解】
(1)小球从A到最低点,由动能定理:
mgL=
得:
v0=
轻绳断前瞬间,小球的加速度
a向==2g,方向竖直向上
轻绳断后瞬间,小球的加速度
a==g,方向竖直向下
(2)以O为坐标原点,OO′为y轴,建立直角坐标系,斜面
对应方程y=x
平抛轨迹
x=v0t
y=L-gt2
消去t得
y=L-
联立解得:
x=L,y= L
平抛的高度
h=
小球落至斜面上的速度:
v=
与水平面夹角为β,
tanβ=
18.(1)41.67N;(2)350J;(3)环能滑到B点.
【解析】
【详解】
(1)环静止时∠BCF=∠ECF=θ,所以
LBCsinθ+LACsinθ=BD
所以
即
θ=53°
2Fcosθ=mg
解得
F=41.67N
(2)AD=2m,则ED=ADtan53°=m,所以FE=m.
FC:AD=EF:ED,得FC=5 m
所以AC高度差为△h=7m,
△EPm=mg△h=350J
(3)若将环从A点由静止释放,绳拉直时不考虑环反弹,不计摩擦力
根据机械能守恒知
mgh=mv2
代入数据解得
v=2m/s
所以环可以滑到B点.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图甲所示的“抓娃娃机”是老少皆宜的一种娱乐工具.若抓小熊的爪子有四个抓脚,某次抓小熊简化为如图乙所示(只画了左、右两个抓脚,前、后两个没画),其中一段过程如下:当小熊(可视为质点)被爪子夹紧,爪子通过轻绳悬挂在小环上,小环套在水平光滑细杆上,小熊质量为,到小环的距离为,小熊与每个抓脚间的最大静摩擦力均为.小环和小熊以速度向右匀速运动,小环碰到杆上的钉子后立刻停止,小熊向上摆动.整个过程中,小熊在爪子中没有滑动.小环和爪子的质量均不计,重力加速度为.下列说法正确的是( )
A.小熊向右匀速运动时,绳中的乙张力等于
B.小环碰到钉子时,绳中的张力大于
C.小熊上升的最大高度为
D.速度不能超过
2.如图所示,卷扬机的绳索通过定滑轮用力F拉位于粗糙斜面上的木箱,使之沿斜面加速向上移动.在移动过程中,下列说法中正确的是( )
A.木箱克服重力所做的功等于木箱机械能的增加
B.F对木箱做的功等于木箱增加的动能与木箱克服摩擦力所做的功之和
C.F对木箱做的功等于木箱克服摩擦力和克服重力所做的功之和
D.F对木箱做的功等于木箱增加的机械能与木箱克服摩擦力做的功之和
3.爱因斯坦说:“伽利略(Galileo galilei,1564﹣1642)的发现以及他所应用的科学推理方法,是人类思想史上最伟大的成就之一,标志着物理学的真正开端.”在科学史上,伽利略享有“近代科学方法论的奠基人”的美誉.根据你对物理学的学习和对伽利略的了解,他的物理思想方法的研究顺序是( )
A.提出假说,数学推理,实验验证,合理外推
B.数学推理,实验验证,合理外推,提出假说
C.实验验证,合理外推,提出假说,数学推理
D.合理外推,提出假说,数学推理,实验验证
4.在伽利略的斜面实验中,小球从一个斜面的某一高度由静止滑下,并运动到另一个斜面的同一高度,小球好像“记得”自己的起始高度,或与高度相关的某个量。“记得”并不是物理学的语言。后来的物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做( )
A.弹力 B.势能 C.速度 D.能量
5.下列说法正确的是( )
A.动量大的物体,它的动能一定也大
B.只要系统内存在摩擦力,系统动量就不可能守恒
C.一对相互作用力所做功的代数和一定为零
D.除重力做功外,其他力不做功,物体的机械能一定守恒
二、多选题
6.如图所示,细线的一端固定于O点,另一端系一小球,在水平拉力F作用下,小球缓慢地在竖直平面内由A点运动到B点的过程中( )
A.拉力F逐渐增大 B.拉力F对小球做正功
C.细绳对小球做负功 D.小球的机械能保持守恒
7.如图(a)所示,竖直放置的轻弹簧下端固定在地面上,上端与质量为m的物块相连(不拴接),初始时处于静止状态。现对物块施加竖直向上的外力F,使物块做匀加速直线运动,经过0.4s弹簧恢复原长,图(b)是外力F随物块位移x变化的图像,重力加速度g取10m/s2,下列说法正确的是( )
A.物块加速度大小为2m/s2
B.弹簧恢复原长的瞬间,拉力的功率为25W
C.在弹簧恢复原长的过程中,物块的重力势能增加了2J
D.在弹簧恢复原长过程中,物块和弹簧组成的系统机械能增加了3J
8.在一次航模比赛中,某同学遥控航模飞机竖直上升,某段过程中其动能Ek随位移x变化的关如图所示。已知飞机质量为1kg,重力加速度g=10m/s2,此过程中飞机( )
A.处于超重状态 B.机械能增大
C.加速度大小为4.5m/s2 D.输出功率最大值为27W
9.如图甲所示,轻杆长为3R,已知,两端分别固定着质量相等的两个小球A和B,杆上O点装有光滑的水平转轴,给小球B一个合适的速度能够让小球A和小球B绕着O在竖直面内做圆周运动,忽略空气阻力.设小球B在最高点的速度为v,小球B受到的弹力大小为F,其图象如图乙所示,则下列说法正确的是( )
A.当地的重力加速度为
B.小球B的质量为
C.由图乙分析可得到小球A转到最高点时的最小速度为
D.若,当小球A转到最高点时受到的弹力有可能为零
10.2021年6月17日,神舟十二号载人飞船与天和核心舱完成对接,航天员聂海胜,刘伯明、汤洪波进入天和核心舱,标志着中国人首次进入了自己的空间站。对接过程如图所示,天和核心舱处于半径为的圆轨道Ⅲ,神舟十二号飞船处于半径为的圆轨道Ⅰ,运行周期为,通过变轨操作后,沿椭圆轨道Ⅱ运动到处与天和核心舱对接。则神舟十二号飞船( )
A.需要加速才能由轨道Ⅰ进入轨道Ⅱ
B.沿轨道Ⅰ运行的周期大于天和核心舱沿轨道Ⅲ运行的周期
C.沿轨道Ⅱ运动到对接点过程中,速度不断增大
D.沿轨道Ⅱ运行的周期为
三、解答题
11.如图所示,倾角θ=30°的斜面上的P点距水平面高h=0.2m,光滑滑块A自P点由静止释放,同时滑块B自水平面上的Q点以速度v0=5m/s向右运动,已知B与水平面间的动摩擦因数μ=0.2,滑块A释放后经过t=1s在水平面上刚好与滑块B相遇。假设滑块A 滑过O点时机械能不损失。g取10m/s2,两滑块均可视为质点。求Q点与斜面底端O点的距离。
12.如图所示,轻杆AB长l,两端各连接一个小球(可视为质点),两小球质量关系为,轻杆绕距B端处的O轴在竖直平面内逆时针自由转动。当轻杆由水平位置转至竖直位置的运动过程中,求杆对A球所做功。
13.一辆车通过一根跨过定滑轮的轻绳子提升一个质量为m的重物,开始车在滑轮的正下方,绳子的端点离滑轮的距离是H.车由静止开始向左做匀加速运动,此时各段绳子刚好伸直,经过时间t绳子与水平方向的夹角为,如图所示,
试求:(1)车向左运动的加速度的大小;
(2)重物在t时刻速度的大小.
14.如图所示,光滑平台AB左端墙壁固定有一个轻弹簧,弹簧右侧有一个质量为2kg的小物块。紧靠平台右端放置一个质量为1kg的木板,上表面与平台等高且足够长。物块与木板上表面、木板与地面的动摩擦因数均为0.2,且最大静摩擦力等于滑动摩擦力。已知弹簧被压缩至O点时弹性势能为9J,重力加速度取10m/s2。试求:
(1)物块最终与平台右端B处的距离是多少;
(2)若木板与地面的动摩擦因数为0.1,其他条件不变,物块最终与平台右端B处的距离是多少。
15.如图所示,有一条长为L的均匀金属链条,一半长度在光滑斜面上,斜面倾角为θ,另一半长度沿竖直方向下垂在空中,当链条从静止开始释放后链条滑动,以斜面最高点为重力势能的零点,则:
(1)开始时和链条刚好从右侧全部滑出斜面时重力势能各是多大?
(2)重力在此过程中做了多少功?
16.如图所示,光滑水平桌面上的物体A质量为m1,系一细绳,细绳跨过桌沿的定滑轮后悬挂质量为m2的物体B,先用手使B静止(细绳质量及滑轮摩擦均不计).
(1)求放手后A、B一起运动中绳上的张力FT
(2)若在A上再叠放一个与A质量相等的物体C,绳上张力就增大到,求m1:m2
17.如图所示,一根长为L的轻绳一端固定在O′点,另一端系一质量m的小球,小球可视为质点.将轻绳拉至水平并将小球由位置A静止释放,小球运动到最低点时,轻绳刚好被拉断.O′点下方有一以O为顶点的固定斜面,倾角θ=37°,斜面足够长,且OO′=2L,已知重力加速度为g,忽略空气阻力;求:
(1)轻绳断时的前后瞬间,小球的加速度?
(2)小球落至斜面上的速度大小及方向与水平面夹角的正切值.
18.如图所示,一根轻绳的两端分别固定在两根足够高的竖直杆顶端 A、B 处,A、B 两点水平距离为 16m,高度差为 2m,A、B 间绳子总长为 20m.将质量为 m=5kg 的滑环悬挂在绳上,不计摩擦,重力加速度 g 取 10m/s2.求:
(1)环静止时绳子所受的拉力大小
(2)滑环从A点向B点滑行的过程中,环重力势能变化量的最大值为多大
(3)若将环从A点由静止释放,绳拉直时不考虑环反弹,环能否滑到B点,试说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【详解】
A. 小熊向右匀速运动时,绳中的乙张力等于Mg,,小熊与每个抓脚间的静摩擦力不是最大静摩擦力,故A不符合题意;
B.小环碰到钉子时,小熊在爪子中没有滑动,小熊与每个抓脚间的摩擦力是静摩擦力,绳中的张力不可能大于,故B不符合题意;
C. 小熊到达最高点的速度可能不为0,所以小熊上升的最大高度可能小于为,故B不符合题意;
D. 小环碰到钉子时,对小熊进行受力受力,当小熊与每个抓脚间的静摩擦力是最大静摩擦力时,由向心力公式
解得:
所以,速度不能超过,故D符合题意.
2.D
【解析】
【详解】
3.A
【解析】
【详解】
伽利略的物理思想方法的研究顺序是提出假说,数学推理,实验验证,合理外推,典型的就是牛顿第一定律的最初研究.
4.D
【解析】
【详解】
在伽利略的斜面实验中,小球从一个斜面滚到另一个斜面,斜面弹力是不同的,势能先减小后增大,速度先增大后减小;恒量应是能量,包括动能和势能,故D正确,ABC错误。
故选D。
5.D
【解析】
【分析】
【详解】
A.由动量表达式
动能
可得两者的大小关系为
则动量大的物体,质量关系不清楚,则动能不一定大,A错误;
B.系统的内力总是成对出现其总冲量为零,故系统的动量是否守恒是看外力的总冲量为零,故B错误;
C.一对相互作用力大小相等,方向相反,但两物体的位移不一定相同,则总功可以为零(一对静摩擦力)或不为零(一对滑动摩擦力),故C错误;
D.除重力做功外,其他力不做功,物体只发生动能和势能的相互转化,满足机械能守恒条件,物体的机械能一定守恒,故D正确。
故选D。
6.AB
【解析】
【详解】
A.小球缓慢运动,合力为零,设绳子与竖直方向的夹角为θ,在垂直绳子方向有:
Fcosθ=mgsinθ
解得:
F=mgtanθ
θ逐渐增大,则拉力F逐渐增大,故A正确。
B.拉力F与小球速度的夹角为锐角,所以拉力对小球做正功,故B正确。
C.绳子的拉力方向与速度方向始终垂直,则绳子张力对小球不做功,故C错误。
D.根据功能原理可知,拉力F对小球做正功,小球的机械能增加,故D错误。
故选AB.
7.BD
【解析】
【详解】
A.由图2可知,在弹簧恢复原长过程,物块的位移是0.2m,根据
可知做匀加速直线运动的加速度
故A错误;
B.初始状态物块处于静止状态有
加外力瞬间根据牛顿第二定律有
弹簧弹力不能突变,因此有
F=ma
解得
m=2kg
k=100N/m
在弹簧恢复原长瞬间,有
F1-mg=ma
得弹簧恢复原长瞬间弹力
F1=25N
此时刻物块的速度
v=at=1m/s
所以外力F的功率为
P=Fv=25W
故B正确;
C.在弹簧恢复原长过程中,重力做功
WG=-mgh=-4J
根据重力势能变化量与重力做功的关系
得重力势能增加4J,故C错误。
D.物块和弹簧组成系统的机械能变化量等于外力F做功,在弹簧恢复原长过程中,外力F做功是图2梯形面积,即
故D正确;
故选BD。
8.BC
【解析】
【详解】
A.由图可知,此时飞机向上减速,有向下的加速度,因此处于失重状态,故A错误;
BC.由动能定理
可知,图像的斜率的绝对值表示合外力,因此有
则加速度为
代入数据解得
说明飞机除了受到重力以外还受到空气对它竖直向上的力,空气对飞机做正功,由功能关系可知,飞机的机械能增大,故BC正确;
D.由牛顿第二定律可得
根据动能公式
可得,在图像中,飞机最大速度为
则最大功率为
代入数据解得
故D错误。
故选BC。
9.AD
【解析】
【详解】
AB.由题图乙可知,Ob段小球B受到的弹力随着速度的增大而减小,所以弹力方向向上,当时弹力:
即
当时,此时:
所以
则:
所以,故A正确,B错误;
C.当小球B在最高点速度为零时,小球A转到最高点时速度最小,设最小速度为v,根据机械能守恒定律,减少的重力势能等于增加的动能:
所以最小的速度,故C错误;
D.若小球A到达最高点时不受杆给的弹力,则有,根据系统机械能守恒,小球B转到最高点后速度设为,以圆心所在的平面为重力势能的参考平面有:
解得,在题图乙中有效范围之内,该假设成立,故D正确.
10.AD
【解析】
【分析】
【详解】
A.由低轨道进入高轨道,即由轨道Ⅰ进入轨道Ⅱ需要加速做离心运动,A正确;
B.根据开普勒第三定律,轨道Ⅰ的轨道半径小于轨道Ⅲ的轨道半径,则沿轨道Ⅰ运行的周期小于天和核心舱沿轨道Ⅲ运行的周期,B错误;
C.神舟十二号载人飞船沿轨道Ⅱ运动到对接点过程中,根据开普勒第二定律,速度越来越小 ,C错误;
D.根据开普第三定律
解得
D正确。
故选AD。
11.5.2m
【解析】
【详解】
A物体从斜面下滑过程中由机械能守恒定律得
解得
设下滑过程中所用的时间为t1,由运动学公式得
解得
t1=0.4s
A到水平面上做匀速运动,在0.6s的时间内的位移
xA=vAt2=1.2m
B物体在摩擦力的作用下做匀减速运动,设其加速度为aB
aB=μg=2m/s2
据运动学可知,当B停下来所用的时间为2.5s,所用可知,A与B相遇时B未停,设在t=1s的时间的B物体的位移为
xB=v0t at2
解得
xB=4m
所用Q点到O点的距离
L=xA+xB=1.2m+4m=5.2m
12.
【解析】
【分析】
【详解】
当轻杆由水平位置转至竖直位置的运动过程中,A、B系统机械能守恒,有
A、B球角速度相同,有
,
得
解得
对A球由动能定理得
解得杆对A球所做功
13.(1);(2)
【解析】
【详解】
(1)车在时间t内向左走的位移:
,
又车做匀加速运动,则:
,
所以:
;
(2)t时刻此时汽车的速度
;
由运动的分解知识可知,汽车速度v汽沿绳的分速度与重物m的速度大小相等,即:
,
得:
.
14.(1)2.25m;(2)2.5m。
【解析】
【分析】
【详解】
(1)设物块滑上木板的速度为v0,则有
物块滑上木板,对于木板向右的滑动摩擦力小于地面可以施加的最大静摩力,即
所以木板静止不动。
对物块,根据动能定理有
解得
x=2.25m
(2)对物块,根据牛顿第二定律
对于板,根据牛顿第二定律
设达到共速时的时间为t,则有
共速后一起运动,一起减速运动,则有
物块对地的位移
一起运动时,根据速度位移公式
总位移
代入数据解得
x′=2.5m
15.(1) (2)
【解析】
【详解】
本题考查重力势能的计算及重力做功与重力势能变化间的关系.
(1)开始时,斜面上半条链条的重力势能
开始时,悬在空中半条链条的重力势能
开始时链条的重力势能
右侧滑出斜面时链条的重力势能
(2)此过程中重力势能的变化量
则此过程中重力做的功
点睛:重力对物体所做的功与物体重力势能变化量相反,即.
16.(1);(2)1:2
【解析】
【分析】
(1)放手后两物体一起做匀加速直线运动,分别以AB为研究对象进行受力分析,由牛顿第二定律可求得绳子的拉力;(2)分别对B及AC整体受力分析,由牛顿第二定律可列出绳子张力的表达式,根据题意可得出质量的关系.
【详解】
解:(1)对B,由牛顿第二定律有:
对A,由牛顿第二定律有:
解得:
(2)对B,由牛顿第二定律有:
对AC,由牛顿第二定律有:
解得:
由,得:
所以m1:m2=1:2
【点睛】
对于连接体问题要注意正确受力分析,合理选择研究对象进行分析,列牛顿第二定律进行分析即可解决.
17.(1) ,方向竖直向上;,方向竖直向下
(2) ,与水平面夹角为β,
【解析】
【详解】
(1)小球从A到最低点,由动能定理:
mgL=
得:
v0=
轻绳断前瞬间,小球的加速度
a向==2g,方向竖直向上
轻绳断后瞬间,小球的加速度
a==g,方向竖直向下
(2)以O为坐标原点,OO′为y轴,建立直角坐标系,斜面
对应方程y=x
平抛轨迹
x=v0t
y=L-gt2
消去t得
y=L-
联立解得:
x=L,y= L
平抛的高度
h=
小球落至斜面上的速度:
v=
与水平面夹角为β,
tanβ=
18.(1)41.67N;(2)350J;(3)环能滑到B点.
【解析】
【详解】
(1)环静止时∠BCF=∠ECF=θ,所以
LBCsinθ+LACsinθ=BD
所以
即
θ=53°
2Fcosθ=mg
解得
F=41.67N
(2)AD=2m,则ED=ADtan53°=m,所以FE=m.
FC:AD=EF:ED,得FC=5 m
所以AC高度差为△h=7m,
△EPm=mg△h=350J
(3)若将环从A点由静止释放,绳拉直时不考虑环反弹,不计摩擦力
根据机械能守恒知
mgh=mv2
代入数据解得
v=2m/s
所以环可以滑到B点.
答案第1页,共2页
答案第1页,共2页
