高中数学苏教版(2022春 )选择性必修第二册 章末复习课(课件 共64张PPT)
文档属性
| 名称 | 高中数学苏教版(2022春 )选择性必修第二册 章末复习课(课件 共64张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 13:32:21 | ||
图片预览






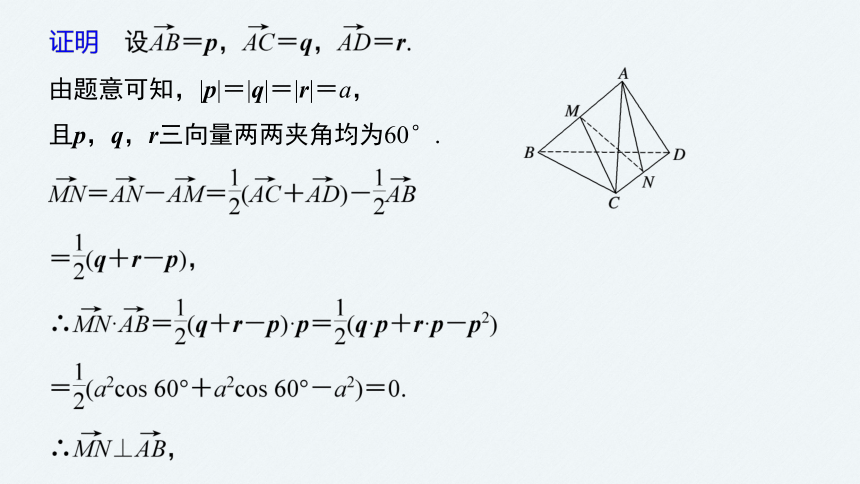
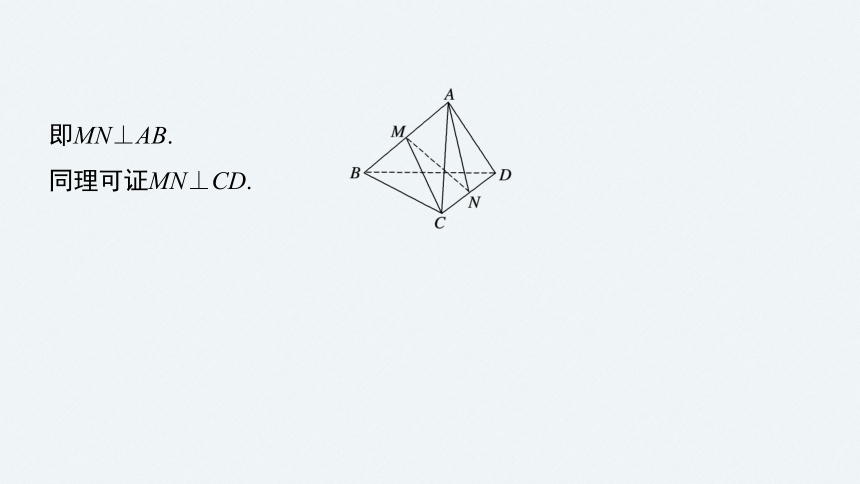

文档简介
(共64张PPT)
章末复习课
第6章 空间向量与立体几何
一、空间向量的线性运算与数量积
二、利用空间向量证明位置关系
三、利用空间向量求空间角
内容索引
知识网络
随堂演练
四、利用空间向量计算距离
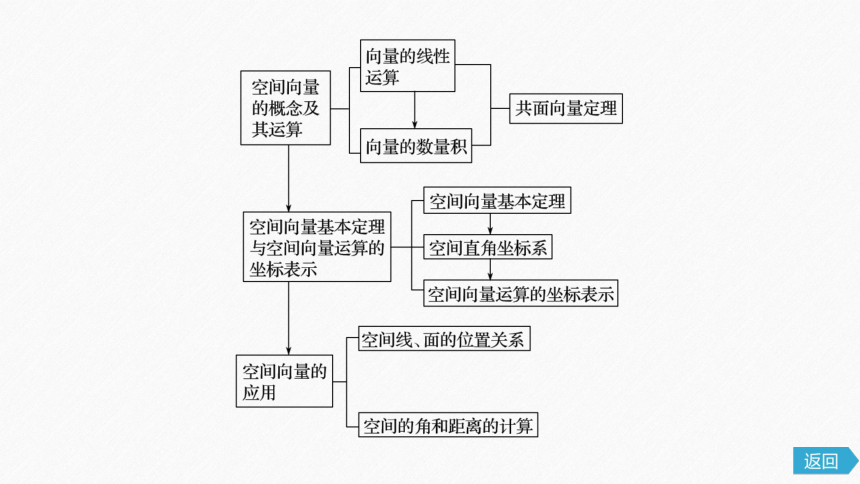
知识网络
一、空间向量的线性运算与数量积
1.向量的线性运算的关键是熟练掌握向量加减运算的平行四边形法则、三角形法则及各运算公式,理解向量运算法则、运算律及其几何意义.
2.利用数量积可以解决有关垂直、夹角、长度问题,解决问题的两条途径:一是根据数量积的定义;二是利用坐标运算.
(1)a≠0,b≠0,a⊥b a·b=0;
3.空间的运算,应注重提高逻辑推理、数学运算核心素养.
1
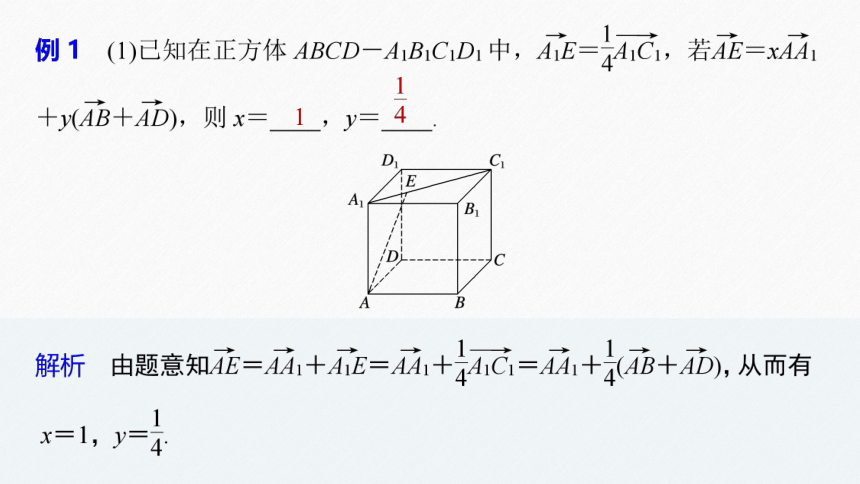
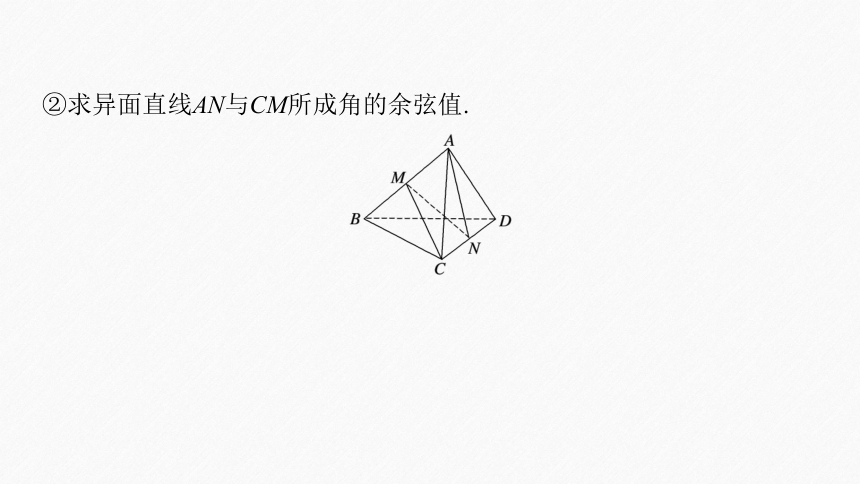
(2)如图所示,已知空间四边形ABCD的各边和对角线的长都等于a,点M,N分别是AB,CD的中点.
①求证:MN⊥AB,MN⊥CD;
由题意可知,|p|=|q|=|r|=a,
且p,q,r三向量两两夹角均为60°.
即MN⊥AB.
同理可证MN⊥CD.
②求异面直线AN与CM所成角的余弦值.
反思感悟 空间向量的数乘运算及向量共面的充要条件
(1)空间向量的数乘运算、共线向量的概念、向量共线的充要条件与平面向量的性质是一致的.
A.(3,0,0) B.(0,3,0)
C.(0,0,3) D.(0,0,-3)
√
(2) 如图所示,在平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长度都为1,且两两夹角为60°.
〈a,b〉=〈b,c〉=〈c,a〉=60°,
=a2+b2+c2+2(a·b+b·c+c·a)
=b2-a2+a·c+b·c=1,
二、利用空间向量证明位置关系
1.用空间向量判断空间中位置关系的类型有线线平行、线线垂直、线面平行、线面垂直、面面平行、面面垂直;判断证明的基本思想是转化为线线关系或者利用平面的法向量、利用向量的共线和垂直进行证明.
2.将立体几何的线面关系转化为向量间的关系,可以培养学生的逻辑思维能力和数学运算能力.
例2 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
(1)求证:BM∥平面ADEF;
证明 ∵平面ADEF⊥平面ABCD,
平面ADEF∩平面ABCD=AD,
AD⊥ED,ED 平面ADEF,
∴ED⊥平面ABCD.
则D(0,0,0),A(2,0,0),
B(2,2,0),C(0,4,0),E(0,0,2),F(2,0,2).
∵M为EC的中点,
∴M(0,2,1),
又BM 平面ADEF,
∴BM∥平面ADEF.
(2)求证:BC⊥平面BDE.
又DE∩DB=D,∴BC⊥平面BDE.
延伸探究 本例条件不变,如何证明平面BCE⊥平面BDE.
证明 由本例(2)知BC⊥平面BDE,又BC 平面BCE,∴平面BCE⊥平面BDE.
反思感悟 利用空间向量证明或求解立体几何问题时,首先要转化为其坐标运算,再借助于坐标的有关性质求解(证).
跟踪训练2 如图,在正三棱锥P-ABC中,三条侧棱两两互相垂直,G是△PAB的重心,E,F分别为BC,PB上的点,且BE∶EC=PF∶FB=1∶2.求证:平面GEF⊥平面PBC.
证明 方法一 如图,以三棱锥的顶点P为原点,以PA,PB,PC所在直线分别作为x轴、y轴、z轴建立空间直角坐标系.
令PA=PB=PC=3,则A(3,0,0),F(0,1,0),G(1,1,0),P(0,0,0),
又PA⊥平面PBC,∴FG⊥平面PBC.
又FG 平面EFG,∴平面EFG⊥平面PBC.
方法二 同方法一,建立空间直角坐标系,
则E(0,2,1),F(0,1,0),G(1,1,0).
设平面EFG的法向量是n=(x,y,z),
即n=(0,1,-1).
即平面PBC的法向量与平面EFG的法向量互相垂直,
所以平面EFG⊥平面PBC.
三、利用空间向量求空间角
1.空间向量与空间角的关系
(1)设异面直线l1,l2的方向向量分别为m1,m2,则l1与l2的夹角θ满足cos θ=|cos〈m1,m2〉|.
(2)设直线l的方向向量和平面α的法向量分别为m,n,则直线l与平面α的夹角θ满足sin θ=|cos〈m,n〉|.
(3)设n1,n2分别是两个平面α,β的法向量,则二面角的平面角与这两个平面的法向量的夹角相等或互补.
2.通过利用向量计算空间的角,可以培养学生的逻辑思维能力和数学运算能力.
例3 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1= ,点E,F分别是平面A1B1C1D1,平面BCC1B1的中心.以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.试用向量方法解决下列问题:
(1)求异面直线AF和BE所成的角;
∴直线AF和BE所成的角为90°.
(2)求直线AF和平面BEC所成角的正弦值.
反思感悟 (1)在建立空间直角坐标系的过程中,一定要依据题目所给几何图形的特征,建立合理的空间直角坐标系,这样才会容易求得解题时需要的坐标.
(2)求直线和平面所成的角、二面角类问题有两种思路:转化为两条直线所成的角、利用平面的法向量.
跟踪训练3 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
则C(0,0,0),A(1,1,0),B(1,-1,0).
所以m为平面PAC的一个法向量.
取x=a,
可得n=(a,-a,-2),依题意得,
则a=1(负值舍去).
设直线PA与平面EAC所成的角为θ,
四、利用空间向量计算距离
1.空间距离的计算
2.通过利用向量计算空间距离,可以培养学生的逻辑思维能力和数学运算能力.
例4 在三棱锥B-ACD中,平面ABD⊥平面ACD,若棱长AC=CD=AD=AB=1,且∠BAD=30°,求点D到平面ABC的距离.
解 如图所示,以AD的中点O为原点,以OD,OC所在直线为x轴、y轴,过O作OM⊥平面ACD交AB于M,以直线OM为z轴建立空间直角坐标系,
设n=(x,y,z)为平面ABC的一个法向量,
反思感悟 利用向量法求点面距,只需求出平面的一个法向量和该点与平面内任一点连线表示的向量,代入公式求解即可.
跟踪训练4 (1)在长方体ABCD-A1B1C1D1中,AB=BC=a,AA1=2a,则点D1到直线AC的距离为
√
解析 方法一 连接BD,AC交于点O(图略),
方法二 如图建立空间直角坐标系,易得C(a,a,0),D1(0,a,2a),
则点D1到直线AC的距离为
(2)在三棱锥P-ABC中,PC⊥底面ABC,∠BAC=90°,AB=AC=4,∠PBC=45°,则点C到平面PAB的距离是
√
解析 方法一 建立如图所示的空间直角坐标系,
则A(0,0,0),B(4,0,0),
设平面PAB的法向量为m=(x,y,z),
方法二 ∵PC⊥底面ABC,
∴PC⊥AB,又AB⊥AC,
且PC∩AC=C,PC,AC 平面PAC,
∴AB⊥平面PAC,∴AB⊥PA,
∵AC=AB=4,
令点C到平面PAB的距离为d,
∵VP-ABC=VC-PAB,
1.知识清单:
(1)空间向量的概念及运算.
(2)利用空间向量证明位置关系.
(3)利用空间向量求空间角.
(4)利用空间向量求距离.
2.方法归纳:坐标法、转化化归.
3.常见误区:
(1)数量积运算时注意向量的夹角.
(2)注意直线所成的角与向量夹角的区别与联系.
课堂小结
随堂演练
1.已知向量a=(2,-1,3),b=(-4,2,x),则使a⊥b成立的x与使a∥b成立的x分别为
1
2
3
4
√
1
2
3
4
2.已知向量n=(2,0,1)为平面α的法向量,点A(-1,2,1)在α内,则点P(1,2,2)到平面α的距离为
√
1
2
3
4
√
1
2
3
4
解析 因为点D在平面Oyz内,
所以点D的横坐标为0,
又BC=4,原点O是BC的中点,∠BDC=90°,∠DCB=30°,
纵坐标y=-(2-4·sin 30°·cos 60°)=-1,
1
2
3
4
4.已知点E,F分别在正方体ABCD-A1B1C1D1的棱BB1,CC1上,且B1E=2EB,CF=2FC1,则平面AEF与平面ABC所成的二面角的正切值等
于_____.
解析 如图,建立空间直角坐标系.
设正方体的棱长为1,
平面ABC的法向量为n1=(0,0,1),
设平面AEF的法向量为n2=(x,y,z).
1
2
3
4
取x=1,则y=-1,z=3.
故n2=(1,-1,3).
1
2
3
4
本课结束
章末复习课
第6章 空间向量与立体几何
一、空间向量的线性运算与数量积
二、利用空间向量证明位置关系
三、利用空间向量求空间角
内容索引
知识网络
随堂演练
四、利用空间向量计算距离
知识网络
一、空间向量的线性运算与数量积
1.向量的线性运算的关键是熟练掌握向量加减运算的平行四边形法则、三角形法则及各运算公式,理解向量运算法则、运算律及其几何意义.
2.利用数量积可以解决有关垂直、夹角、长度问题,解决问题的两条途径:一是根据数量积的定义;二是利用坐标运算.
(1)a≠0,b≠0,a⊥b a·b=0;
3.空间的运算,应注重提高逻辑推理、数学运算核心素养.
1
(2)如图所示,已知空间四边形ABCD的各边和对角线的长都等于a,点M,N分别是AB,CD的中点.
①求证:MN⊥AB,MN⊥CD;
由题意可知,|p|=|q|=|r|=a,
且p,q,r三向量两两夹角均为60°.
即MN⊥AB.
同理可证MN⊥CD.
②求异面直线AN与CM所成角的余弦值.
反思感悟 空间向量的数乘运算及向量共面的充要条件
(1)空间向量的数乘运算、共线向量的概念、向量共线的充要条件与平面向量的性质是一致的.
A.(3,0,0) B.(0,3,0)
C.(0,0,3) D.(0,0,-3)
√
(2) 如图所示,在平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长度都为1,且两两夹角为60°.
〈a,b〉=〈b,c〉=〈c,a〉=60°,
=a2+b2+c2+2(a·b+b·c+c·a)
=b2-a2+a·c+b·c=1,
二、利用空间向量证明位置关系
1.用空间向量判断空间中位置关系的类型有线线平行、线线垂直、线面平行、线面垂直、面面平行、面面垂直;判断证明的基本思想是转化为线线关系或者利用平面的法向量、利用向量的共线和垂直进行证明.
2.将立体几何的线面关系转化为向量间的关系,可以培养学生的逻辑思维能力和数学运算能力.
例2 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
(1)求证:BM∥平面ADEF;
证明 ∵平面ADEF⊥平面ABCD,
平面ADEF∩平面ABCD=AD,
AD⊥ED,ED 平面ADEF,
∴ED⊥平面ABCD.
则D(0,0,0),A(2,0,0),
B(2,2,0),C(0,4,0),E(0,0,2),F(2,0,2).
∵M为EC的中点,
∴M(0,2,1),
又BM 平面ADEF,
∴BM∥平面ADEF.
(2)求证:BC⊥平面BDE.
又DE∩DB=D,∴BC⊥平面BDE.
延伸探究 本例条件不变,如何证明平面BCE⊥平面BDE.
证明 由本例(2)知BC⊥平面BDE,又BC 平面BCE,∴平面BCE⊥平面BDE.
反思感悟 利用空间向量证明或求解立体几何问题时,首先要转化为其坐标运算,再借助于坐标的有关性质求解(证).
跟踪训练2 如图,在正三棱锥P-ABC中,三条侧棱两两互相垂直,G是△PAB的重心,E,F分别为BC,PB上的点,且BE∶EC=PF∶FB=1∶2.求证:平面GEF⊥平面PBC.
证明 方法一 如图,以三棱锥的顶点P为原点,以PA,PB,PC所在直线分别作为x轴、y轴、z轴建立空间直角坐标系.
令PA=PB=PC=3,则A(3,0,0),F(0,1,0),G(1,1,0),P(0,0,0),
又PA⊥平面PBC,∴FG⊥平面PBC.
又FG 平面EFG,∴平面EFG⊥平面PBC.
方法二 同方法一,建立空间直角坐标系,
则E(0,2,1),F(0,1,0),G(1,1,0).
设平面EFG的法向量是n=(x,y,z),
即n=(0,1,-1).
即平面PBC的法向量与平面EFG的法向量互相垂直,
所以平面EFG⊥平面PBC.
三、利用空间向量求空间角
1.空间向量与空间角的关系
(1)设异面直线l1,l2的方向向量分别为m1,m2,则l1与l2的夹角θ满足cos θ=|cos〈m1,m2〉|.
(2)设直线l的方向向量和平面α的法向量分别为m,n,则直线l与平面α的夹角θ满足sin θ=|cos〈m,n〉|.
(3)设n1,n2分别是两个平面α,β的法向量,则二面角的平面角与这两个平面的法向量的夹角相等或互补.
2.通过利用向量计算空间的角,可以培养学生的逻辑思维能力和数学运算能力.
例3 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1= ,点E,F分别是平面A1B1C1D1,平面BCC1B1的中心.以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.试用向量方法解决下列问题:
(1)求异面直线AF和BE所成的角;
∴直线AF和BE所成的角为90°.
(2)求直线AF和平面BEC所成角的正弦值.
反思感悟 (1)在建立空间直角坐标系的过程中,一定要依据题目所给几何图形的特征,建立合理的空间直角坐标系,这样才会容易求得解题时需要的坐标.
(2)求直线和平面所成的角、二面角类问题有两种思路:转化为两条直线所成的角、利用平面的法向量.
跟踪训练3 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
则C(0,0,0),A(1,1,0),B(1,-1,0).
所以m为平面PAC的一个法向量.
取x=a,
可得n=(a,-a,-2),依题意得,
则a=1(负值舍去).
设直线PA与平面EAC所成的角为θ,
四、利用空间向量计算距离
1.空间距离的计算
2.通过利用向量计算空间距离,可以培养学生的逻辑思维能力和数学运算能力.
例4 在三棱锥B-ACD中,平面ABD⊥平面ACD,若棱长AC=CD=AD=AB=1,且∠BAD=30°,求点D到平面ABC的距离.
解 如图所示,以AD的中点O为原点,以OD,OC所在直线为x轴、y轴,过O作OM⊥平面ACD交AB于M,以直线OM为z轴建立空间直角坐标系,
设n=(x,y,z)为平面ABC的一个法向量,
反思感悟 利用向量法求点面距,只需求出平面的一个法向量和该点与平面内任一点连线表示的向量,代入公式求解即可.
跟踪训练4 (1)在长方体ABCD-A1B1C1D1中,AB=BC=a,AA1=2a,则点D1到直线AC的距离为
√
解析 方法一 连接BD,AC交于点O(图略),
方法二 如图建立空间直角坐标系,易得C(a,a,0),D1(0,a,2a),
则点D1到直线AC的距离为
(2)在三棱锥P-ABC中,PC⊥底面ABC,∠BAC=90°,AB=AC=4,∠PBC=45°,则点C到平面PAB的距离是
√
解析 方法一 建立如图所示的空间直角坐标系,
则A(0,0,0),B(4,0,0),
设平面PAB的法向量为m=(x,y,z),
方法二 ∵PC⊥底面ABC,
∴PC⊥AB,又AB⊥AC,
且PC∩AC=C,PC,AC 平面PAC,
∴AB⊥平面PAC,∴AB⊥PA,
∵AC=AB=4,
令点C到平面PAB的距离为d,
∵VP-ABC=VC-PAB,
1.知识清单:
(1)空间向量的概念及运算.
(2)利用空间向量证明位置关系.
(3)利用空间向量求空间角.
(4)利用空间向量求距离.
2.方法归纳:坐标法、转化化归.
3.常见误区:
(1)数量积运算时注意向量的夹角.
(2)注意直线所成的角与向量夹角的区别与联系.
课堂小结
随堂演练
1.已知向量a=(2,-1,3),b=(-4,2,x),则使a⊥b成立的x与使a∥b成立的x分别为
1
2
3
4
√
1
2
3
4
2.已知向量n=(2,0,1)为平面α的法向量,点A(-1,2,1)在α内,则点P(1,2,2)到平面α的距离为
√
1
2
3
4
√
1
2
3
4
解析 因为点D在平面Oyz内,
所以点D的横坐标为0,
又BC=4,原点O是BC的中点,∠BDC=90°,∠DCB=30°,
纵坐标y=-(2-4·sin 30°·cos 60°)=-1,
1
2
3
4
4.已知点E,F分别在正方体ABCD-A1B1C1D1的棱BB1,CC1上,且B1E=2EB,CF=2FC1,则平面AEF与平面ABC所成的二面角的正切值等
于_____.
解析 如图,建立空间直角坐标系.
设正方体的棱长为1,
平面ABC的法向量为n1=(0,0,1),
设平面AEF的法向量为n2=(x,y,z).
1
2
3
4
取x=1,则y=-1,z=3.
故n2=(1,-1,3).
1
2
3
4
本课结束
