高中数学苏教版(2022春 )选择性必修第二册 §7.3 第2课时 组合数的性质及应用(62张PPT)
文档属性
| 名称 | 高中数学苏教版(2022春 )选择性必修第二册 §7.3 第2课时 组合数的性质及应用(62张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 15:49:26 | ||
图片预览







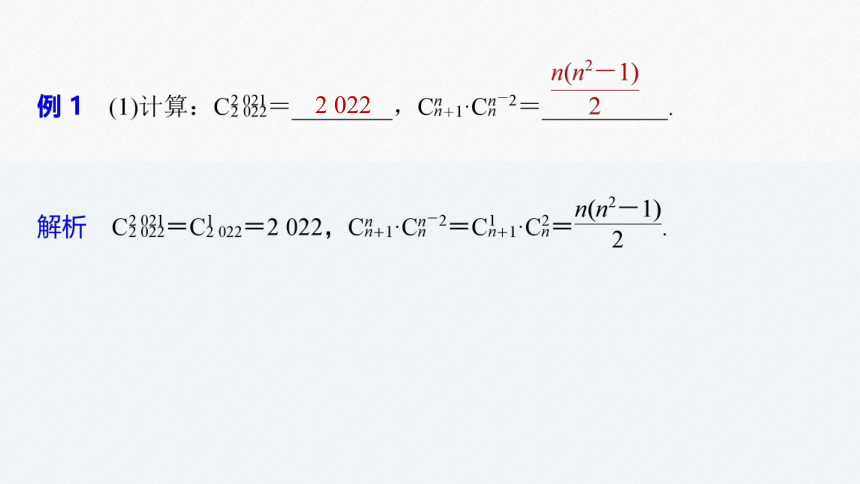



文档简介
(共62张PPT)
第2课时 组合数的性质及应用
第7章 §7.3 组合
1.掌握组合数公式和组合数的性质.
2.能运用组合数的性质进行计算.
3.会用组合数公式解决一些简单的组合问题.
学习目标
对一次学校运动会中的两个特定项目:趣味投羽毛球、3 000米长跑,某班级50位同学必须参加其中一个项目且仅参加一个项目(每一位同学可以在两个项目中任选一个,要求17人参加3 000米跑,其余人参加投羽毛球项目),假设你是班级体育委员,你能算出所有可能的报名情况吗?
导语
随堂演练
课时对点练
一、组合数的性质1
二、组合数的性质2
三、有限制条件的组合问题
内容索引
一、组合数的性质1
问题1 假如我们年级将在月底进行一场篮球比赛.包括体育委员在内,班上篮球运动员有8人,按照篮球比赛规则,比赛时一个球队的上场队员是5人.我们可以形成多少种队员上场方案?我们又可以形成多少种队员不上场方案?这两种方案有什么关系?
知识梳理
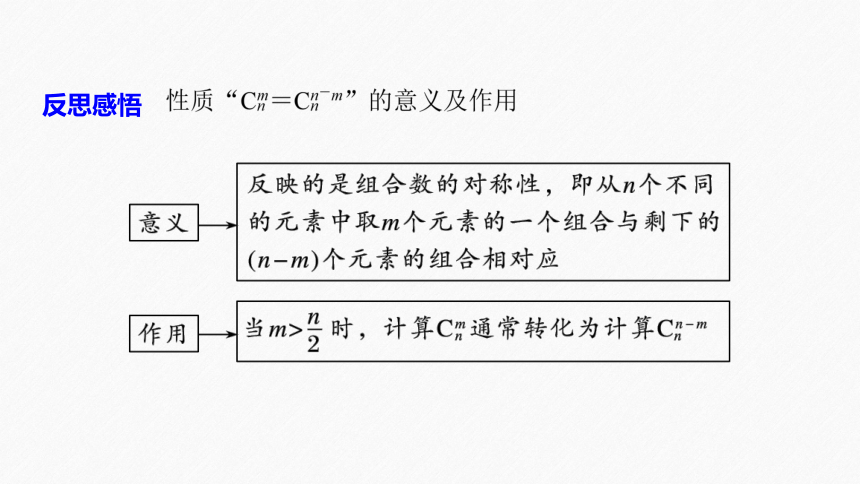
注意点:
(1)体现了“取法”与“剩法”是一一对应的思想.
(2)两边下标相同,上标之和等于下标.
2 022
A.4 B.5 C.6 D.7
√
√
解析 由题意得,2n-3=n+2或2n-3+n+2=20,即n=5或n=7.
反思感悟
A.1 B.10 C.11 D.55
√
得3n+6=4n-2或3n+6+4n-2=18,
解得n=2或n=8(舍去),
28
二、组合数的性质2
知识梳理
注意点:
(1)下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与大的相同的一个组合数.
(2)体现了“含”与“不含”的分类思想.
A.1 B.m C.m+1 D.0
√
√
…
A.12 B.13 C.14 D.15
√
√
三、有限制条件的组合问题
例3 男运动员6名,女运动员4名,其中男女队长各1名,选派5人外出比赛,在下列情形中各有多少种选派方法?
(1)男运动员3名,女运动员2名;
(2)至少有1名女运动员;
解 方法一 (直接法)“至少有1名女运动员”包括以下几种情况,1女4男,2女3男,3女2男,4女1男.
(3)既要有队长,又要有女运动员.
反思感悟 常见的有限制条件的组合问题及解题方法
(1)特殊元素:若要选取的元素中有特殊元素,则要以有无特殊元素,特殊元素的多少作为分类依据.
(2)含有“至多”“至少”等限制语句:要分清限制语句中所包含的情况,可以以此作为分类依据,或采用间接法求解.
(3)分类讨论思想:解题的过程中要善于利用分类讨论思想,将复杂问题分类表达,逐类求解.
跟踪训练3 在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法?
(1)任意选5人;
(2)甲、乙、丙三人必须参加;
(3)甲、乙、丙三人不能参加;
(4)甲、乙、丙三人只能有1人参加.
1.知识清单:
(1)组合数的两个性质及性质的理解.
(2)组合数在实际问题中的应用.
2.方法归纳:分类讨论、间接法.
3.常见误区:不注意组合数中m与n的限制条件;计算时不能构造组合数性质.
课堂小结
随堂演练
1
2
3
4
√
1
2
3
4
2.某研究性学习小组有4名男生和4名女生,一次问卷调查活动需要挑选3名同学参加,其中至少一名女生,则不同的选法种数为
A.120种 B.84种 C.52种 D.48种
√
1
2
3
4
1
2
3
4
4.甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案的种数为______.
96
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
A.4 B.14
C.4或6 D.14或2
16
√
解得x=4或x=6.
2.从5名志愿者中选派4人在星期六和星期日参加公益活动,每人一天,每天两人,则不同的选派方法共有
A.60种 B.48种 C.30种 D.10种
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.已知直线a,直线b,且a∥b,a上有5个点,b上有4个点,则以这九个点为顶点的三角形个数为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.在平面直角坐标系xOy上,平行直线x=n(n=0,1,2,…,5)与平行直线y=n(n=0,1,2,…,5)组成的图形中,矩形共有
A.25个 B.36个 C.100个 D.225个
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)下列等式正确的是
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 A是组合数公式;
两者不相等,故D错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
126
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.男女学生共有8人,从男生中选取2人,从女生中选取1人,共有30种不同的选法,其中女生有______人.
2或3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.高二(1)班共有35名同学,其中男生20名,女生15名,今从中选出3名同学参加活动.
(1)其中某一女生必须在内,不同的选法有多少种?
解 从余下的34名学生中选取2名,
∴不同的选法有561种.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)其中某一女生不能在内,不同的选法有多少种?
∴不同的选法有5 984种.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)恰有2名女生在内,不同的选法有多少种?
∴不同的选法有2 100种.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(4)至少有2名女生在内,不同的选法有多少种?
∴不同的选法有2 555种.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(5)至多有2名女生在内,不同的选法有多少种?
∴不同的选法有6 090种.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.现有8名青年,其中有5名能胜任英语翻译工作,有4名能胜任德语翻译工作(其中有1名青年两项工作都能胜任).现在要从中挑选5名青年承担一项任务,其中3名从事英语翻译工作,2名从事德语翻译工作,则有多少种不同的选法?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 可以分三类:
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.从10名大学毕业生中选3人担任村长助理,则甲、乙至少有1人入选,而丙没有入选的不同选法的种数为
A.28 B.49 C.56 D.85
√
解析 依题意得,满足条件的不同选法的种数为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.某餐厅供应饭菜,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种.现在餐厅准备了5种不同的荤菜,若要保证每位顾客有200种以上不同的选择,则餐厅至少还需准备不同的素菜品种____种(结果用数值表示).
7
解析 设餐厅还需准备x种不同的素菜.
即x(x-1)≥40.
又x≥2,x∈N*,所以x的最小值为7.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.在同一个平面内有一组平行线共8条,另一组平行线共10条,这两组平行线相互不平行,它们共能构成______个平行四边形,共有____个交点.
1 260
80
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.将标号为1,2,…,10的10个球放入标号为1,2,…,10的10个盒子里,每个盒内放一个球,恰好3个球的标号与其在盒子的标号不一致的放入方法种数为
A.120 B.240 C.360 D.720
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.某次足球赛,共32支球队参加,它们先分成8个小组进行循环赛,决出16强(每队均与本组其他队赛一场,各组一、二名晋级16强),这16支球队按确定的程序进行淘汰赛,最后决出冠、亚军,此外还要决出第三名、第四名,问这届世界杯总共进行了多少场比赛?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 可分为如下几类比赛:(1)小组循环赛:每组有 =6(场),8个小组共有48场;
(2)八分之一淘汰赛:8个小组的第一、二名组成16强,根据赛制规则,每两个队比赛一场,可以决出8强,共有8场;
(3)四分之一淘汰赛:根据赛制规则,8强中每两个队比赛一次,可以决出4强,共有4场;
(4)半决赛:根据赛制规则,4强每两个队比赛一场,可以决出参加决赛的两支球队,共有2场;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(5)决赛:两支球队比赛1场确定冠、亚军,4强中的另两支球队比赛1场决出第三、四名,共有2场.
综上,由分类计数原理知,共有48+8+4+2+2=64(场)比赛.
本课结束
第2课时 组合数的性质及应用
第7章 §7.3 组合
1.掌握组合数公式和组合数的性质.
2.能运用组合数的性质进行计算.
3.会用组合数公式解决一些简单的组合问题.
学习目标
对一次学校运动会中的两个特定项目:趣味投羽毛球、3 000米长跑,某班级50位同学必须参加其中一个项目且仅参加一个项目(每一位同学可以在两个项目中任选一个,要求17人参加3 000米跑,其余人参加投羽毛球项目),假设你是班级体育委员,你能算出所有可能的报名情况吗?
导语
随堂演练
课时对点练
一、组合数的性质1
二、组合数的性质2
三、有限制条件的组合问题
内容索引
一、组合数的性质1
问题1 假如我们年级将在月底进行一场篮球比赛.包括体育委员在内,班上篮球运动员有8人,按照篮球比赛规则,比赛时一个球队的上场队员是5人.我们可以形成多少种队员上场方案?我们又可以形成多少种队员不上场方案?这两种方案有什么关系?
知识梳理
注意点:
(1)体现了“取法”与“剩法”是一一对应的思想.
(2)两边下标相同,上标之和等于下标.
2 022
A.4 B.5 C.6 D.7
√
√
解析 由题意得,2n-3=n+2或2n-3+n+2=20,即n=5或n=7.
反思感悟
A.1 B.10 C.11 D.55
√
得3n+6=4n-2或3n+6+4n-2=18,
解得n=2或n=8(舍去),
28
二、组合数的性质2
知识梳理
注意点:
(1)下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与大的相同的一个组合数.
(2)体现了“含”与“不含”的分类思想.
A.1 B.m C.m+1 D.0
√
√
…
A.12 B.13 C.14 D.15
√
√
三、有限制条件的组合问题
例3 男运动员6名,女运动员4名,其中男女队长各1名,选派5人外出比赛,在下列情形中各有多少种选派方法?
(1)男运动员3名,女运动员2名;
(2)至少有1名女运动员;
解 方法一 (直接法)“至少有1名女运动员”包括以下几种情况,1女4男,2女3男,3女2男,4女1男.
(3)既要有队长,又要有女运动员.
反思感悟 常见的有限制条件的组合问题及解题方法
(1)特殊元素:若要选取的元素中有特殊元素,则要以有无特殊元素,特殊元素的多少作为分类依据.
(2)含有“至多”“至少”等限制语句:要分清限制语句中所包含的情况,可以以此作为分类依据,或采用间接法求解.
(3)分类讨论思想:解题的过程中要善于利用分类讨论思想,将复杂问题分类表达,逐类求解.
跟踪训练3 在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人参加市级培训.在下列条件下,有多少种不同的选法?
(1)任意选5人;
(2)甲、乙、丙三人必须参加;
(3)甲、乙、丙三人不能参加;
(4)甲、乙、丙三人只能有1人参加.
1.知识清单:
(1)组合数的两个性质及性质的理解.
(2)组合数在实际问题中的应用.
2.方法归纳:分类讨论、间接法.
3.常见误区:不注意组合数中m与n的限制条件;计算时不能构造组合数性质.
课堂小结
随堂演练
1
2
3
4
√
1
2
3
4
2.某研究性学习小组有4名男生和4名女生,一次问卷调查活动需要挑选3名同学参加,其中至少一名女生,则不同的选法种数为
A.120种 B.84种 C.52种 D.48种
√
1
2
3
4
1
2
3
4
4.甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案的种数为______.
96
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
A.4 B.14
C.4或6 D.14或2
16
√
解得x=4或x=6.
2.从5名志愿者中选派4人在星期六和星期日参加公益活动,每人一天,每天两人,则不同的选派方法共有
A.60种 B.48种 C.30种 D.10种
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.已知直线a,直线b,且a∥b,a上有5个点,b上有4个点,则以这九个点为顶点的三角形个数为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.在平面直角坐标系xOy上,平行直线x=n(n=0,1,2,…,5)与平行直线y=n(n=0,1,2,…,5)组成的图形中,矩形共有
A.25个 B.36个 C.100个 D.225个
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)下列等式正确的是
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 A是组合数公式;
两者不相等,故D错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
126
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.男女学生共有8人,从男生中选取2人,从女生中选取1人,共有30种不同的选法,其中女生有______人.
2或3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.高二(1)班共有35名同学,其中男生20名,女生15名,今从中选出3名同学参加活动.
(1)其中某一女生必须在内,不同的选法有多少种?
解 从余下的34名学生中选取2名,
∴不同的选法有561种.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)其中某一女生不能在内,不同的选法有多少种?
∴不同的选法有5 984种.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)恰有2名女生在内,不同的选法有多少种?
∴不同的选法有2 100种.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(4)至少有2名女生在内,不同的选法有多少种?
∴不同的选法有2 555种.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(5)至多有2名女生在内,不同的选法有多少种?
∴不同的选法有6 090种.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.现有8名青年,其中有5名能胜任英语翻译工作,有4名能胜任德语翻译工作(其中有1名青年两项工作都能胜任).现在要从中挑选5名青年承担一项任务,其中3名从事英语翻译工作,2名从事德语翻译工作,则有多少种不同的选法?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 可以分三类:
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.从10名大学毕业生中选3人担任村长助理,则甲、乙至少有1人入选,而丙没有入选的不同选法的种数为
A.28 B.49 C.56 D.85
√
解析 依题意得,满足条件的不同选法的种数为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.某餐厅供应饭菜,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种.现在餐厅准备了5种不同的荤菜,若要保证每位顾客有200种以上不同的选择,则餐厅至少还需准备不同的素菜品种____种(结果用数值表示).
7
解析 设餐厅还需准备x种不同的素菜.
即x(x-1)≥40.
又x≥2,x∈N*,所以x的最小值为7.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.在同一个平面内有一组平行线共8条,另一组平行线共10条,这两组平行线相互不平行,它们共能构成______个平行四边形,共有____个交点.
1 260
80
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.将标号为1,2,…,10的10个球放入标号为1,2,…,10的10个盒子里,每个盒内放一个球,恰好3个球的标号与其在盒子的标号不一致的放入方法种数为
A.120 B.240 C.360 D.720
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.某次足球赛,共32支球队参加,它们先分成8个小组进行循环赛,决出16强(每队均与本组其他队赛一场,各组一、二名晋级16强),这16支球队按确定的程序进行淘汰赛,最后决出冠、亚军,此外还要决出第三名、第四名,问这届世界杯总共进行了多少场比赛?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 可分为如下几类比赛:(1)小组循环赛:每组有 =6(场),8个小组共有48场;
(2)八分之一淘汰赛:8个小组的第一、二名组成16强,根据赛制规则,每两个队比赛一场,可以决出8强,共有8场;
(3)四分之一淘汰赛:根据赛制规则,8强中每两个队比赛一次,可以决出4强,共有4场;
(4)半决赛:根据赛制规则,4强每两个队比赛一场,可以决出参加决赛的两支球队,共有2场;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(5)决赛:两支球队比赛1场确定冠、亚军,4强中的另两支球队比赛1场决出第三、四名,共有2场.
综上,由分类计数原理知,共有48+8+4+2+2=64(场)比赛.
本课结束
